中学受験を目指す小学4年生で「容器に水を入れる問題がよく分からない」応用問題を解きたい」という方、お任せ下さい。
この記事では、東大卒講師歴20年の図解講師「そうちゃ」が容器に水を入れる「容積」の問題を基本から分かりやすく説明します。
記事を読んで例題を解けるようになれば、容積の問題が苦手ではなくなっているでしょう♪
目次(クリックでジャンプ)
水量の求め方
中学受験では主に4年で立方体直方体の単元で一緒に学習します。
水の量
公式
直方体の容器に入った水の量は「方体」の体積の求め方と同じです。
●直方体の体積=(たて×横×高さ) cm3
●立方体の体積=(一辺×一辺×一辺) cm3

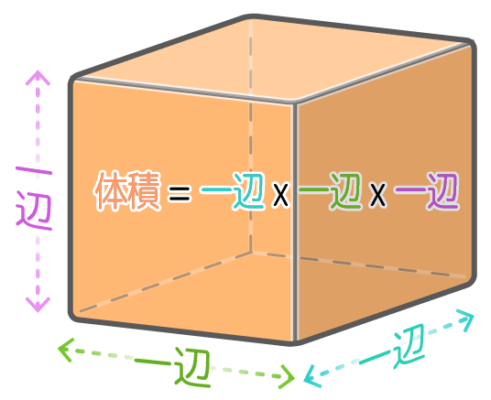
ただ、容器に入った水は「たて」と「横」は変わらずに「高さ(深さ)」だけがふえていくので、「たて×横(=底面積)」という言葉を使い、「底面積×深さ」と表します。
四角柱の体積は「底面積×高さ」でしたが水の量では「底面積×深さ」にします。
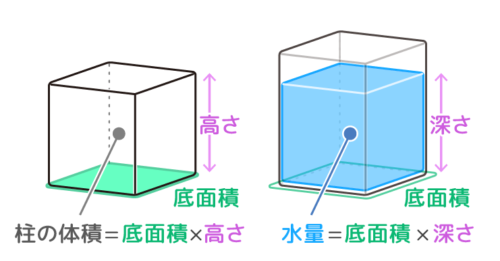
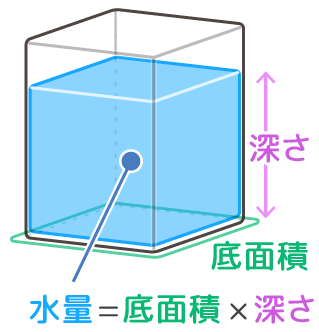
「底面積」「深さ」と合わせて「水量の公式」とします
①水量=底面積×深さ
②深さ=水量÷底面積
③底面積=水量÷深さ
水の量の単位
水そうの問題では水量を表すのに「L(リットル)」を使うことがあるので、「cm3」と「L」の関係を思い出しておく。
1L=10dL=1000cm3
(例)12L=12000cm3
1dL=100cm3
(例)6dL=600cm3
確認テストをどうぞ
底面40cm×60cmの水そうに30cmの深さまで水を入れると何Lか
→( 水量=底面積×高さ=40×60×30=72000cm3=72L )
一辺30cmの立方体に18Lの水を入れたときの深さ
→( 底面積30×30=900、水量=18L=18000cm3なので、深さ=18000÷900=20cm )
横の長さが15cmで、7.2Lの水を入れると深さが40cmになる水そうのたての長さ→( 7.2L=7200cm3、底面積=7200÷40=180cm2、たて=180÷15=12cm )
容積
厚みを考える
容器などの中に入る体積を「容積」といいますが、上の水量と同じで求め方は立方体直方体の体積と変わりません。
ただ、容器には厚みがあるので、外側から計った寸法(外寸)と内側から測った寸法(内寸)が異なります。そして容積の計算には内寸を使わないといけません。
例えば、図のような容器があった場合、外寸は「 cm× cm× cm」ですが、内寸は厚みの1cm(または2つ分2cm)小さくしないといけないので、
((図))
内寸は「 cm× cm× cm」になるので、容積は になります。
❶外側から計った寸法(外寸)と容器の厚みから、内側から測った寸法(内寸)を求める。
❷内寸を使って、「たて×横×高さ」を計算する。
容器自体(材料)の体積を求める
→「外のり」の体積ー「内のり」の体積
水の深さの問題
基本問題
水量→深さ・底面積
深さ・底面積→水量
密閉容器を倒す
水がこぼれないように密閉して立てた直方体の容器に水を入れてから倒す(はじめと別の面を床に付ける)
水の量は変わりませんが、底面積が変わるので、水の深さが変わります。
水を移す問題
全部移す
ある容器に入った水を別の容器に移す問題→水の量が変化しないことに注目して解く
一部を移す
別の容器に移した水と元の容器に残った水の高さが同じになった場合
→2つがつながった容器(底面積も和になる)を考えて、まず移転後の高さを出してしまう。
物を沈める(全水没)問題
モノを水中に沈めるのには、完全に水面下に沈める「全水没」と一部が水上に出る「半水没」の2通りがあり、ここでは「全水没」のみを扱います。
(半水没に興味がある人は関連記事「モノを沈める」を見て下さい)
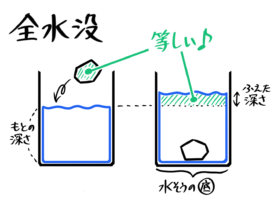
◆全水没(モノが水面から出ていない場合)
(公式) 物の体積=底×増えた深さ
その他の問題
受験小5以降で学習する、水に関するその他の(応用)問題はこちら
「密閉容器の横転」「解法容器の傾けと水こぼれ」「物体の水没(半水没はコチラ)」「注水とグラフ問題」
 爽茶
爽茶●
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
