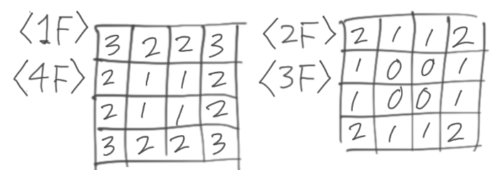「立方体・直方体って何?」という低学年の方から、「入試で出る応用問題を解きたい」という小6中学受験生の方へ
この記事では立方体と直方体(合わせて「方体」)について東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。
記事を読めば、「方体」の基本から応用まですっきり理解できるでしょう。
目次(クリックでジャンプ)
「方体」の性質

このサイトでは立方体と直方体を合わせて「方体」と呼んでいます。
「方」=直角という意味なので、方体=「直角で出来ている立体」ということです。
方体の名称
立方体
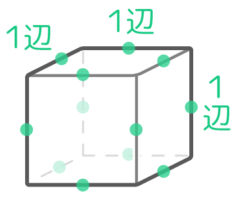
同じ大きさの正方形(面)が6つ組み合わさった立体で、同じ長さの「辺」12本が直角に交わり、合計8個の「頂点」がある。
身近なもので例えると、サイコロの形ですね。
同じ長さの辺が12本
頂点が8個

よく見ると
美しさに溢れている
直方体
長方形が6つ組み合わさって出来た立体で、向かい合う面は同じ形になっている。部屋の中で周りを見回すと必ず1個はあるでしょう
頂点が8個

面の平行と垂直
2つの同じ向きの面を「平行」、直角に交わる2つの面の関係を「垂直」という。
方形は直角で出来た整った立体なので、2つの面の関係は「平行」と「垂直」しかありません

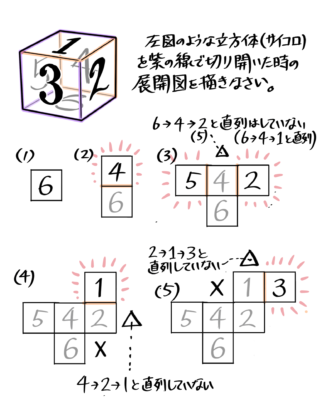
図のようなサイコロの場合で考えると、「1」と裏にある「6」(サイコロの目は裏表の和が7になる)が平行です(「5」と「2」、「3」と「4」も平行)。
それ以外の関係、例えば「1」と「5」、「3」と「5」などは垂直です
方体の寸法
三つの長さ
たて・よこ・高さの3つの長さを持つ(立方体はたて・よこ・高さが同じで「一辺」と表現する)
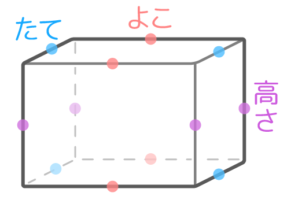
タテ、ヨコ、タカと呼びましょ
方体=四角柱の一種
勉強が進むと、立体図形として「柱」「すい」が登場します。方体は「柱」の中の「四角柱」の一種です。
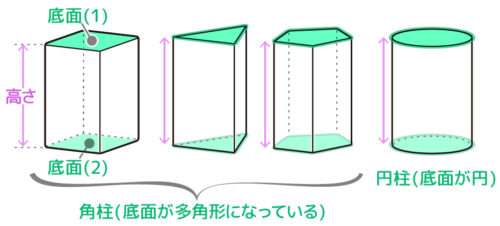
詳しくは関連記事「柱体まとめ」を見て下さい。
リボンの問題(後述)
プレゼントを送る時、箱にリボンをかけることがありますね。あのリボンの長さなどを出す問題です。
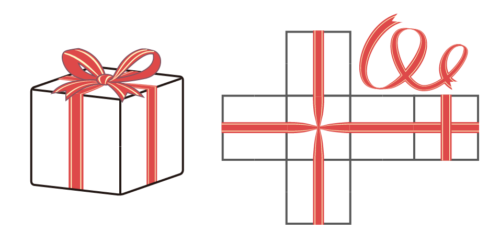
テキストによっては「立/長方体の構成」の直後に扱っていますが、「展開図」を学習してからの方が分かりやすいので、少し後ろで説明します。
方体の展開図
立方体を展開する
基本の展開図
立方体
身近なもの例えば(紙で出来た)サイコロを分解するのをイメージしてみます。
サイコロの目が「1」から「6」まで6個あるのを思い出せばで6面に分解できると分かる。
いろいろな展開の方法があるが、基本はこれ。立方体の上の面と下の面をこちら側に起こして、ぐるっと一回り残った面を一箇所切る
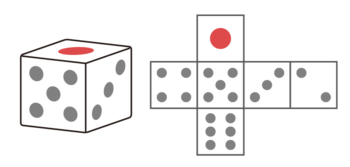
上下の面(1と6)をつける
あるいはマインクラフト風に遊んでもよいでしょう
その他の展開図
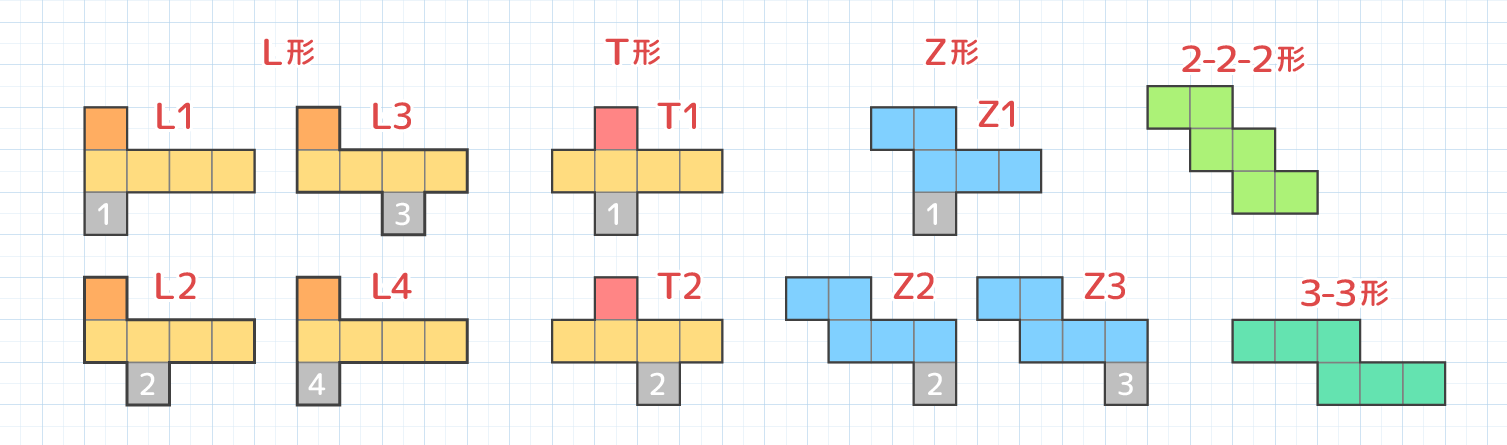
方体の展開図は全部で11種類あります。
「そうちゃ式」では以下のように分類をおすすめしています。
上で見た展開図は「三段型Tバリエの1番目」になります。
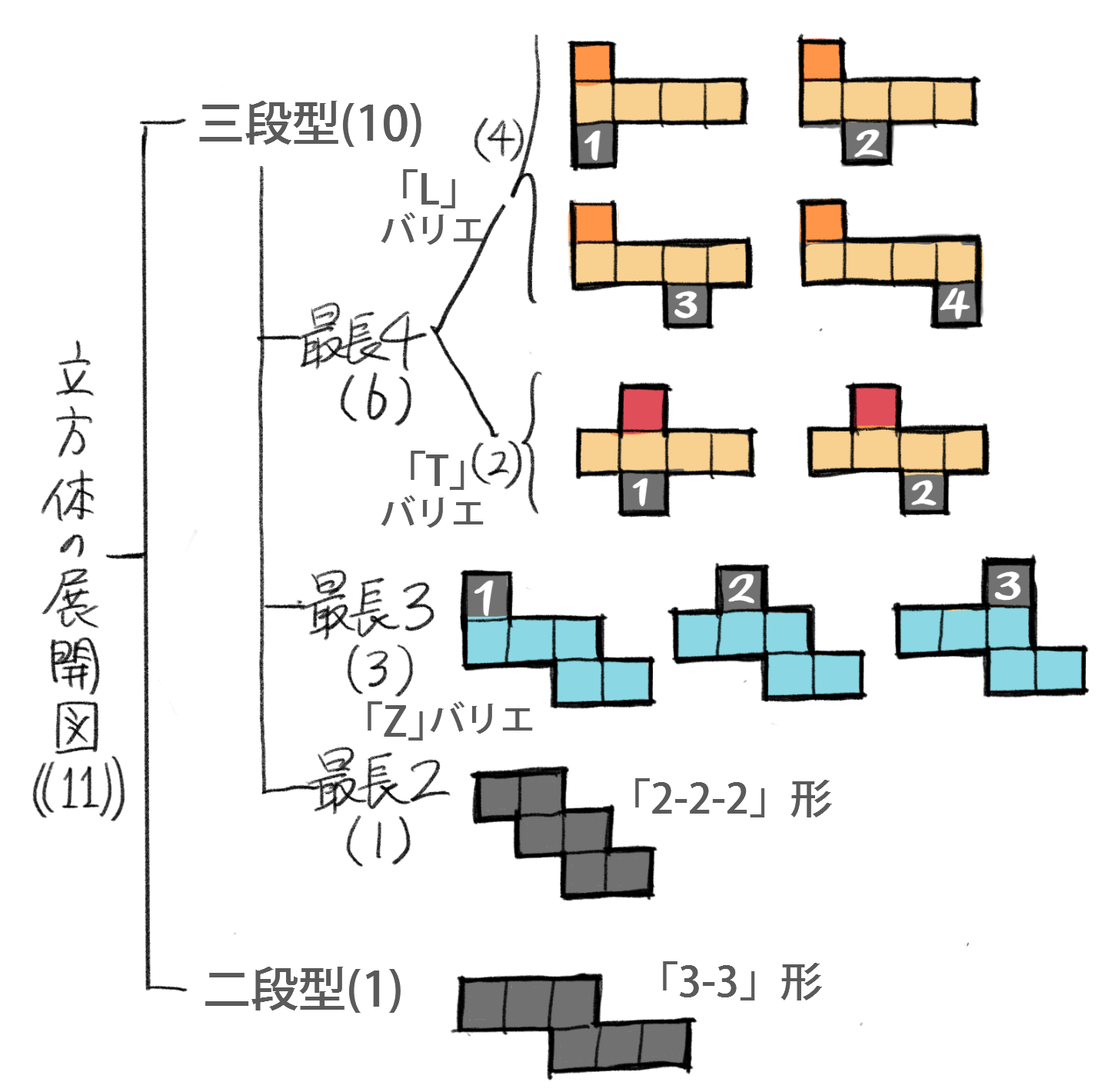
三段Z形(3つ)、2-2-2形、3-3形
禁則
問題を解く際には「禁じられた形(禁則)」を覚えておくのが良い
覚え方
横方向になぞって三段になるのが合計10パターン、二段になるのが1パターン。
三段になるもので最長の並びが4個のパターンは、L形の下に1個付くバリエーションが4パターン、逆T形の下に1個付くバリエが2パターン
三段で最長の並びが3個のパターンは3-2の並び(Z型)の上に1個付くバリエが3パターン(これが覚えにくいな…)
三段で最長の並びが2個のパターンは2-2-2の1パターンのみ
直方体の展開図
開き方
6個の面に「前」「上」などの文字が書いてあるつもりで展開する
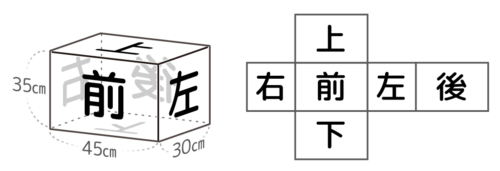
があると考えると分かりやすい。
長さの関係
もとの直方体には「縦」「横」「高さ」の3種類の長さしかなく、展開図にも3種類の長さが何回もでてきます。
つまり、展開図上には同じ長さの辺がたくさんあります。
例えば図のような直方体を「T1」形の展開図にすると、同じ長さ(同じ記号)の辺がこんなにたくさんあります
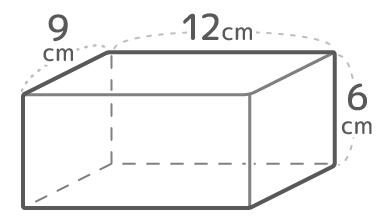
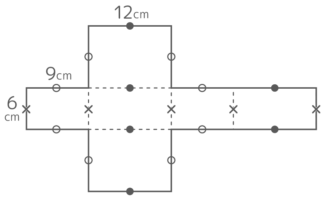
長さが同じになるのは
①組み立てた時にくっつく2つの辺(同じ記号の辺)は同じ長さになる。さもないと組み立てられない!
②面(長方形)で向かい合っている2つの辺は同じになる
この2つです
2つのルールにしたがって記号をどんどん移していくイメージで、展開図に長さが等しい記号を書き込みましょう。これがこの後問題を解く「自分に対するヒント」になります♪
では展開図の書き方が分かったところで、いろいろな問題を解いてみましょう
展開図の問題
指定辺で切り開く問題
立方体を切り開く辺を指定されて、展開図を書く問題
3-0:指定辺で切り開く

解答
コツは「切り開く」辺でなく「つながったまま」の辺に注目すること

つながった辺(橙)に注目
この状態から、6の面からスタートして面をつなげていきます。
つながっている面が一方向に連続しているかを見て、連続しているなら展開図上も連続させます。
連続していない場合、連続する方向の左右どちらかに曲がります。そのときはどちらか一方はXの事が多いです。(下の図の(4)に注目)
「三段三連」の「2型」が出来ました。
練習問題
長さの決定
長さを出す練習問題
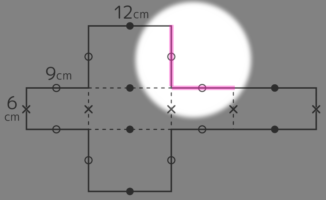
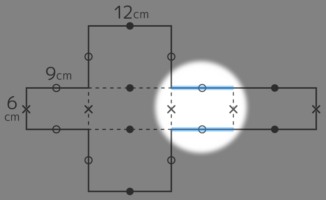
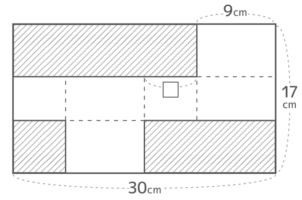 右図のように縦17cm横30cmの紙から斜線部分を切り取って直方体の展開図を作る。□に入る数字を求めなさい
右図のように縦17cm横30cmの紙から斜線部分を切り取って直方体の展開図を作る。□に入る数字を求めなさい
[予4下4基本2′]
同じ長さに印をつけると9cm(○)があちらこちらに見つかります。ここから●の長さを出せば終了です
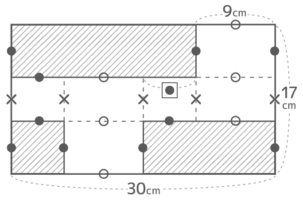
紙全体の横幅に注目すると30cmは○2つ(9×2=18cm)と●2つの合計と等しいので、18+●●=30 で●●=30-18=12 ●=12÷2=6cm と分かり、□=6cm
ちなみに、縦幅17cmは●2つ(6×2=12cm)とX1つの合計と等しいので、12+○=17 で ○=17-12=5cm と分かる
よって出来上がるのは辺の長さが5cm,6cm,9cm の直方体になる
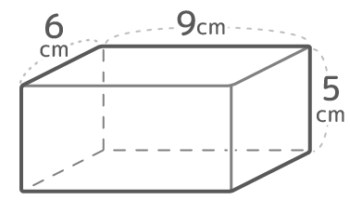
練習問題(応用)~三和算を使用
[6オープン2022-12]
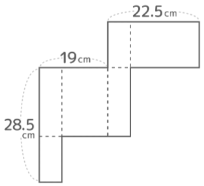 右図のような展開図を組み立ててできる直方体の辺の3つの長さを小さい方から書きなさい
右図のような展開図を組み立ててできる直方体の辺の3つの長さを小さい方から書きなさい
3つの長さを「S(short)」「M(middle)」「L(long)」とおいて、2つづつの和だけ分かる3つの数の問題(三和算)として解く
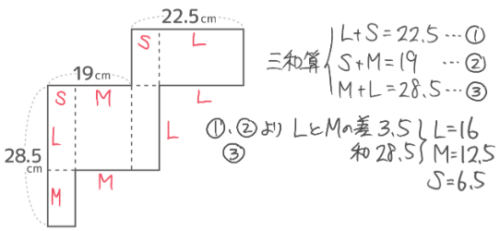
小さい方から 6.5cm,12.5cm,16m と求められる
リボンの問題

贈り物の箱に綺麗な色・デザインのリボンを巻いてもらうことがありますね♪
ここでは色やデザインでなく(当たり前ですが…)リボンの「長さ」を考えます。
立方体の場合
リボンを貼り付けた状態で(!)立方体を切り開くことをイメージする(展開図と言います)。
これを観察すると…使ったリボンの長さは「一辺の長さ」8個と「結び目に使う長さ」の合計、と分かります。
例えば、20cmの立方体に結び目50cmでリボンを巻くと、必要な長さは?
→20×8+50=210cm
確認テスト1
30cmの立方体に330cmのリボンを巻く時、結び目に使う長さは何cmか?
→330-(30×8)=90cm
反対に、リボンの長さから一辺を出すことも出来ます。
確認テスト2
立方体に270cmのリボンを巻いて結んだところ、結び目の長さが70cmになった。この立方体の一辺は何cmか?
→(270-70)÷8=25cm
直方体の場合
直方体は三種類の長さがあるので、それぞれの長さを何回使ったかを数えます。
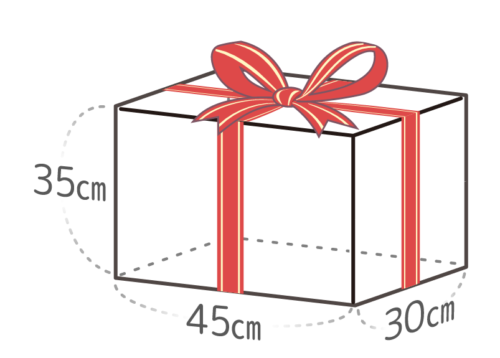
たてx2+よこx2+高さx4+結び目の長さ
使ったリボンの長さは「たて」2個、「よこ」2個、「高さ」4個と「結び目に使う長さ」の合計と分かります。
あとは立方体と同じように考えます。
例えば、たて cmよこ cm高さ cmの直方体に結び目 cmでリボンを巻くと、必要な長さは?
→ cm
確認テスト1
たて cmよこ cm高さ cmの直方体に cmのリボンを巻く時、結び目に使う長さは何cmか?
→ cm
確認テスト2
たて cmよこ cm高さ cmの直方体に cmのリボンを巻いて結んだところ、結び目の長さが cmになった。この直方体の高さは何cmか?
→ cm
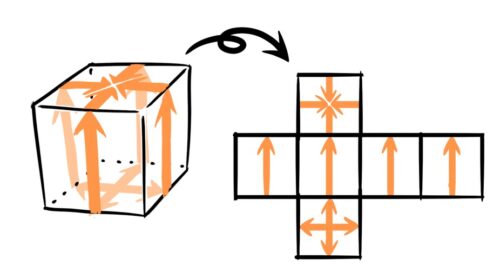
面の向き(平行と垂直)
ある面と平行・垂直な面を判断したい場合、その面から四方に広がる矢印を書き、矢印が集合する面が平行で、あとの面は垂直になる。
この矢印を書けば、11パターンの展開図どれでも大丈夫です。
例題
[作成中]頂点の決定
見取り図と展開図から、頂点を決定する問題
(例題の画像)
イメージして決めるのが難しい場合、いくつかのルールを組み合わせて考える
①対岸の2点
➁2面の対角線
➂ぐるっと一周
(例題)
面の決定
[作成中]サイコロ問題

サイコロを転がして、目に関する質問に答える。
その他の問題
最短距離
展開図上で直線で結んだ距離が最短距離になります。
(図)
塾では5年生で習いますが予習したいという人は関連記事「直角三角形と相似」を見て下さい。
方体の計量

方体の体積
基準立方体
縦横高さがすべて1cmの立方体(図)の体積を1cm3(立方センチメートル)と決めます。この立方体は体積を決める基準になるので「基準立方体」と名付けましょう。
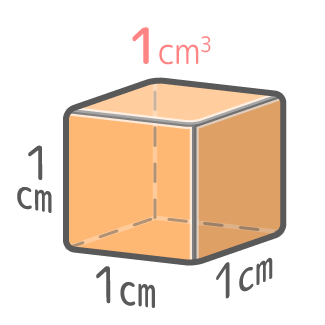
様々な直方体の体積は、この「基準立方体」を何個含んでいるかで決まります。
体積の公式
たとえば「たて1cm横3cm高さ1cm」の直方体は縦方向に3個の「基準立方体」を含んでいるので、3cm3です。
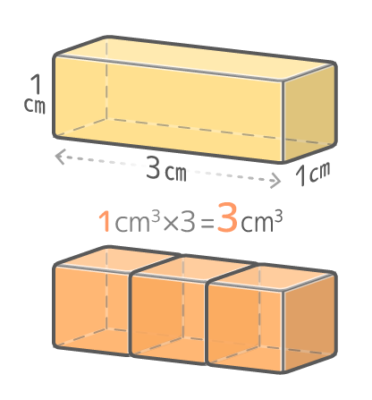
また「たて2cm横3cm高さ1cm」の直方体は縦方向に2個、横方向に3個で合計2×3=6個の「基準立方体」を含んでいるので6cm3です。
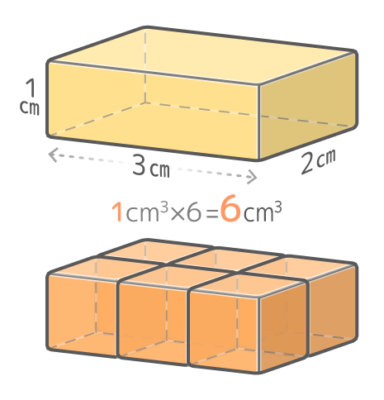
さらに「たて2cm横3cm高さ4cm」の直方体は、たて方向に2つ、横方向に3つ、高さ方向に4つで合計で2x3x4=24個の「基準立方体」を含んでいるので、体積は24cm3になります。
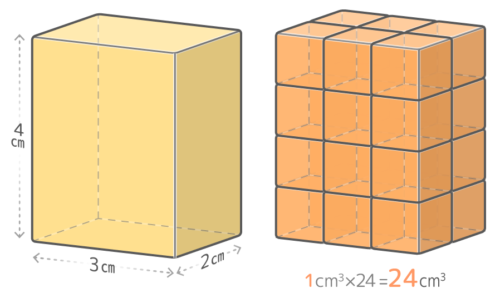
この理屈は縦横高さが小数になっても変わらないので、結局直方体の体積は単純に「たて×横×高さ」で決まります。
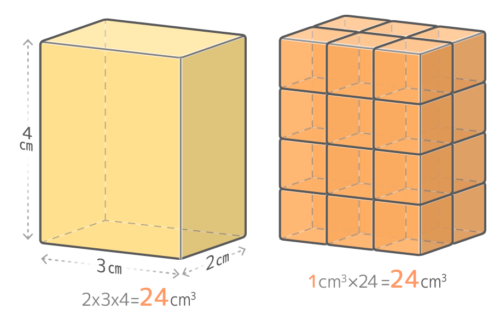
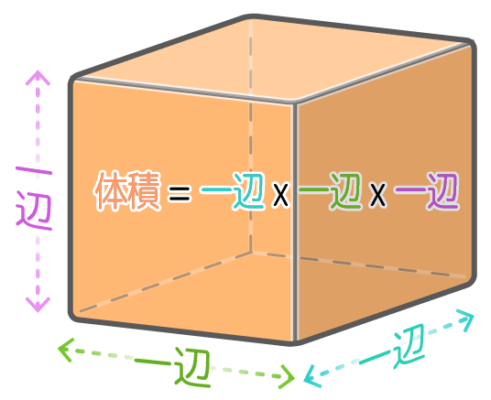
また、立方体の場合は、たて・横・高さが同じなので、「たて×横×高さ」を「一辺×一辺×一辺」と表現します。
●直方体の体積=(たて×横×高さ) cm3
●立方体の体積=(一辺×一辺×一辺) cm3

確認テストをどうぞ
たて5cm,横2cm,高さ6cmの直方体の体積
→(5x2x6=60cm3)
一辺3cmの立方体の体積
→(3x3x3=27cm3)
体積からの逆算
体積が分かっている方体の長さを求める
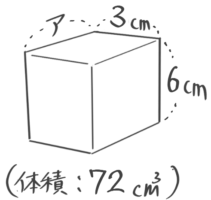
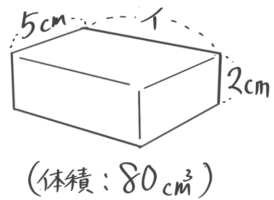
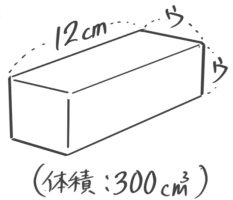 ア、イ、ウの長さを求めなさい[予4下4類題1追加]
ア、イ、ウの長さを求めなさい[予4下4類題1追加]
公式を使って逆算を作ります
(1)アx3x6=72 つまり アx18=72 という関係があるので、これを逆算として解くとア=72÷18=4cm
(2)5xイx2=80 つまり イx10=80 という関係があるので、これを逆算として解くとイ=80÷10=8cm
(3)12xウxウ=300 つまり 12x(ウxウ)=300 という関係があるので、これを逆算として解くと(ウxウ)=300÷12=25なので九九の「5×5=25」を思い出してウ=5cmと求められる
練習問題(2023年度中に補充予定)
容積(水)
容器などの中に入る体積を「容積」といいます。容器には厚みがあるので、外側から計った寸法(外寸)と内側から測った寸法(内寸)が異なります。そして容積の計算には内寸を使わないといけません。
❶外側から計った寸法(外寸)と容器の厚みから、内側から測った寸法(内寸)を求める。
❷内寸を使って、「たて×横×高さ」を計算する。
容積の問題には「容積を求める」「容器自体の体積」「水の移動」「容器の傾けと溢れる水」「物を沈める」等があります。
詳しくは「容積の問題」を見て下さい
体積の単位
m3とcm3の関係
1辺1m3の立方体
1m3=1m×1m×1m=100cm×100cm×100cm=1000000cm3
メートル系は長さの単位で増える0の個数の3倍の0が増える
●1cm3=1cm×1cm×1cm
=10mm×10mm×10mm=1000mm3
●1m3=1m×1m×1m
=100cm×100cm×100cm=1000000cm3
まとめると
__
__
(体積)
(0が1個増える)
↓↓↓
1cm3=1000mm3
(0が1×3個増える)
(0が2個増える)
↓↓↓
1m3=1000000cm3
(0が2×3個増える)
0が3倍増えるリズムを覚える。
計算問題
以下の計算に答えなさい[予4下4基本1′]
(1)6m3=□cm3
1m3=1000000cm3なので6m3=6000000cm3
(2)0.07m3=□cm3
1m3=1000000cm3なので小数点を6つ右にずらします
=70000cm3
70000cm3と分かります
(3)30000cm3=□m3
1000000cm3=1m3なので小数点を6つ左にずらします
=003cm3
0.03m3
(4)0.003m3-2400cm3=□cm3
0.003m3=3000cm3 なので、
=3000cm3
0.003m3-4000cm3=3000cm3-2400cm3=600cm3
容積など他の単位も知りたい人は姉妹サイトの「単位の総まとめ」を見て下さい
方体の表面積
表面積の求め方
「表面積」の求め方には2つの考え方があります
考え方1(6方向から見る)
前・右・上の三方向から見た図の面積を合計して2倍します。
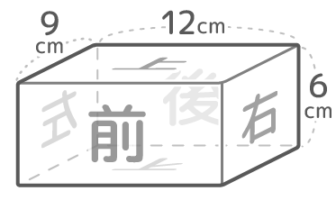
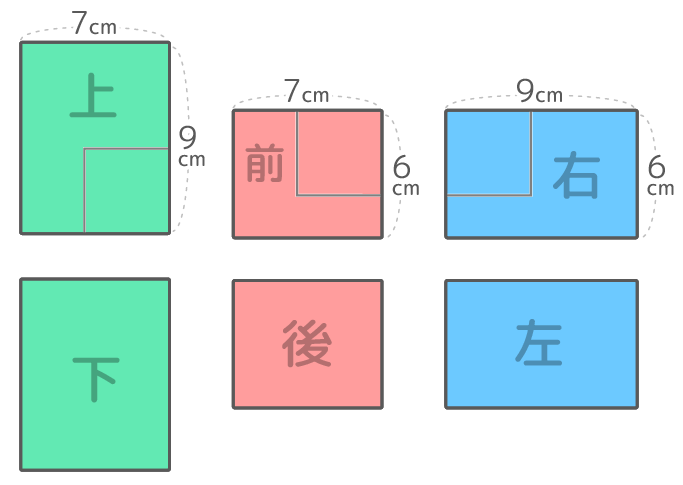
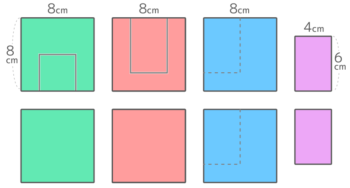
上図のような縦9cm,横12cm,高さ6cm直方体(説明しやすいように面に名前を入れてあります)の「上・下を向いている面」を緑で、「前・後ろを向いている面」を赤で、「右・左を向いている面」を青で塗り分けます。
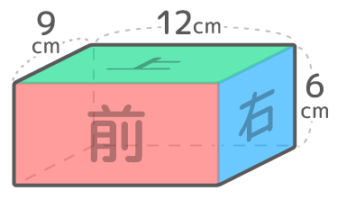
この着色した状態で「上から」「前から」「右から」直方体を見るとこうなります。

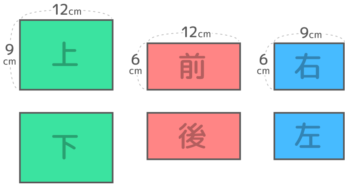
{(9×12)+(6×12)+(6×9)}x2=234×2=468cm2
上から見た形の面積は(9×12)=108cm2で下から見ても同じ形・面積になので、上と下から見た形の面積は合計で(9×12)x2 です
同様に、前と後ろから見た形の面積は(6×12)x2、右と左から見た形の面積は(6×9)x2 です。
表面積はこれら6方向からみた面積の合計なので、(9×12)x2+(6×12)x2+(6×9)x2=(108+72+54)x2=234×2=468cm2になります。
このように直方体の表面積は{(縦x横)+(横x高さ)+(高さx縦)}x2で求めることができます
立方体の場合は、同じ形の正方形が6個あるので表現が少し変わります(無理に覚えなくても良い)。
◆直方体の表面積
={(縦x横)+(横x高さ)+(高さx縦)}x2
(例)たて9,よこ12,高さ6の直方体の表面積
→{(9×12)+(6×12)+(6×9)}x2=234×2=468
◆立方体の表面積
=(1辺x1辺)x6 :6方向どこから見ても正方形
考え方2(展開図)
「表面積」は「展開図の面積」と同じです。
そこで、上で学習したやり方で「たて3cm横5cm高さ4cm」直方体の(「T1」形の)展開図を書くとこうなります(四角柱と考えた展開図)。
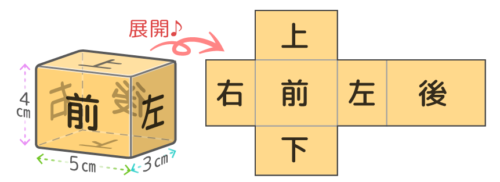
この展開図に長さを書き込んでみると、それぞれの長方形の面積が分かります。
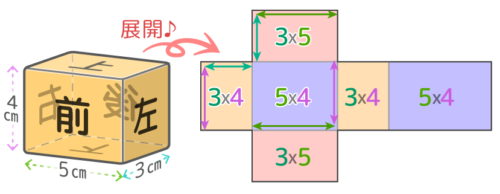
この展開図は「3×4」「3×5」「5×4」の3種類の長方形が2つずつあるので、合計すると {(3×4)×2}+{(3×5)×2}+{(5×4)×2} で、まとめると、{(3×4)+(3×5)+(5×4)}×2 となります。
さっきの「6方向から見る」考え方と計算式は同じになりました。
●直方体の表面積
={(たてx横)+(横x高さ)+(高さxたて)}x2 cm2
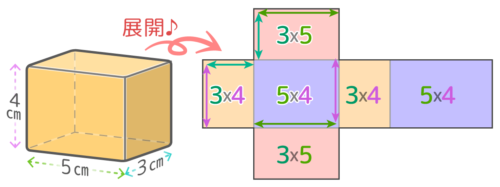
(例)たて3,横5,高さ4の立方体の表面積
={(3×4)+(3×5)+(5×4)}×2=47×2=94cm2
●立方体の表面積
=(一辺×一辺)×6 cm2
実際に問題を解いてみましょう
練習問題(計算)
練習問題(逆算)
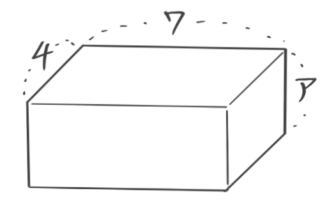 右図の直方体の表面積が122cmのとき以下の問いに答えなさい
右図の直方体の表面積が122cmのとき以下の問いに答えなさい
[予4下4例題2追加]
(1)アの長さは?
(2)直方体の体積は?

直方体の組み合わせ(複合体)

ここからは、いくつかの直方体を組み合わせたり引いたりしてできる立体(直方複合体)に関する問題です
角が欠けた方体
豆腐の端っこをつまんだように角(かど)が欠けた、こんな立体です。
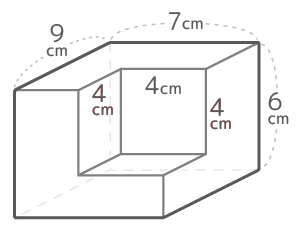
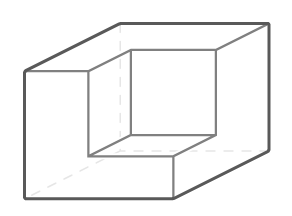 右図は縦9cm横7cm高さ6cmの直方体から1辺4cmの立方体を削り取った立体です。
右図は縦9cm横7cm高さ6cmの直方体から1辺4cmの立方体を削り取った立体です。
この立体の体積と表面積を求めましょう[予4下4基本3′]
体積
問題文にある通り、この立体は直方体から立方体を引いたものです
なので、直方体の体積から立方体の体積を引くのが簡単で良いでしょう
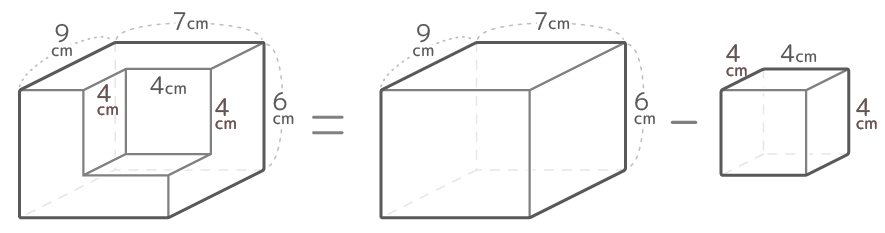
例の場合は、(9x7x6)-(4x4x4)=378-64=314cm3 になります。
表面積
直方体の表面積を出す考え方(その1)がありましたね


{(9×12)+(6×12)+(6×9)}x2=234×2=468cm2
あれと同じ様に考えます。
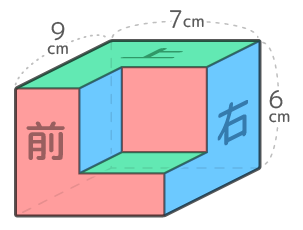
上下前後左右からみるとただの長方形なので計算は簡単です
{(7×9)+(7×6)+(9×6)}x2=159×2=318cm2 になります。(ただの直方体の表面積と同じになりました)。
練習問題
計算
右図の立体は立方体から直方体を切り取ったものです。[予4下4例題3′]
(1)体積を求めなさい
(2)表面積を求めなさい
逆算
柱状の複合体
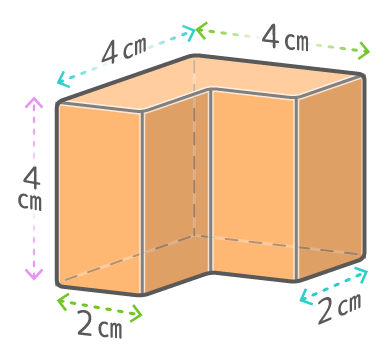
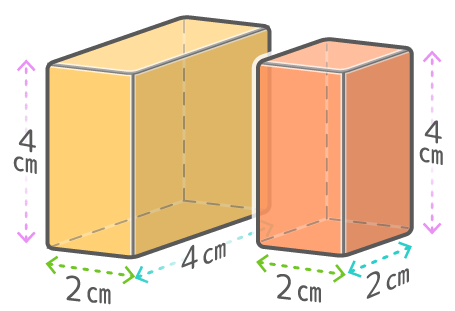
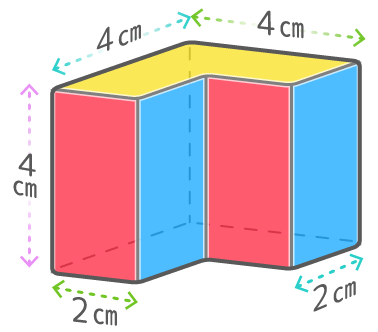
2つの直方体を同じ長さの部分で組み合わせた立体
体積
いくつかの直方体に分けて体積を出して合計して出すのが基本
例の場合は、「たて4,横2,高さ4の直方体」と「たて2,横2,高さ4の直方体」に分けられるので、体積の合計は(4x2x4)+(2x2x4)=32+16=48cm3になります。
柱として求める
共通する長さを「高さ」と考えると、高さと垂直な面は「底面」と考えることができる。
柱の体積は「底面積x高さ」なので、底面を (2×4)+(2×2)=12 と求めてから、12×4=48と計算できる。
かけ算が1回ですむので計算が単純になります。
これからは、コチラの考え方で求めます
★共通する長さ(高さ)と垂直な面を「底面」とみる
体積=「底面積」x「高さ」
表面積
上の「欠けた方体」と同様に前・右・上の三方向から見た図の面積を合計して2倍します。
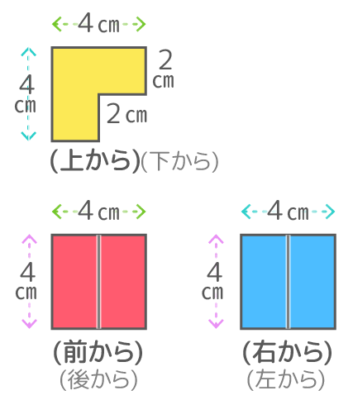
上のL字形の柱の「上・下を向いている面」を黄色で、「前・後ろを向いている面」を赤色で、「右・左を向いている面」を青色で塗り分けます。
この着色した状態で「上から」「前から」「右から」立体を見るとこうなります。
上から見た形の面積は(4×2)+(2×2)=12cm2で下から見ても同じ形・面積になります。
前と後ろから見た形の面積は4×4=16、右と左から見た形の面積も16です。
表面積はこれら6方向からみた面積の合計なので、12×2+16×2+16×2=(12+16+16)x2=88cm2になります。
練習問題
練習問題
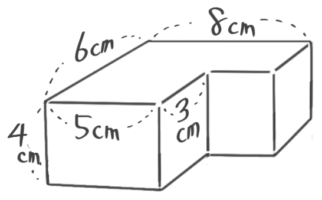 右図の立体は、2つの直方体を組み合わせたものです。以下の問いに答えなさい(SSHT2023)
右図の立体は、2つの直方体を組み合わせたものです。以下の問いに答えなさい(SSHT2023)
(1)体積は何cm3か
4cmを「高さ」、上面(下面も同じ)のL字形を「底面」と見る。
底面の面積は6×5+3×3=39cm2なので、体積は39×4=156cm3
(2)表面積は何cm2か
6方向から見て合計すると
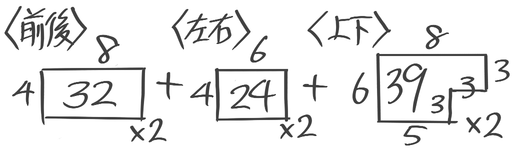
={(4×8)+(4×6)+(6×8)}x2=95×2=190cm2
底面が前を向いているタイプ
Y[予4下4基本4]
逆算問題
その1
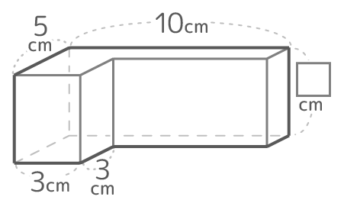 右の立体は直方体を2つ組み合わせたもので体積が174cm3である。□は何cmか
右の立体は直方体を2つ組み合わせたもので体積が174cm3である。□は何cmか
Y[予4下4例題4′]
□を高さ、上面のL字形を底面とみて底面積を求めると29cm2なので
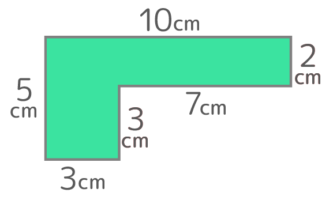
29x□=174 という関係が成り立つ。
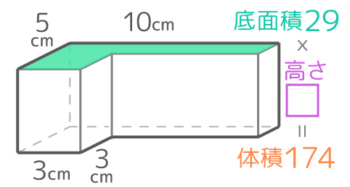
この逆算を解いて□=174÷29=6cm
その2
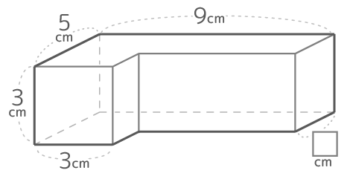 右図の直方体を組み合わせた立体の体積が99cmのとき、□は何cm3か
右図の直方体を組み合わせた立体の体積が99cmのとき、□は何cm3か
Y[予4下4例題4’追加]
3cmを高さ、上面のL字形を底面とみると
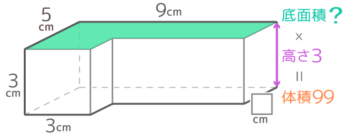
底面積?は 99÷3=33cm2で、
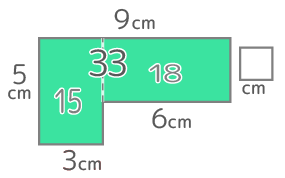
底面積を左右に区切ると左が3×15なので、□={33-15}÷6=18÷6=3cmと求められる
中央が欠けた・凹んだ複合体
体積は今までと同様に求められるが、表面積を求めるときは工夫が必要になる。
例題
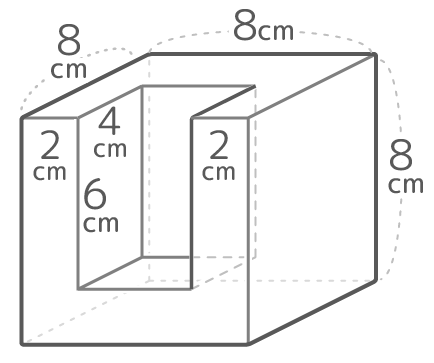 右図の立体は立方体から直方体を切り取った形です。(2023SSHT)
右図の立体は立方体から直方体を切り取った形です。(2023SSHT)
(1)体積を求めなさい
8x8x8の立方体から4x4x6の直方体を引けば良いので、512-96=416cm3
(2)表面積を求めなさい
今まで通りに6方向からみると、8×8の正方形の面積が6個分で8x8x6=384cm2
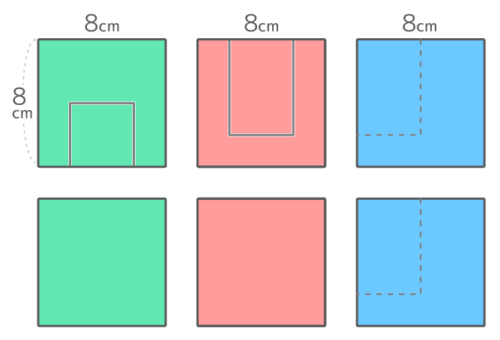
ですが、6方向からは隠れて見えない面(紫:4×6)2個分=48cm2を足さないといけない
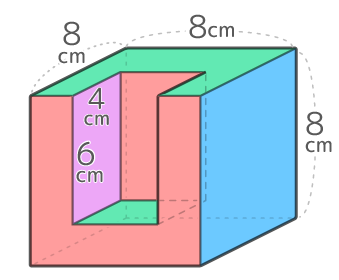
全部で384+48=432cm2になります。
練習問題(23.5.1作成中)
角が柱状に欠けた方体
先程の2つのタイプを組み合わせたような問題です。
((図))
体積
欠けていないと仮定した全体の体積(A)から欠けた柱状部分の体積(B)を引きます。
((図))
表面積
角が欠けた柱状の複合体
これも組み合わせです。
体積
表面積
階段状の立体
例えば図1のような立体です(階段のように見えます)。
(図)
同じものをもう一つ準備して組み合わせると直方体になります(図2)。
((図))
体積
組み合わせてできた直方体の体積を÷2すると、元の階段状の体積が出ます。
表面積
小立方体の集合体
小さな立方体が集まって大きな形を作っている場合の問題です。
このサイトでは「立方集合体」と呼びます。
個数問題
定まっている場合
見取り図から立方体の個数を出すような問題です。
((図))
イメージできない場合は、階層(1F,2F,3F…)ごとの上面図を書いて数えます。
定まっていない場合
正面から見た図と横から見た図しかない場合は、個数が正確に決まりません。
そういう場合に一番多い場合(最大値)や少ない場合(最小値)を求める問題です。
詳しい解説を読みたい・問題を解きたい人は「立方体の集合体」を見て下さい。
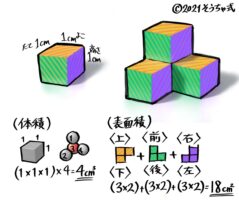
体積
集合体の体積を求める問題
集合体の体積=小立方体1個の体積×立方体の個数
個数が分かれば簡単
(練習問題作成中)
表面積
集合体の表面積を求める問題
標準
6方向(上下前後左右)から見た面積を合計する。
上と下、前と後、左と右から見た面積は同じなので、上前左から見た面積を合計して2倍すれば良い
簡単に計算できる。
応用
6方向からでは見えない面がある場合は、それらの面を追加で加えないといけない
((図))
詳しい解説を読みたい・問題を解きたい人は「立方体の集合体」を見て下さい。
色塗り後に解体
小立方体が集合した大立方体に色を塗った後、もう一回バラバラにして塗ってある面を数える問題
階層ごとに塗ってある面を集計すれば確実
例題
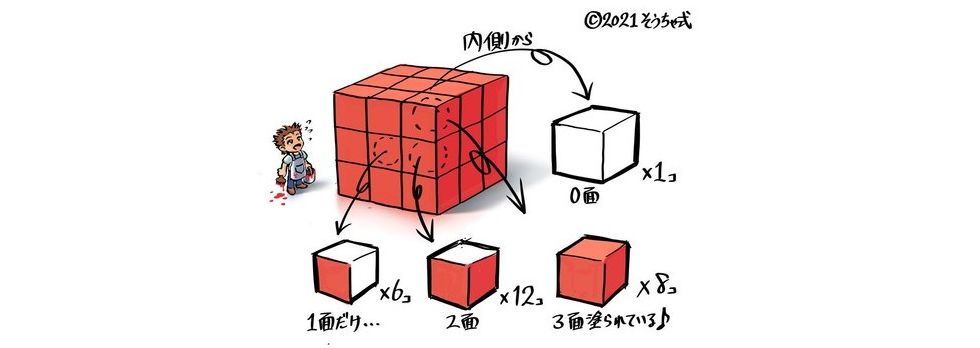
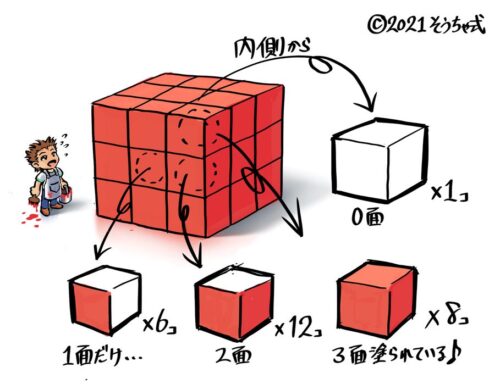
小さな立方体を図のように積み上げて大きな立方体を作り、この表面に色を塗った後、再びバラバラにした。
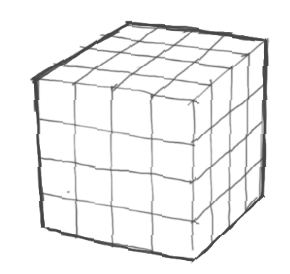
(1)塗ってある面が3つある立方体は何個か?
(2)塗ってある面が2つある立方体は何個か?
(3)塗ってある面が1つの立方体は何個か?
(4)1面も塗ってない立方体は何個あるか?
コツ
4階建てのビルと見て、1階から4階までをバラバラに書き一つ一つに塗られている面数を書き込みます。
数えて合計すると、3面:8個,2面:24個,1面:24個,0面:8個と分かります
詳しい解説を読みたい・問題を解きたい人は「立方体の集合体」を見て下さい。
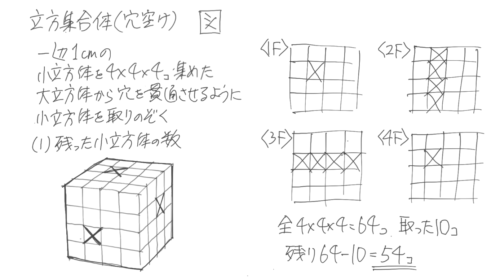
くり抜き
貫通する穴を作るように大立方体から小立方体を取り除く問題
個数問題
残った小立方体の個数を調べるときは、階層ごとの図の取り除いた箇所に「X」をつけていくと簡単
詳しい解説を読みたい・問題を解きたい人は「立方体の集合体」を見て下さい。
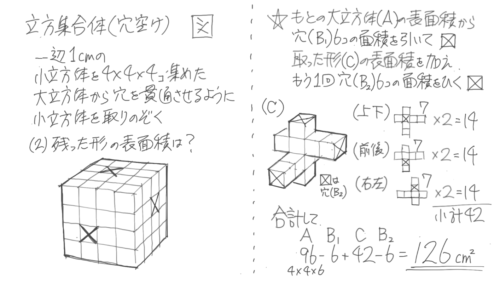
表面積
残った形の表面積を求める問題。
穴に石こうを流し込んで「型」をとるつもりで、穴の形を考える。
この形を利用すれば計算で求めることができる。
詳しい解説を読みたい・問題を解きたい人は「立方体の集合体」を見て下さい。
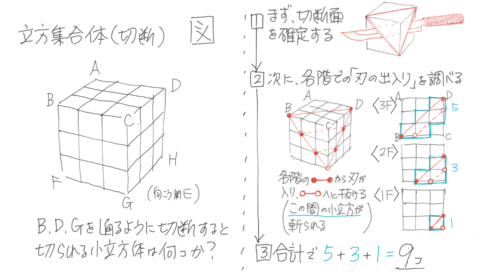
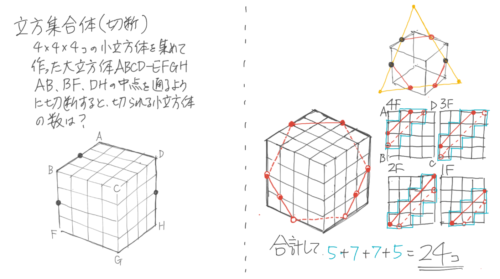
切断
小立方体が集まった大立方体や大直方体を切断して、斬られる(斬られない)立方体の個数を求める問題
コツは、各階での刃の「出入り」を記入すること
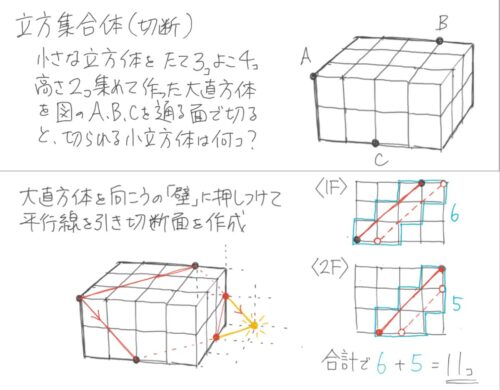
一番単純な例
各階の天井から刃が入ってきて、床に抜けていくイメージ
切り口を考える
指定点が同一平面上にない場合は、壁に押し付けて切り口を確定する必要がある
立方体の切断を復習したい人は「方体の切断」を見て下さい。
直方体の場合
直方体の場合も同様に解く
詳しい解説を読みたい・問題を解きたい人は「立方体の集合体」を見て下さい。
次のステップへ
 爽茶
爽茶オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。