[作成中]中学受験】四角形のまとめ。分類・公式から等積変形まで

 

色々な四角形(復習)

方形

((図))

4つの角が全て直角の四角形。長方形は向かい合う辺(対辺)の長さが等しくなり、正方形は全ての辺の長さが等しい。

平行四辺形

((図))

向かい合う辺(対辺)が2組とも平行になっている四角形。

対辺は長さも等しくなり、向かい合う角(対角)も等しい

台形

((図))

1組の対辺だけが平行になっている四角形。

ひし形

((図))

4つの辺の長さがすべて等しい四角形。

その他の四角形

((図))

以上の特徴をまったくもっていない四角形。名前が無いと困るので、このサイトでは「凡四辺形」と呼びます。

四角形の角度

一般ルール

四角形の内角の和は360度。四角形の中には三角形が(4-2)2つあるので180×2

外角の和も360度。これは全ての多角形に共通

台形の角度

一辺が平行な台形では、足すと180度になる2組の角度に分けることができる。

((図))

平行四辺形・ひし形の角度

向かい合う角度(対角)が等しいので、足すと180度になる2種類の角度しかない。

((図))

長方形・正方形の角度

全ての角度が等しく90度になる

それぞれの図形について詳しく知りたい・問題を解きたい人は「正方形長方形のまとめ」「平行四辺形のまとめ」「台形のまとめ」「ひし形のまとめ」を見て下さい。

四角形の面積(公式あり)

公式が決まっている四角形の面積等をまとめます。

正方形・長方形

周りの長さ

正方形のまわりの長さ＝一辺の長さ×4

長方形のまわりの長さ＝(たての長さ+よこの長さ)×2

面積

正方形の面積=一辺の長さ×一辺の長さ

長方形の面積=たての長さ×よこの長さ

正方形・長方形について詳しい説明を読みたい問題を解きたい人は参考記事「正方形長方形のまとめ」を見て下さい。

台形

台形の面積=(上底+下底)×高さ

それぞれの図形について詳しく知りたい・問題を解きたい人は「台形の性質と応用問題」を見て下さい。

平行四辺形

平行四辺形の面積=底辺×高さ

詳しく知りたい・問題を解きたい人は関連記事「平行四辺形の性質と応用問題」を見て下さい。

ひし形

ひし形の面積=対角線1の長さ×対角線1の長さ÷2

 

正方形はひし形と考えることもできる。

 

それぞれの図形について詳しく知りたい・問題を解きたい人は「ひし形の性質と応用問題」を見て下さい。

公式にない形の面積
～求積の工夫

公式にない形の面積を出す場合は工夫をしないといけません。工夫の仕方にはいくつかの方法があります。

A.公式で出せる図形の和や差にする
B.等積変形を使う
C.重なりを利用する
D.水平垂直を利用する

和や差に直す

公式で出せない四角形は、公式で出せる形を ➀足す ➁引く のどちらかで出せないか考えます。

図形の和

 

図形の差

 

等積変形を使う

等積変形の方法

 

例題

等積変形と図形の重複

図形重複の基本

 

例題

 

道の変形

基本パターン

 

クロス型

複合形

 

 

 

詳しい説明を見たい・問題を解きたい人は「求積の工夫」を見て下さい

その他の組合わせ図形

 

四角形の整理分類

これまで色んな四角形が出てきました。

習った順にならべると、「正方形・長方形」「平行四辺形」「台形」「ひし形」だったと思います。

ただ、四角形を分類する場合は「だんだん形を整えていく」という順番で整理すると特徴が理解しやすいです。

分類方法(整形順序)

何の特徴も無い四角形

↓一組の対辺が平行になる

台形(一組の対辺が平行)

↓もう一組も平行になる

平行四辺形(二組の対辺が平行)

↓四つの角が全て等しくなる　↓四つの辺が全て等しくなる

長方形(角が全て等しい)　ひし形(辺が全て等しい)

↓

正方形(辺も角も全て等しい)

図示

この分類(整形)では言葉の使い方に気を付けないといけません。

例えば「長方形」という言葉で連想するのはこういう形ですが

(横長長方形の図)

「長方形＝4つの角が等しい四角形」とすると、正方形も長方形の一種といえるのです。

同じように平行四辺形というと普通連想するのはこういう形ですが

(図)

「平行四辺形=二組の対辺が平行な四角形」とすると、「長方形」も「ひし形」も、そして「正方形」も「平行四辺形」に含まれます。

このような関係を図に表すと、このようになります(ベン図)

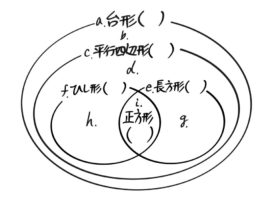
普通連想する「台形」はどこにあるか分かりますか？

aではなく、bの部分ですね。

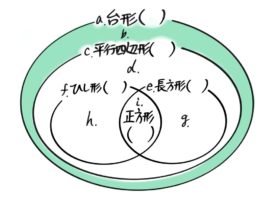
このbの部分を言葉で説明すると「一組の辺『だけ』が平行な四角形」になります。(「狭い意味での台形」とも言います)

同じように普通連想する(狭い意味での)平行四辺形を言葉で表現すると「二組の辺が平行だが、全ての辺や角が等しくは無い四角形」になります(狭い意味での平行四辺形)

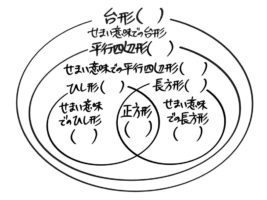
このように、分類の問題では表現に注意して下さい。

問題(集合算)

この分類を使った問題を解いてみましょう。「集合算」の一種です。

二組の辺が平行な四角形が14個ある。このうち4つの角が等しいものは5個、4つの辺が等しいものは7個、正方形は2個ある。ひし形でも長方形でもないものは何個あるか？

この問題では一番大きい集合が「平行四辺形」なので、ベン図はこうなります。

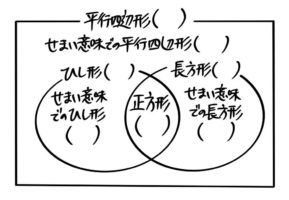
問題文を丁寧に読みながらカッコの中に数を入れていきます。答えになる箇所には「?」を書きます。

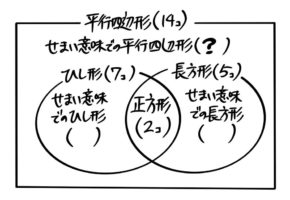
埋まっていない2箇所を求めると「？」以外の全箇所が埋まりました。これで準備終了です。

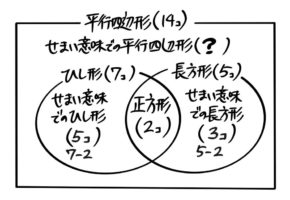
？は「全体」から「ピーナッツ型」を引けば出るので14-10=4個と分かります。

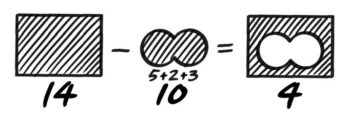
四角形の分類プリント

書き込み式のワークを作ってみました。よろしければ、どぞ

もっと詳しい説明を読みたい・問題を解きたい人は「四角形の分類」を見て下さい。

オススメ教材

次のステップへ

 

オリジナル教材のご案内

御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評！
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ

人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史　●時事問題(2025年)　●世界地図　●世界遺産
■仕事ニュートン算　■食塩水　■売買損益
★月の形　★電流　★水溶液/気体の性質

その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ