「正方形・長方形って何を勉強するの？」という小2から「入試問題に挑戦したい」という中学受験生の方まで、お任せ下さい！東大卒講師歴20年の図解講師「そうちゃ」が基本から応用まで分かりやすくまとめました。
下の目次から好きなところをクリックするとジャンプできます。
目次(クリックでジャンプ)
図形の基本要素(小2)
辺
真っ直ぐな線で囲まれた図形を「多角形(たかくけい)」と呼ぶ。
((色々な多角形))
特に、三本の線で囲まれているものは「三角形」四本の線で囲まれているものを「四角形」と呼ぶ。
((三角形と四角形))
頂点
辺と辺がくっついている(交わっている)ところを「頂点(ちょうてん)」と呼ぶ
三角形には頂点は3つ、四角形に頂点は4つある。
((三角形と四角形の頂点))
角度
頂点での辺と辺の開き具合を角度と呼ぶ。閉じた辺の角度は0°で、辺が開くと角度はどんどん大きくなって、360°になると元の0°に戻る
((0,45,90,135,180,270,360の図))
正方形・長方形の角度
(小2～小5)
「方形」の意味(小2)
正方形と長方形はどちらも「方形」という文字が入っています。「方形」は直角(90°)で出来ている四角形のことです。
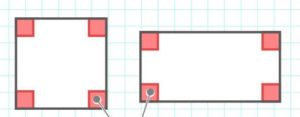
角度は4つとも90°
毎日見たり触ったりしている教科書・プリント・机・黒板、そして今見ている画面も！全部「方形」です。
内角と外角(小5)
内側の角度を「内角」、辺を伸ばして外にできる角度を「外角」という。
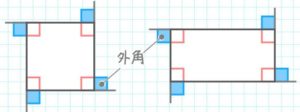
内側にあるのが内角、外側が外角
長方形や正方形は内角も外角も90°になっているのが分かります。
正方形と長方形は内角も外角も90°
内角と外角の和
内角と外角を足すと90+90=180°になっています。これは正方形・長方形だけでなく、他の四角形でも、三角形でも五角形でも(まとめて「多角形」と言います)内角と外角を足すと必ず180° になります。
多角形では必ず 内角+外角=180° になる
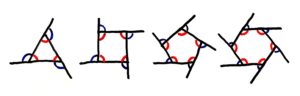
応用問題(中学受験)
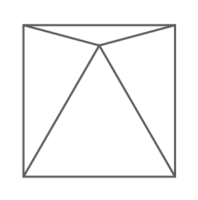
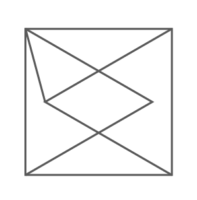
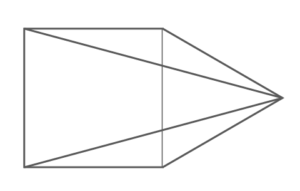
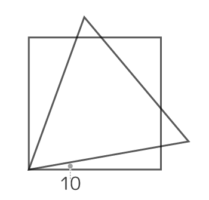
正三角形との組み合わせが聞かれます。正三角形の内角は全て60°であるのを利用します。
プリントダウンロード
著作権は放棄しておりません。無断転載引用はご遠慮ください。
方形のまわりの長さ
(小2～)
求め方
正方形と長方形のまわりの長さ
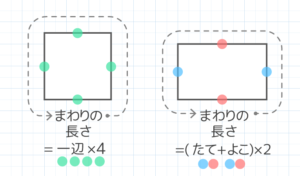
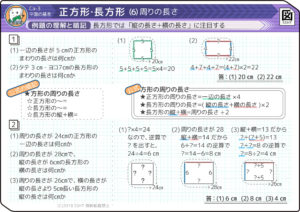
長方形のまわりの長さは「縦+横」セット２つ分になるのが重要です。
●正方形の周長=一辺の長さ×4
●長方形の周長=(縦+横)×2
→○長方形の縦+横=周りの長さ÷2
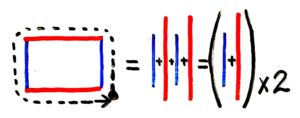
「長辺と短辺の和」に注目する
基本問題
(1)一辺が5cmの正方形のまわりの長さは？
→( 5×4=20cm )
(2)まわりの長さが36cmの正方形の一辺の長さは？
→( 36÷4=9cm )
(3)縦4cm横7cmの長方形のまわりの長さは？
→( (4+7)×2=22cm )
(4)縦8cmまわりの長さが26cmの長方形の横の長さは？
→( 縦+横=26÷2=13cm、13-8=5cm )
応用問題(中学受験)
まわりの長さが60cmで、縦が横よりも6cm長い長方形がある。横の長さは何cmか？
→( 縦と横の和=60÷2=30、差は6cmなので、和30差6の和差算になる。 )
→( 小=(和-差)÷2なので横=(30-6)÷2=12cm )
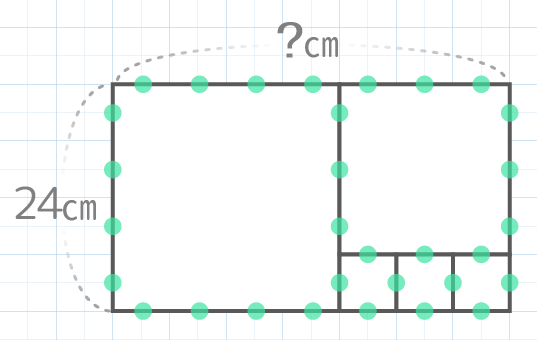
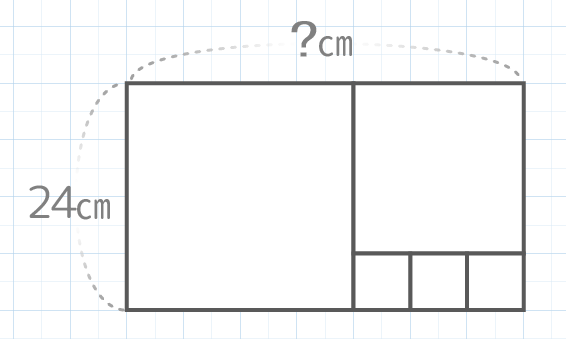縦の長さが24cmの紙からできるだけ大きな正方形を切り取るのを繰り返したら全て正方形に切り取れた。この長方形の横の長さはいくつか？
→(
プリントダウンロード
著作権は放棄しておりません。無断転載引用はご遠慮ください。
正方形・長方形の面積
(小4～)
面積の意味
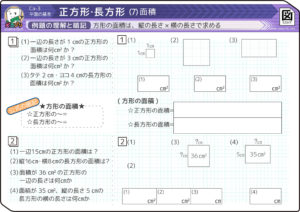
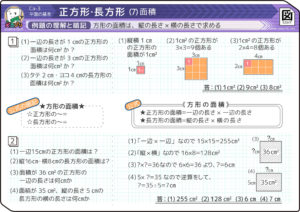
たて1cmよこ1cmの正方形の広さを「1cm2(へいほうせんちめーとる)」と決めます。これが面積の基準になります。
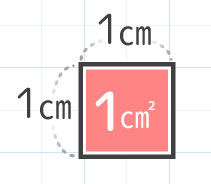
面積の基準になる「基準正方形」
(1cm2の大きさ)
公式
正方形や長方形の面積は「基準正方形」が何個入っているかで決まります。
例えば縦2cm横3cmの長方形には2×3=6個入っているので6cm2です(図)
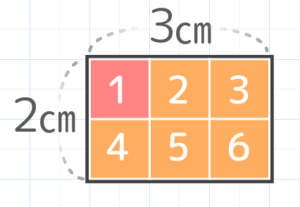
基準正方形が6個入っているので
面積は6cm2になる。
結局、縦と横の長さをかければ面積になります。理解したら公式として覚えてパッと言えるようにしましょう。
●1cm2の大きさ
=一辺1cmの正方形の面積
○正方形の面積=一辺×一辺
○長方形の面積=縦×横
基本問題
(1)一辺の長さが3cmの正方形の面積はいくつか？
→( 3×3=9cm2 )
(2)縦4cm横10cmの長方形の面積はいくつか？
→( 4×10=40cm2 )
(3)面積が49cm2の正方形の一辺の長さは？
→( 九九を思い出して7×7=49なので7cm )
(4)横の長さが7cm、面積が51cm2の長方形の縦の長さは？→( 51÷7=13cm )
プリントダウンロード
著作権は放棄しておりません。無断転載引用はご遠慮ください。
正方形のもう一つの公式～対角線を使う
正方形はひし形の一種と見る事もできます。例えば対角線(向かい合う角を結んだ線)の長さが2本とも4cmのひし形=正方形を例にとりましょう。
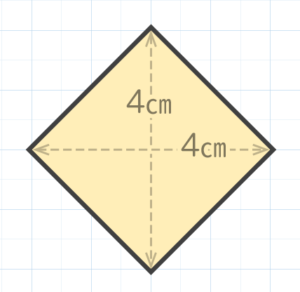
正方形でもあると言える
このひし形=正方形は、対角線の長さをかけ合わせた4×4=16のcm2の中にすっぽりおさまっていて、面積はその半分の8cm2になっています(図3)。
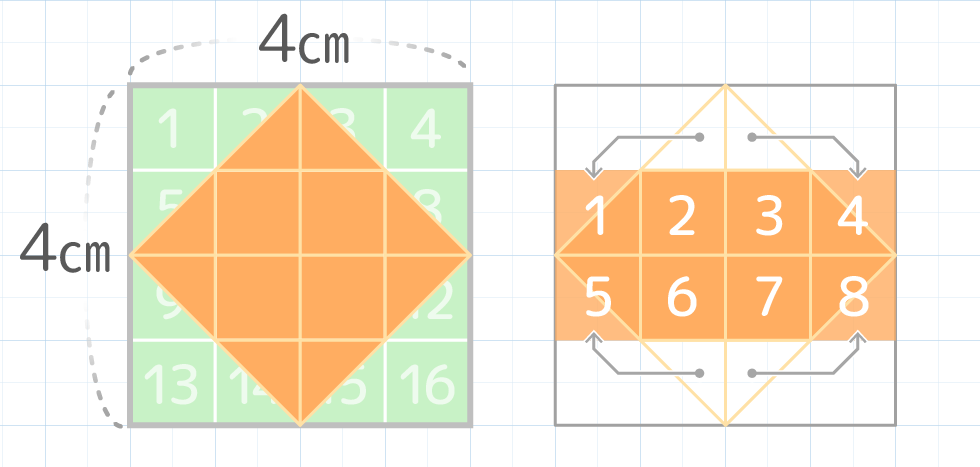
つまり、正方形の対角線の長さが分かっている場合は「対角線×対角線÷2」で面積を求めることもできるのです(これはひし形の面積の公式です)。
①長方形として～「一辺×一辺」
②ひし形として～「対角線×対角線÷2」
(1)対角線の長さが6cmの正方形の面積は？
→( 6×6÷2=18cm2 )
(2)面積が32cm2である正方形の対角線の長さは？
→( 対角線×対角線÷2=32 なので、対角線×対角線=32×2=64。2回かけて64になる数は8なので、対角線は8cm(試しに8×8÷2を計算すると64になりますね) )
これを利用した問題は中学受験でよく出題されます。詳しくは参考記事「四角形の種類」「円・おうぎ形」を見て下さい。
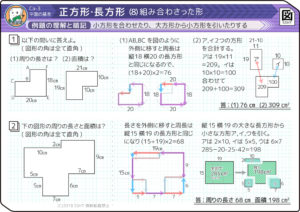
正方形・長方形の組合せ
(中学受験)
正方形・長方形を組み合わせた図形(複合体)の周囲の長さや面積を出します。今までの知識を総動員して解きます
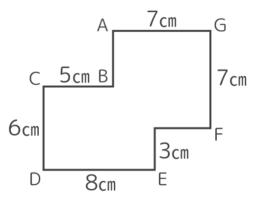
方形を組み合わせて作った「複合体」
まわりの長さ
考え方～「へこみ」を外側に移す
へこんでいる部分の長さを外側に「移す」と単純な長方形の周囲の長さと同じになることが多いので、それを利用すると簡単に解けます。
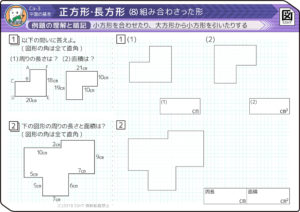
例えば、下のような図形の周りの長さを出す場合
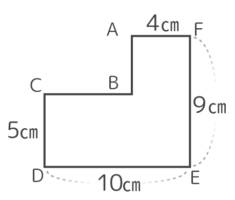
分からない長さがあります
書いていないABやBCの長さを出して、合計しても構いませんが…
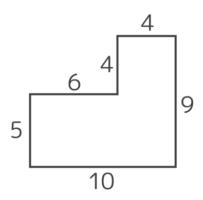
この長さを合計すれば周長になる。
凹んだ部分のタテの長さ(青)とヨコの長さ(赤)を外側に移すと、たて9cm、横10cmの長方形の周りの長さと同じになる(図2)のを利用すると、単純に(9+10)×2 で出せてラクです。
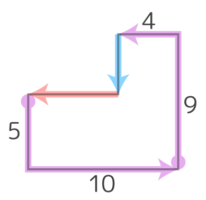
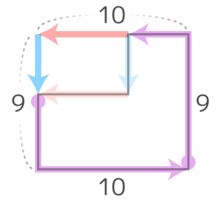
図形を囲む「大きな長方形」の
周りの長さと同じになる
形が複雑になればなるほど、このやり方で解く方がラクになります。
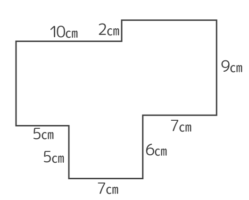
注意！外に移せない場合
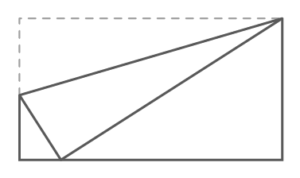
長方形を組み合わせた形の中には下の図のようなものもあります。
((図))
この形では、へこんだ部分の長さで外に移せないものが出てきます。
((図))
周りの長さは「大きな長方形」の周りの長さと「外に移せなかった長さ」を合わせたものになります。
((図))
移せない場合の見分け方
複合体を「大きな長方形をかじって作る」と考えます。へこんだ部分を外に移せるのは「頂点をかじった場合」です。
((図))
一方、外に移せないのは「頂点をかじらない場合」です。
((図))
これで2つの場合が見分けられますね。
((図1 図2))
では練習問題をどうぞ
練習問題
周りの長さは？
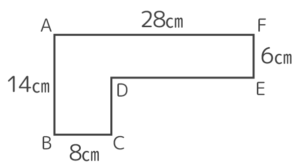→( 凹んだ部分の長さを外に移してできる大きな長方形の縦が14で横が28)
→( 周りの長さは(28+14)×2=84cm )
周りの長さは？
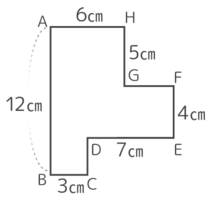
→( 大きな長方形の縦が12で横が3+7=10 )
→( 周長は(12+10)×2=44cm )
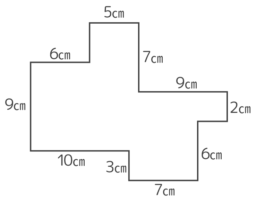
周りの長さは？
→( 大きな長方形の縦が9+6=15 )
→( 大きな長方形の横が5+7+7=19 )
→( 周長は(15+19)×2=68cm )
周りの長さは？
→( 大きな長方形の縦が7+2+6=15 )
→( 大きな長方形の横が6+5+9=20 )
→( 周長は(15+20)×2=70cm )
面積
考え方(大きな長方形から引く)
周りの長さの時と違って、面積を求める場合は全ての長さを出す必要があります。
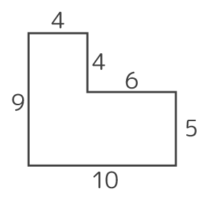
複合体の面積を出す方法は大きく2つあります。
1つ目は小さな方形をいくつか足す方法(A)で、2つ目は周りの長さを出すときに使った大きな方形から凹んだ部分の小さな方形を引く方法(B)です。
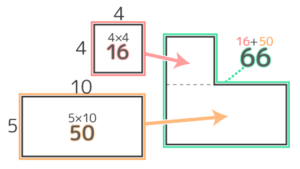
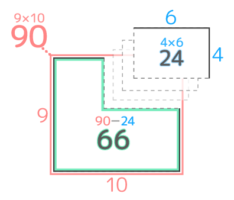
形が単純な場合はどちらの解き方でも良いですが、形が複雑になると「引く」方がラクに解けます。
練習問題(作成中)
面積は？
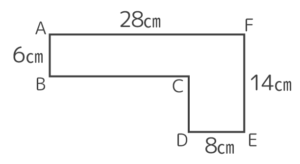→( 大きな長方形の面積が14×28=392 )
→( 凹んでいる小さな方形の面積が8×20=160 )
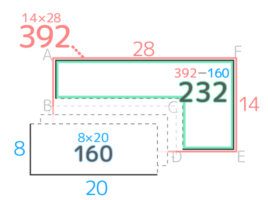→( もとの面積は392–160=232cm2 )
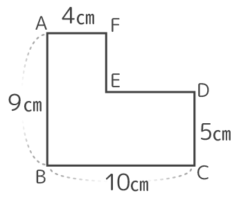
面積は？
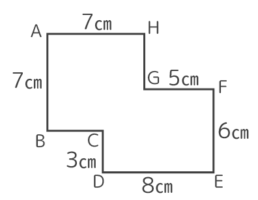→( 大きな長方形の面積が10×12=120 )
→( 左下の小さな方形の面積が3×4=12 )
→( 右上の小さな方形の面積が4×5=20 )
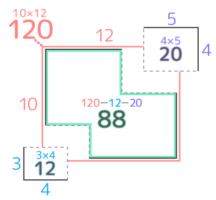→( もとの面積は120–12–20=88cm2 )
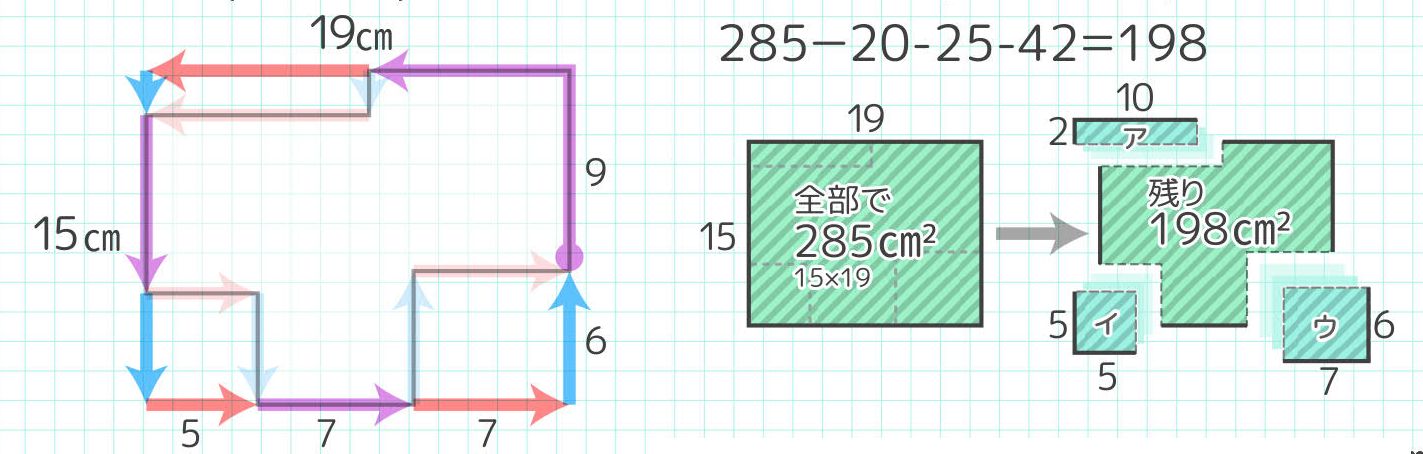
面積はいくつか？
→( 大きな長方形の面積が15×19=285 )
→( 左上の小さな方形の面積が2×10=20 )
→( 左下の小さな方形の面積が5×5=25 )
→( 右下の小さな方形の面積が6×7=42 )
→( もとの面積は285–20–25-42=198cm2 )
面積はいくつか？
→( 大きな長方形の面積が16×20=300 )
→( 左上の小さな方形の面積が6×4=24 )
→( 左下の小さな方形の面積が3×10=30 )
→( 右下の小さな方形の面積が6×3=18 )
→( 右上の小さな方形の面積が7×9=63 )
→( もとの面積は300–24–30–18–63=165cm2 )
プリントダウンロード
著作権は放棄しておりません。無断転載引用はご遠慮ください。
長方形の折り返し問題
(中学受験)
中学受験ではよく出題されます。一見難しそうですが、2つのコツをつかめば簡単に解けることが多いですよ♪
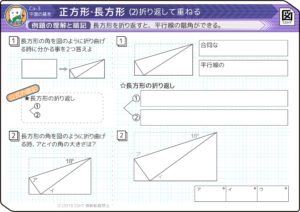
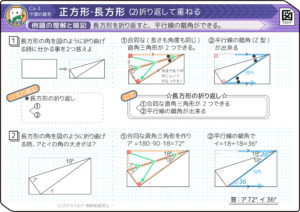
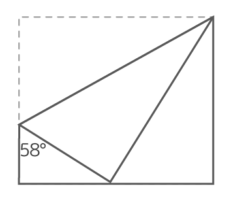
角を辺に重ねる折り返し
解き方・考え方
①図形の合同(同じ角度・長さ)を利用
②平行線の錯角が等しい事を利用
①折り返すと、角度と長さが同じ(合同)直角三角形ができます。問題文を読んだら自分で「同じ」印をつけましょう
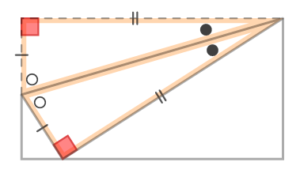
同じ角度と長さに印をつける
②さらに、長方形の向かい合う辺は平行なので、平行線の錯角を見つけて同じ印をつけます
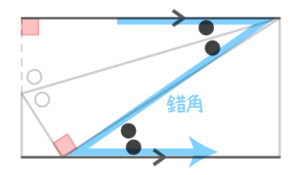
同じ角度に印をつける
「錯角」がよく分からない・忘れた人は参考記事「角度と平行線」内の「平行線が作る角度」を見て下さい。
練習問題
問題作成中
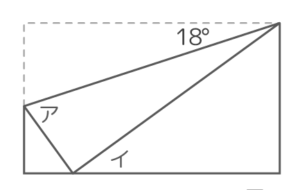
問題作成中
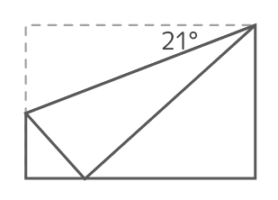
問題作成中
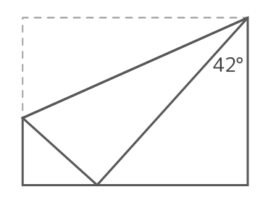
問題作成中
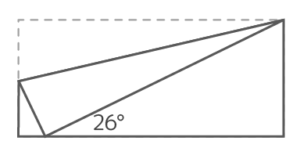
問題作成中
プリントダウンロード
著作権は放棄しておりません。無断転載引用はご遠慮ください。
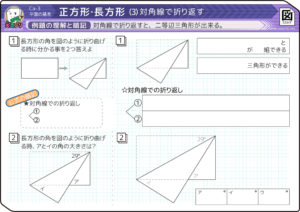
対角線での折り返し
特徴と考え方
①折り返した三角形の合同だけでなく、もう一つ合同な三角形の組ができる。
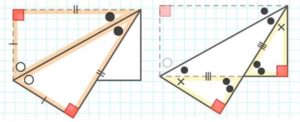
❷錯角も二組できて、二等辺三角形を作ります。
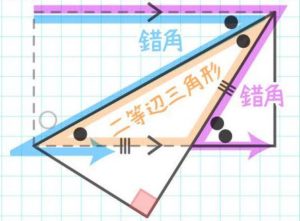
練習問題
プリントダウンロード
著作権は放棄しておりません。無断転載引用はご遠慮ください
はみ出る折り返し
特徴と考え方
練習問題
台形型の折り返し
特徴と考え方
練習問題
三角形の折返しについては「三角形のまとめ」内の「三角形の折返し」を見て下さい
性質公式のまとめ
正方形・長方形の性質・公式を確認テストの形でまとめました。
(作成中)
おすすめ教材
爽茶「小4までに…平面の図形センス」(シグマベスト)
「算数の基本問題4年(日能研)」
「塾技100 算数」(文英堂)
「分かりやすい！」と評判の
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。