[作成中]中学受験】四角形(台形・平行四辺形)の並行分割と面積比の問題

「面積比が苦手」という中学受験生の方へ

面積比というと「相似」を連想するかもしれませんが、実は相似を使う前の「底辺比と面積比」が半分以上を締めています。

ですから、相似を学習する前に「底辺比と面積比」に慣れておく必要があるのです。

そこで、この記事では東大卒講師歴20年の図解講師「そうちゃ」が相似を使って「いない」面積比を分かりやすく説明します。

記事を最後まで読んで理解できたら、いよいよ「相似比」に進んで下さい。

はじめに

今回の学習に必要な事柄に軽く触れます。

四角形の分割の2タイプ

当サイトでは、四角形を分割する面積比の問題を「並行分割」と「クロス分割」の2タイプに分けて考えます。

クロス分割

分割する線が交わっている(クロス)分割です(図右側)。この場合は「相似比」を使い、複雑になることが多いです。

並行分割

分割する線が交わらないタイプ(図左側)で、「相似比」を使わず「底辺比と面積比」を使います。

この記事では「並行分割」のみ説明します。「クロス分割」を学習したい人は関連記事「四角形のクロス分割」を見て下さい

三角形の底辺比と面積比

頂点から底辺を切るように分割すると、分割された底辺比と面積比は等しくなる

忘れた・よく分からない人は関連記事「三角形の底辺比と面積比」を見て下さい。

四角形の分類

四角形は何の特徴も無い「ただの四角形=凡四辺形(当サイトでの呼び方)」から完璧な四角形である「正方形」まで段階的に整形されます。

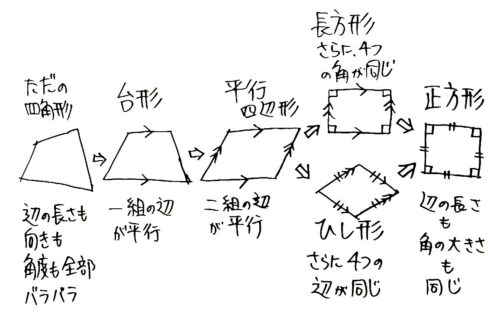
この種類をベン図にするとこうなります。

四角形の種類について詳しく知りたい・問題を解きたい人は関連記事「四角形まとめ」内の「四角形の種類」を見て下さい。

台形の分割

爽茶そうちゃ

はじめは「狭義の台形」の並行分割です。

対角線で分割

例えば台形ABCDを対角線BDで分割すると、高さが同じ2つの三角形△ABDと△DCBができる。

(図)

高さが同じ三角形の面積の比は底辺の比に等しいので、△ABDと△DCBの面積比は上底ADと下底BCの長さの比と等しくなる。

(図)

例えば、AD= cm,BC= cmのとき、△ABDと△DCBの面積比は上底AD:BC= : になる。

台形を見たら、まず対角線で分割してみること

底辺分割を加える

さらに底辺で分割すると、底辺の分割比と等しい比で三角形が分割される。

例えば、

(分割図)

この場合、3つの三角形の面積は : : になる。

(面積比を書きこんだ図)

利用問題

以上を利用して問題を解きます。

例題1(対角線以外での二分割から面積比を求める)

例題2(面積比から底辺の分割比を求める)

例題3(対角線以外での二等分)

平行四辺形の分割

台形よりも単純

対角線での分割

二等分されます。

平行四辺形の面積比の問題を見たら、まずは対角線で二等分してみるのをオススメします。

底辺分割を加える

利用問題

例題1(対角線以外での分割比)

例題2(逆向きの問題)

長方形・正方形

これらは平行四辺形の一種なので、平行四辺形と同じ解き方ができます。

(分割例の図)

(参考)凡四辺形の分割

台形ですらない四角形(凡四辺形とでも呼んでおく)を対角線で分割すると、対角線を共通の底辺とする、2つの三角形に分けられる。

この2つの三角形はもう一つの対角線を分けたものを含んでいます。

この分けられたもう一つの対角線がそろうように、180°回転させて左右を反転させると、三角形の高さは分けられた対角線の長さの比と等しいように見えますね？(本当は相似の知識が無いと分からないのですが、ここでは感覚でOK)

このように無名四角形を対角線で分けて出来る三角形の面積比は、もう一つの対角線が分けられた比と等しくなります。

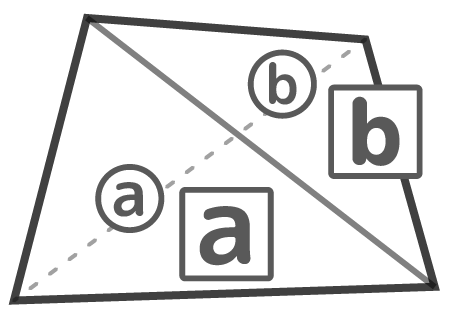
この性質は応用問題を簡単に解くのに非常に便利なので必ず覚えておきましょう。

オススメ教材

動画で学習したい人へ
「分かりやすい！」と評判のスタディサプリなら有名講師による図形問題の動画もありますよ♪
今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては？

オリジナル教材のご案内

御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評！
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ

人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史　●時事問題(2025年)　●世界地図　●世界遺産
■仕事ニュートン算　■食塩水　■売買損益
★月の形　★電流　★水溶液/気体の性質

その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ

歴史の点数を上げたい受験生と保護者の方へ

年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ

2023年度生徒さん募集

2023年度の生徒さんの募集を開始しました(対面授業の一次募集)

東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。

詳しくはコチラのページを御覧下さい

「図解サービスforSAPIX」のお知らせ

新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから

中学受験でお悩みの方へ

爽茶そうちゃ

いつもお子さんのためにがんばっていただき、ありがとうございます。

受験に関する悩みはつきませんね。
「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。

もしかしたら、自分だけで悩んでいると煮詰まってしまい、事態が改善できないかもしれません。講師経験20年の「そうちゃ」に相談してみませんか？対面/オンラインでの授業/学習相談を受け付けているので、ご利用下さい。

最後まで読んでいただきありがとうございました♪この記事があなたの役に立てたなら嬉しいです!