「図形と比」と聞くと「比?相似?底辺?」とやることが多くてイヤになっていませんか?あなたは一気に色々とやりすぎなのですよ。
実は「図形と比」には「相似」とは関係ないものが半分くらいあるのです。ですからまずは「相似」を使わないものだけを学習すると一気にラクになりますよ。
この記事では、東大卒講師歴20年の図解講師「そうちゃ」が三角形の面積比を「相似」を使わずに「底辺の比」などを使って解く問題の解き方を分かりやすく図解します。
記事を読めば「図形と比」のうち半分をマスターできるので、その後でゆっくりと「相似」を学習しましょう。
目次(クリックでジャンプ)
比(復習)
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
はじめに「比」を復習します。「分かるよ!」という人はジャンプして下さい♪
比例式
「A:B=C:D」の「A」「B」「C」「D」のうち分からない1つを出す方法(AとDを外項、BとCを内項と言います。)
外項
内項
内項
外項
内側2つが「内項」
A×D=B×C(外項の積と内項の積は等しい)を利用して、内項と外項のうちそろっている方の積を残りの数で割る。
例えば「7:5=2:?」の場合、内項がそろっているので内項の積5×2を残りの数7で割って?=107になります。
外項
内項
内項
外項
?=5×2÷7=107
詳しくは「比の基本」を見て下さい(姉妹サイトに移動します)
複数比のそろえ方
全体を2通りに分割する場合
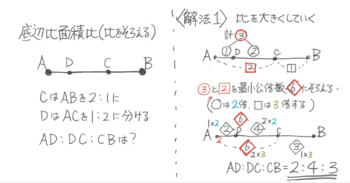
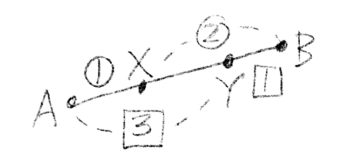
例えば線分ABについて、Xは全体を1:2にYは全体を3:1に分ける時に、AX:XY:YBを求める問題です。
大きく分けて2つの解き方があります。
解法A:比を大きくしてそろえる
Xは1:2に分けるので全体を3に、Yは3:1に分けるので全体を4に分けています。
3と4の最小公倍数は12なので、全体を12に分けると考えます。
Xは12を1:2に分けるので4:8に分けることに、Yは12を3:1に分けるので9:3に分けることになります。
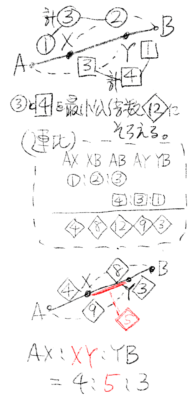
これでAX:XY:YBは4:5:3と分かりました。
解法B:全体を割合で分けていく
割合を思い出して全体を1と考えます。
XはABを1:2に分けるのでAXは13、XBは23になり、YはABを3:1に分けるのでAXは34、XBは14になります。
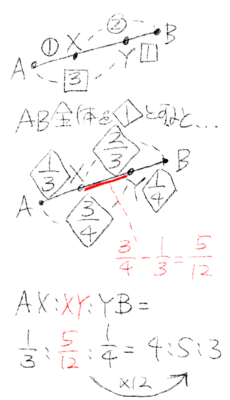
XYは34–13=512と分かるので、AX:XY:YB=13:512:14と分かります。
ここで分母(3,4)の最小公倍数が12なので、比を全部12倍して4:5:3になります。
一部を更に分割する場合
例えば線分ABがあってCはABを2:1にDはACを1:2に分ける時にAD:DC:CBを求める問題です。
((図))
こちらも2通りの方法があります。
比を大きくしてそろえる
細かく割合で分けていく
詳しくは「倍数算」を見て下さい(姉妹サイトに移動します)。
前提~等積変形
形が違っても、底辺と高さが同じなら面積も等しくなります(等積変形)
((頂点を移動した等積変形))
高さが等しい場合は、面積は底辺で決まります。底辺が2倍なら、面積も2倍になります。
((図))
このように、高さが等しい三角形の面積は、底辺に比例する。
基本1~頂点から切る
頂点から1回切り分け
△ABCのBCを1:2に分ける点Dをとり、頂点Aからハサミを入れてDに向かって切ります。
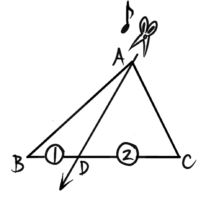
△ABCをADで切り分けた△ABDと△ADCは高さが等しく底辺の比が1:2になので面積の比も1:2になります。全体の面積は➀+②=➂になるので、これも書き込んでおきます(後で問題を解く時に役立ちます)。
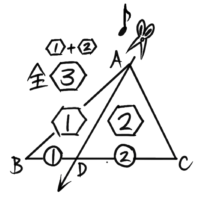
全体の面積3を書くこと
これが「底辺比と面積」の基本ルールです。
→頂点を通る線で切り分ける時、
底辺比と面積比は等しくなる。

(例)△ABCを、頂点Aから
BCを1:2に分ける点Dで切ると
△ABDと△ADCの面積比も1:2になる
比から面積を計算
先程の△ABCの面積が36cm2の場合、△ADCの面積は何cm2でしょうか?
比が書いてあれば分配算と同じ様に解けます。
全体➂=36なので、➀=36÷3=12、△ADC=②=12×2=24cm2ですね。
((図))
確認テスト
面積から比を逆算
先程の図で△ADCの面積が18cm2の時、△ABCの面積は何cm2でしょうか?
△ADC=②=18なので、△ABC=➂=18÷②×3=27cm2ですね。
((図))
確認テスト
頂点から何回か切る
2回以上分ける場合
レ型に2回切る
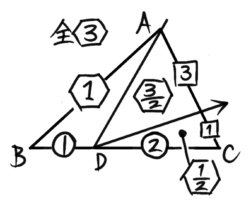
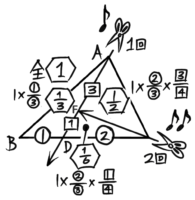
さっき切り分けるとDが頂点になります。その頂点Dから今度はACを3:1に分ける点Eに向かって切り分けます。
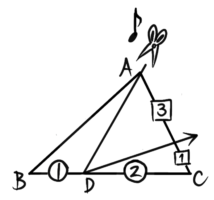
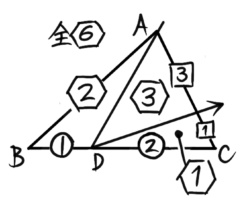
△ADCがさらに3:1に切り分けられて、△ADEと△CDEの面積比は3:1になります。つまり△ADEは△ADCの3/(3+1)=34になり、△CDEは14になります。
△ADCは面積比②だったので、△ADEは②×34=32に、△CDEは②×14=12になります。
分数の比になっていますが、計算を始めるまではこのままでも良いでしょう。(整数に直したい場合は全部を2倍して2:3:1になります。)
2:3:1に分けられている
ト型に2回切る
2回切るには別のやり方もあります。
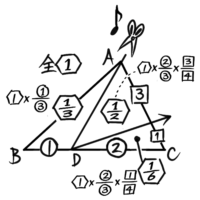
Dまで切ったハサミを1回ひっこめて、次は別の頂点CからADを3:1に分けるFに向かってハサミを入れる「ト」のような切り方です。
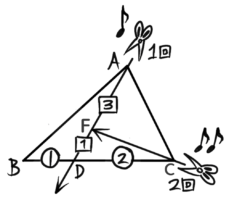
この場合、計算は先程と同じで、△ACFの面積比は32、△DCFは12になります。
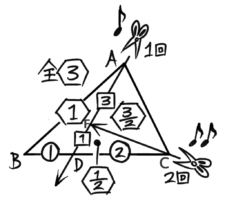
どうせ分数のままにするなら、初めの1:2のときも分数にするのも良いと気づいた人もいるでしょう。全体を1とすると割合が出るので便利なことも多いです。
△ABDは全体の13、△ACFは23にする最初の切断の後2回目の切断で34になるので23×34=12になり、△DCFは23にする最初の切断の後2回目の切断で14になるので23×14=16になります。
さっきの「レ形切り」の方も同じように分数にできます。
このように、2回切って出来る三角形の面積は、分割の割合を2回かけて求めることができます。
3回切る
上のやり方を3回以上行った場合も、同じ様に考えます。
等分割
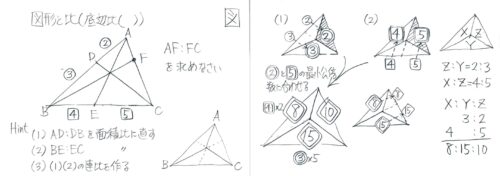
頂点から切って、等しい面積に分けられている三角形の辺の分割の比を求める問題。
三等分
三等分には二通りありますが
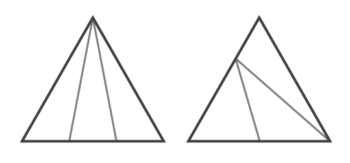
左のパターンは下の辺が1:1:1に分けられるのは明らかなので、問題になるのは右側のパターンです。
まず左端と真ん中の部分に注目すると下の辺は1:1と分かります
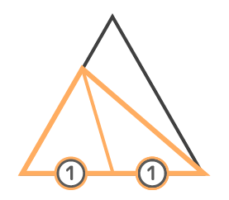
次に左端と真ん中を合わせた形と右端の部分に注目すると、左の辺は2:1と分かります。
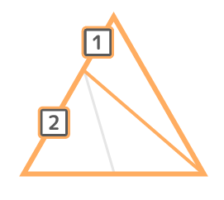
まとめると、こうなります
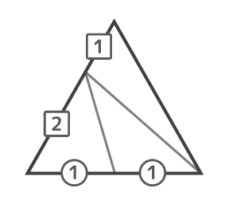
この比を作ることができれば、どの問題にも答えられるでしょう。
四等分
四等分には4つのパターンがありますが
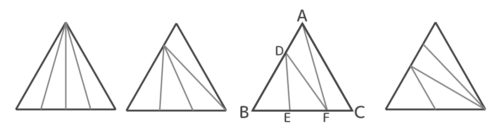
上のパターンに一部分を付け加えたパターンが一番出題されます。
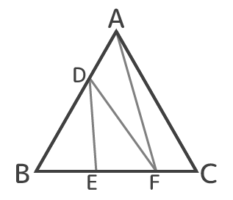
図のBE:EF:FCを求めましょう。
実は、線分FC以外はさっきの三等分のときと同じ分け方なので比も同じです。

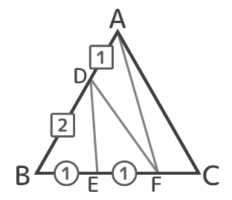
ここで△ABFと△AFCに注目すると、面積が3:1なので、底辺BF:FCも3:1と分かります。
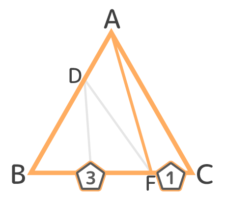
これまでに分かったことを図にすると、こうなっています。
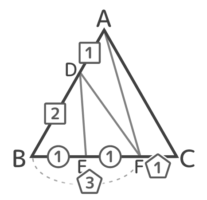
2通りの比で分けられる。
この比をそろえれば終了
BからCまでが「1:1」と「3:1」の二種類の比になっているので、これを一つの比にできれば終了です。
BEとEFはBF(3)を半分にしているのでそれぞれ3/2になります。つまりBE:EF:FC=3/2:3/2:1です。分数ですが、これで比がそろいました。
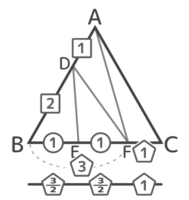
BE:EF:FCが分かった
全部を2倍すればBE:EF:FCは整数の比で3:3:2になりました。
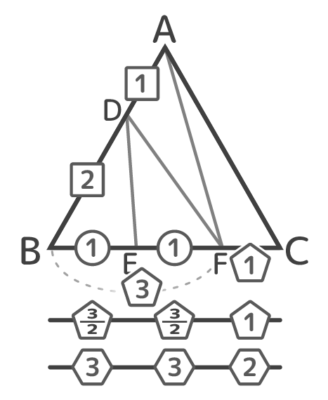
他の4等分パターンの比は単純です。
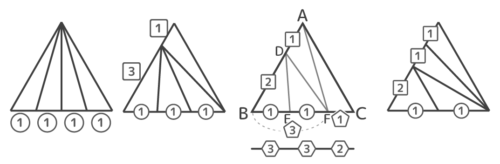
五等分
五等分は8パ ターンあります。一番出題されるのはさっきのパターンの「続き」のパターンです。
BE:EF:FCを求める
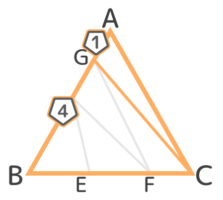
AG:GD:DBとBE:EF:FCを求めましょう
途中までは同じになります。
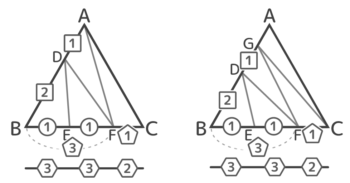
△と△に注目してAG:Gb=1:4を求めます。AB上には「1:1」と「1:4」の二種類の比が混じっています。
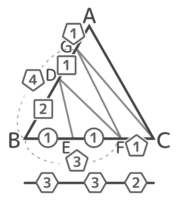
四等分と同じ様に比を揃えます。GB(4)をDは1:2に分けているので、GD=4×1/3=4/3、DB=4×2/3=8/3になります。これらを3倍して整数にすると3:4:8になります。
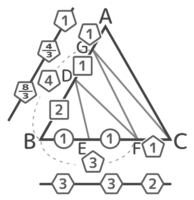
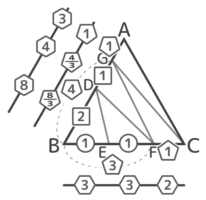
これで、AG:GD:DB=3:4:8、BE:EF:FC=3:3:2と分かりました。
六等分
一番問題になるパターンと解答のみ載せておきます。
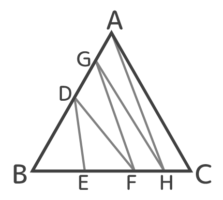
BE:EF:FH:HCを求める
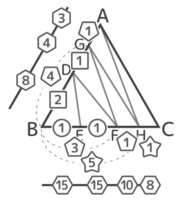
BE:EF:FH:HC=15:15:10:8
等分の問題は以上です。
基本2~辺から辺へ切る
ハサミを頂点ではなく辺に入れて切り分けることもあります。
例えば△ABCの辺ABを1:1に分ける点Dと辺をに分けるEを結ぶように切った場合、△ABC全体を1とすると△ADEはいくつになるかという問題です。
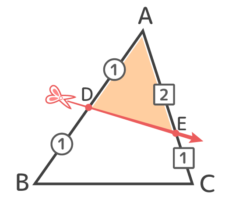
この分け方は実は、さっきの頂点から2回切ったのと同じです。
((図))
したがって△ADEは△ABC全体の12×23=13 になると分かります。
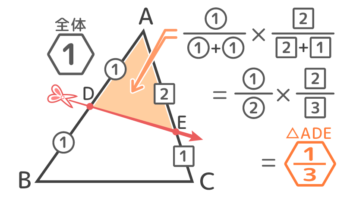
上のような考え方をテストでぱっと使えるように公式にすると次のようになります。
→三角形の二辺をa:bとc:dに分ける点を結んで切り分けると、
先端側の面積は三角形全体のa/(a+b)×c/(c+d)になる。

(例)上の図で△ は△全体の × = になる。
底辺比を使った問題
三辺延長拡大
三角形の三辺を延長した先を結んで出来る大きな三角形が、元の三角形の何倍になるかを考えます。
5:三辺延長拡大
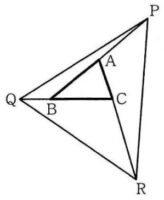
考え方
周りに出来る三角形を分割して考えます
解説
まわりに出来る△PQB,△QRC,△PARがそれぞれ△ABCの何倍かを考えます。
まず、問題文から線分の長さの比を読み取って書き込みます。

はじめに左上の△PQBをQAで2等分してできる三角形の1つ△AQBに注目
(図)
△AQBは△ABCと高さは同じで底辺が1/2になっているので面積は1/2倍。
2等分してできるもう1つの三角形△PQAも同じく1/2になるので、2つを合わせて△PQBは△ABCの1/2倍+1/2倍=1倍と分かる。
同様に考えると△QRCは3倍、△PARも3倍になる。
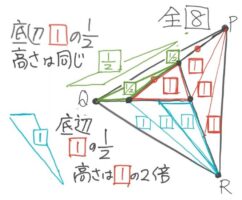
△ABCとの面積比を求める
これらを全部合計すると、新しくできた3つの部分の合計は△ABCの1+3+3=7倍です。
したがって△PQR全体は△ABC自身も合わせて、7+1=8倍になります。
確認テスト
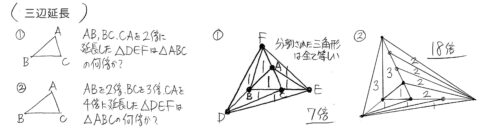
交差切り
この辺りから難しくなってきます。
前提知識
対角線の比=面積比
今までの単純な底辺比にプラス
四角形を対角線で分割した三角形の面積比から、高さにあたる対角線の分割比を求める。
((図))
これを使います。
交差切りの図
例えば、図のような△ABCでDが辺ABを1:1に分けてEはACを2:3に分けている時、DF:FCを求めます。
相似を習った後なら、相似でも解けます。
(図)
優しい問題ではコチラの方が簡単なこともありますが、問題が複雑になるにつれて面積比を使ったほうが易しくなります。
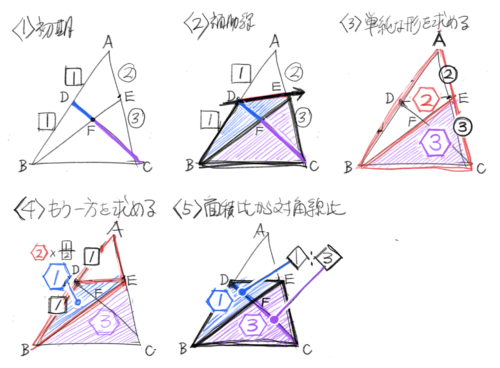
雪印切り(ベンツ切り)
底辺比と面積比の終点がこの「雪印切り」で、これが解ければ入試問題も半分以上が解けるでしょう。(「ベンツ切り」という呼び名が有名)
基本問題
おすすめ教材
 爽茶
爽茶オススメの問題集
●受験算数を総復習したい小6には、コンパクトな「算数ベストチェック」(日能研)や解説が厚い「塾技100 算数」(文英堂)
が良い
●算数や図形が苦手な人には、ほどよい解説もある「算数の基本問題 6年」(日能研)が良い
「分かりやすい!」と評判の
特に塾の授業についていくのに苦労している人は予習に使うのをオススメします。今なら14日間無料♪この期間内に利用を停止すれば料金は一切かかりません。この機会に試してみては?
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。