「点が動く問題が苦手！」という中学受験生の方、
東大卒講師歴20年の図解講師「そうちゃ」が、点が動く問題の解き方・コツを伝えます。
動点問題のコツは、点がどのように動くかをイメージすることです！
記事の真似をすれば動点の問題が苦手ではなくなるでしょう。
速さと旅人算(復習)
爽茶動点の問題は速さの公式を使うので簡単に復習します。
分かるよ！という人はジャンプして下さい
速さの三公式
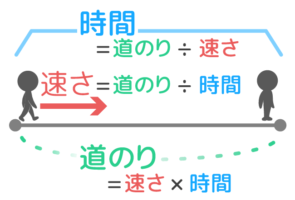
「道のり」「速さ」「時間」の関係
➀：道のり＝速さ×時間
➁：速さ＝道のり÷時間
➂：時間＝道のり÷速さ
旅人算の公式
2つ以上の人・物が移動する場合
出会いと追いつき
❶出会う時間=2人の距離÷速さの和
②2人の距離=速さの和×出会う時間
③速さの和=2人の距離÷出会う時間
❶出会う時間=2人の距離÷速さの差
②2人の距離=速さの差×出会う時間
③速さの差=2人の距離÷出会う時間
円周上の旅人算
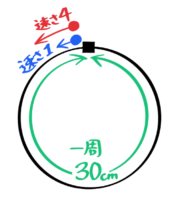
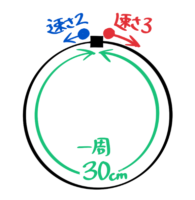
反対方向に出発すると「出会い」(右)
◆最初に追いつく時間(T)=一周÷速さの差
二回目以降に追いつく時間も同じ
→T×1,T×2,T×3(時間)…に追いつきを繰り返す
◆最初に追いつく距離(D)=T×速さ
ニ回目に追いつくまでの距離も同じ
→スタート地点からD×1,D×2,D×3の距離で
追い付きが繰り返される
◆最初に出会う時間(T)=一周÷速さの和
次に出会うまでの時間も同じ
→T×1,T×2,T×3(時間)…に出会いを繰り返す
◆最初に出会う距離(D)=T×速さ
次に出会うまでの距離も同じ
→スタート地点からD×1,D×2,D×3…
の地点で出会う
以上がよく分からない人は関連記事「速さの基本」や「旅人算まとめ」を見て下さい。
動きをイメージ♪
動点問題のコツは、問題を読んだ後ですぐ小問に行かず、頂点に着く時間を計算して書き込むことです。
例えば、縦6cm横8cmの長方形ABCDの辺上をAから出発してB→C→D→Aと2cm/秒の速さで一周する点Pがある場合を考えます
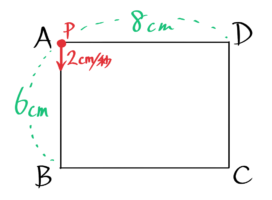
まずタテヨコの辺を移動するのにかかる時間を計算します。AからBまで6÷2=3秒がタテの移動時間、BからCまで8÷2=4秒がヨコの移動時間です。
それを使って、Bに着くのが3秒後、Cに着くのが3+4=7秒後、Dに着くのは7+3=10秒後、Aに戻るのは10+4=14秒と分かるので、それを書き込みます。
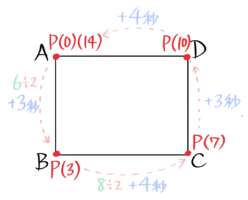
こうしておけば、例えば問題に「12秒後の…」と書いてあれば「点Pが辺AD上にある時で、もうすぐ一周するな」とすぐにイメージできますね。
このように通過時間を書き込むことで、状況をすぐにイメージできるのです。
確認テスト
A=B=C=cmである三角形ABC上を3cm/秒の速さでA→B→Cと移動する点Pがある。点Pが各頂点に着く時刻を書き込め。
ある時刻の点の位置
動点の大まかな動きが分かったら、ある特定の時刻(例：3秒後)での点の位置をパッと求められるようにします。
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。