「速さを予習しておきたい!」という中学受験生の方、その心がけ素晴らしいです。まかせて下さい!
それに対して、最近塾で「速さ」を初めて学習して「思ったより簡単じゃん。楽勝♪楽勝♪」と思っている人は、危ない!
「速さ」は5年6年にかけては受験算数全体でも一番難しくなります。今のうちに「応用につながる基本」を固めておかないと、後で泣きますよ(マジで)
この記事では、東大卒講師歴20年の図解講師「そうちゃ」が入試や応用問題につながる速さの基本を詳しく分かりやすく説明します。
記事を読んで真似すれば、速さが得意になる準備が整って、学年が上がって速さが非常に難しくなっても「楽勝♪楽勝♪」とこなせるかもしれませんよ!
目次をクリックすると好きなところにジャンプできます。

目次(クリックでジャンプ)
速さの基礎
(受験小4)(学校小6)
速さの意味
「速さ」って何でしょうか?
「速さ」とは「単位時間あたりに進む」「道のり」です。
「単位時間」というと難しく聞こえますが、「1秒」「1分」「1時間」など時間の単位に「1」をつけたものです。
例えば「時速」=「1時間で進む」「道のり」という意味です。
だから「時速4km」=「1時間で」「4km」進む速さ になります。
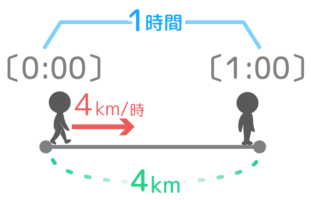
同じように考えると、
分速=「1分間で進む道のり」
秒速=「1秒間で進む道のり」
になります。
→「単位時間あたりに進む距離(道のり)」
・時速=「1時間で進む道のり」
(例)時速50km=1時間で50km進む
・分速=「1分間で~」
(例)分速2m=1分間で2m進む
・秒速=「1秒間で~」
(例)秒速5cm=1秒間で5cm進む
確認問題
次の速さが意味することを答えなさい
(1)時速4km
→1時間に進む道のりが4kmであること
(ちなみに、これは人が歩く速度です)
(2)分速60m
→1分間に進む道のりが60mであること
(ちなみに、これも人が歩く速さです。)
(3)秒速600m
→1秒間に進む道のりが600m!であること
(ちなみに、これは銃の弾丸の速度!です)
速さの公式
「速さの問題」で聞かれるのは「道のり」「時間」「速さ」の3つです。それぞれを求めの方を考えます。
道のりを求める
「時速4km」で歩く人が「3時間」歩いた道のりはどれくらいでしょう?
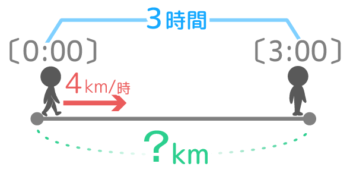
はじめの1時間で4km、次の1時間でさらに4km、最後の1時間でさらに4km…合計すると12kmです。
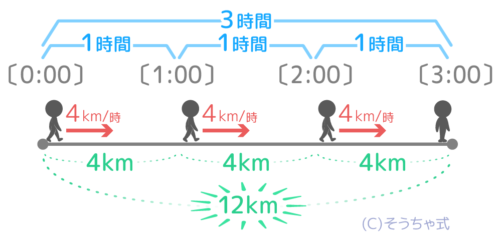
これを一発で出すと「4km/時✕3時間=12km」というかけ算になります。これが「道のり」を出す公式になっています。
道のり=速さ×時間
(例)「時速4km」で「3時間」歩いた道のり
→4km/時 x 3時間=12km
速さを求める
では、10kmを2時間で歩く人の速さは時速何k mでしょうか?
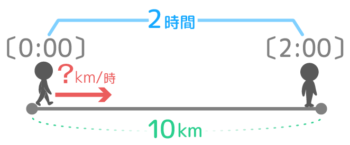
時速は「1時間で進む道のり」なので、2時間で進んだ10kmを2等分すれば良いですね。10÷2=5kmと分かります。
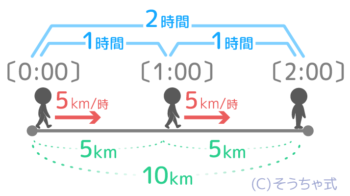
今の式「道のり÷時間」が速さを出す公式になっています。
速さ=道のり÷時間
(例)10kmを2時間で歩く人の速さ
→10km ÷ 2時間=5km/時
時間を求める
12kmを時速3kmで歩くと何時間かかるでしょうか?
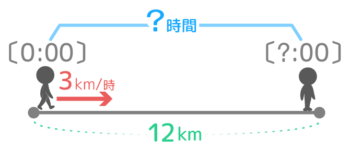
最初の1時間で3km、次の1時間で3km…この合計が12kmになるまで続けるので、12の中に3がいくつあるか、つまり割り算をします。
12÷3=4 で4時間かかると分かります。
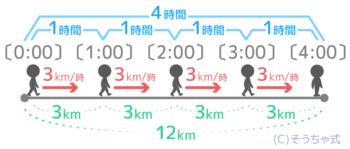
今の式「道のり÷速さ」が時間を求める公式になります。
時間=道のり÷速さ
(例)12kmを時速3kmで歩くと何時間かかるか
12km ÷ 3km/時 =4時間
公式の覚え方
この3つを「速さの三公式」と言います(この名前はどうでも良いですw)
①道のり=速さ×時間
②速さ=道のり÷時間
③時間=道のり÷速さ
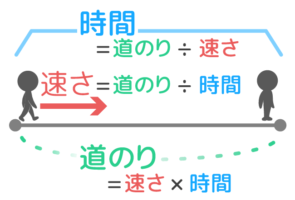
公式を覚える
算数好きの生徒さんなら問題を解いているうちに公式は自然に覚えることもありますが、算数が苦手な生徒さんの場合は(最低限の理解はした上で)公式を反復して記憶してしまう方が良いです。
速さの公式を覚えるのに、カブトムシのような「みはじの図」が有名なのですが(図➀)

もっと良い覚え方があります(「みはじ」という言葉は使います)。
覚えるのは次の三つの事柄ですが、道のりを覚えれば終わりです(太字にしてあります)。
➀速さの問題で出てくる数は「道のり(み)」「速さ(は)」「時間(じ)」の三種類
➁かけ算で出すのは「道のり(み)」
➂わり算は「道のり(み)÷」ではじまる
➀:道のり=速さ×時間
➁:速さ=道のり÷時間
➂:時間=道のり÷速さ
そして、覚える際は一切の迷いなく早口言葉のように早く言えるようにします。さもないと試験では使えませんからね。
そのためには公式に出てくる言葉「道のり」「速さ」「時間」「かける」を「み~」「は~」「じ~」「かけ」と短くすると言いやすいです。こんな感じです。
➀み=は×じ「み~いこーるは~かけじ~」
➁は=み÷じ「は~いこーるみ~わるじ~」
➂じ=み÷は「じ~いこーるみ~わるは~」
これを何度も音読して体に覚えさせましょう。覚えた人は確認テストを。
時速20kmで3時間進むと何km先にいる?
→( 道のりを求めるので、速さ(20)×時間(3)=60km先 )
4時間で48km進む速さは時速何kmか?
→( 速さを求めるので、道のり(48)÷時間(4)=時速12km )
25kmを時速5kmで進むと何時間かかる?
→( 時間を求めるので、道のり(25)÷時間(5)=5時間 )
速さの基礎を詳しく見たい人は姉妹サイト「そうちゃ式 別館(算数/数学)」の「速さの基本」を見て下さい。
 爽茶
爽茶速さと単位

速さの問題は公式を使う前に単位を直したりしないといけないことがあります(難しい理由の一つ)
速さの単位
今まで出てきた単位に比べると、速さの単位は複雑です。なぜなら速さの単位は2つの単位を含んでいるからです。
例えば「時速50km」は時間を表す「時」と長さを表す「km」を含んでいます。
そして、時間と長さの単位の組み合わせで速さの単位はかなり沢山作れます。ざっと挙げると…
「秒速◯mm」「秒速◯cm」「秒速◯m」「秒速◯km」
「分速◯mm」「分速◯cm」「分速◯m」「分速◯km」
「時速◯mm」「時速◯cm」「時速◯m」「時速◯km」
ただ、実際に使われているのは
「秒速◯cm」、「分速◯m」、「時速◯km」
この3つが多いです。
●秒速◯cm
(例)秒速3cm(「3cm/秒」とも)
→点が動く問題で使われる
◆分速◯m
(例)分速60m(「60m/分」とも)
→人が歩く問題で使われる
◆時速◯km
(例)時速4km(「4km/時」とも)
→実生活で人が歩く速度とされる
速さの単位を変更する(準備)
上で書いたように速さは2つの単位を含んでいるので変換が面倒くさいです!
コツは、頭が混乱しないように、まず「時間」「長さ」のどちらか一方だけの変換を行い、それが終わったら残りの変換を行うことです。
単位時間の変更
分速と秒速の関係を考えると…分速は1分間で進む道のり=60秒で進む道のりです。一方、秒速は1秒間で進む道のりなので、分速は秒速の60倍になります。
例えば、秒速2cmを分速に直すと、2cm×60=120cm なので 分速120cmになります(長さの単位をmに直すのはひとまずおいて)。
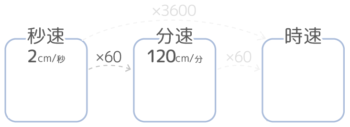
同じように、時速は分速の60倍です。例えば分速50mを時速に直すと、50m×60=時速3000mになります(長さの単位をkmに直すのは後にしましょう)
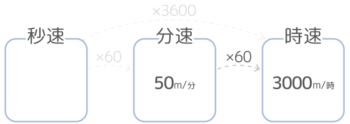
さらに秒速と時速を比べると、時速は秒速の60倍の60倍なので、60×60=3600倍になります。秒速2cmは2cm×3600=時速7200cmになります(長さの単位は後で直しましょう)
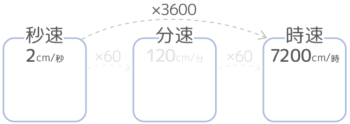
このように、秒速→分速→時速にするたびに60倍されていきます。
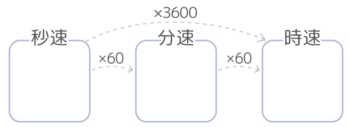
反対に、秒速は分速を60で割った大きさに、分速は時速を60で割った大きさになり、秒速は分速を3600で割った大きさになります。
ただ、60で割ると割り切れない場合が多いので、代わりに×160とするのをすすめます。
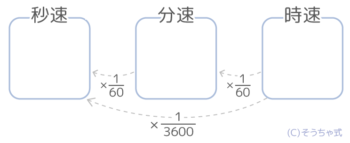
このように単位時間の変更は「横」のイメージです。
◆単位時間を大きくする(→)と速さは60倍
◇単位時間を小さくする(←)と速さは160倍
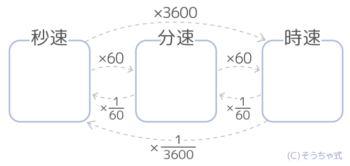
確認テストをどうぞ。ここでは長さの単位は変えないので数が大きくなったり小さくなったりしますが、気にしないで下さい(このすぐ後で分かりやすくなります)
秒速10cm=分速□cm=時速□cm
→( ×60を続けて、秒速10cm=分速600cm=時速36000cm )
分速200m=時速□m
→( ×60して、分速200m=時速12000m )
時速36km=分速□km=秒速□km
→( ×160を続けて、時速36km=分速35km=秒速1100km )
分速12m=秒速□m
→( ×160して、分速12m=秒速15m )
長さの変更(復習)
次は長さの変更です。これは復習になりますが、一応確認します。
●1cm=10mm
●1m=100cm=1000m
●1km=1000m=100000cm
これを使って、速さの「長さ」だけを変換してみます。
例えば、「時速5000m」は5000m=5kmなので「時速5km」になります。また5000m=500000cmなので「時速500000cm」とも言えます((汗))
先程の単位時間の変化を「横」とするならこちらは「縦」の変化としておきましょう。
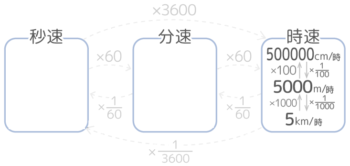
確認テストをどうぞ
時速30000m=時速□km
→( 時速30000m=時速30km )
分速0.05km=分速□m
→( 分速0.05km=分速50m )
秒速0.0003km=秒速□cm
→( 秒速0.0003km=秒速30cm )
速さの単位を変える
いよいよ「単位時間」と「長さ」の両方を変える問題です。
単位時間を大きくする
一段階の変化
例えば「秒速100cmは分速何mか」を考えます。
➊まず秒速を60倍して分速に直します。 秒速100cm→分速6000cmです。
➋次にcmをmに直します。分速6000cm→分速60mです。これで秒速100cmは分速60mと分かりました。
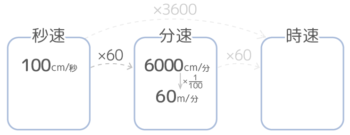
➋次に縦(↓)に1/100する
実際には計算はまとめて1回で終わらせます。
100cm/秒×60×1100=100×60×1100=60m/分
一発約分して計算終了♪
このように、単位時間を大きくする場合はまず単位時間を直してから長さの単位を直すのが簡単です。
図では「横(単位時間)→縦(長さ)」のイメージです。
二段階の変化
今度は秒速80cmは時速何kmか、二段階に変化させます。
まず横(→)に一気に二段階3600倍して80×3600=時速288000cmになります。次に縦(↓)に1/100して2880m/時。更に縦(↓)に1/1000して2.88km/時と分かります。
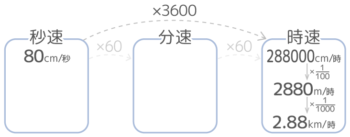
次に縦(↓↓)に1/100、1/1000する
この場合も、実際の計算はまとめて1回で終わらせます。
80cm/秒×3600×1100×11000=80×3600×1×1100×1000
=8×36100=7225km/時
(または)=288100=2.88km/時
気づいたら、100のままにして小数にしても良い
単位時間を小さくする
一段階
時速3.6kmは分速何mか考えます。
ここで時速を分速に直すには3.6を60で割らないといけません(または×160)。ちょっと面倒です。
そこで長さの単位の方を先にkmからmに直します。時速3.6km=時速3600mです。これで割りやすくなりました。
次に時速を60で割って(×160して)分速に直すと分速60mと分かります。
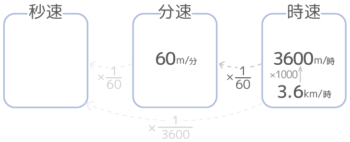
実際には計算はまとめて1回で終わらせます。
3.6km/秒×1000×160=3.6×1000×160=3600×160=60m/分
このように、単位時間を小さくする場合はまず長さを直してから単位時間を直すのが簡単です。
図で見ると「縦(長さ)→横(時間)」です。
ニ段階
最後は時速2.7kmは秒速何cmか出してみましょう。
まず縦(↑↑)に1000倍,100倍して270000cmに直します。これを横(←←)に×13600して2700003600=270036=3004=75cm/秒と分かります。
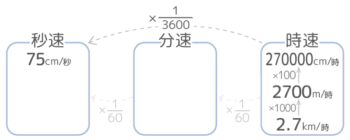
次に横(←←)に×13600
この場合も、実際の計算はまとめて1回で終わらせます。
2.7km/時×1000×100×13600=2.7×1000×1003600
=270036=75cm/分
では、確認テストをやってみましょう。
分速200m=時速□km
→( 分速を60倍して時速に直すと時速12000m )
→( mをkmに直すと時速12km )
秒速50cm=時速□km
→( 秒速を3600倍して時速に直すと時速180000cm )
→( cmをkmに直すと時速1.8km )
分速54m=秒速□cm
→( mをcmに直すと分速5400cm )
→( 分速を÷60して秒速に直すと秒速90cm )
時速1.62km=秒速□cm
→( kmをcmに直すと時速162000cm )
→( 時速を÷3600して秒速に直すと秒速45cm )
時間の単位をそろえる
基礎(復習)
時間の単位について復習します。こうでした。
1分=60秒
1時間=60分=3600秒
そろえ方
速さの問題では、時間は「時間」「分」「秒」のどれかにそろえないと公式が使えません。
たとえば1時間20分そのままでは計算に使えないので、「○時間」か「●分」に直さないといけません。
時間→分(分→秒)
「分」にそろえる場合、1時間=60分なので、1時間20分=60分+20分=80分です。
分→時間(秒→分)
反対に「時間」にそろえる時は、20分を時間に直します。ちょっと悩むかもしれません。
1時間=60分なので20分は2060時間、約分して13時間と考えて、1時間20分=113時間=43時間です(かけ算か割り算をするので仮分数に直しておくと便利です)。
●1分=60秒、1時間=60分を利用する
(例)1時間20分を「分」にそろえる
→60分+20分=80分
●1分=160時間、1秒=160分と考えて分数にする。
(例)1時間20分を「時」にそろえる
→1時間+2060時間=113時間=43時間
いちいち約分するのが面倒くさい場合は、よく出てくる数字と分数の対応を覚えてしまうと良いでしょう。
例えば「12分→15時間」と憶えておけば、36分=12分×3=15時間×3=35時間 とパッと暗算できますね
分→時間分数 と利用例
◆5分→560=112時間
(例)25分=5分x5=512時間
◆6分→660=110時間
(利用例)18分=6分x3=310時間
◆10分→1060=16時間
(利用例)25分=5分x5=512時間
◆12分→1260=15時間
(利用例)36分=12分x3=35時間
◆15分→1560=14時間
(利用例)45分=15分x3=34時間
◆20分→2060=13時間
(利用例)40分=20分x2=23時間
◆30分→3060=12時間
(これは利用例は無し)
理解できた人は、確認テストをどうぞ
X-1:時間の単位変換
解説
1分=160時間なので、35分=3560=712時間です。
ウラ技
慣れてきたら「5分=112時間」と憶えておいて、35分=112x7=712時間、と1秒で出しましょう♪
解説
15分=1560=14時間なので、1時間15分=114時間=54時間です。計算で使うのは仮分数なので、答えに書くまでは仮分数にしておきます。
解説
48分=4860=45時間なので、2時間48分=245時間=145時間です。
解説
1時間=60分なので、23時間=23x60=40分です
ウラ技
少し慣れたら「13時間=20分」と憶えておいて、
23時間=20分x2=40分 と0.5秒で出しましょう♪
解説
小数も分数と同じように計算します。
1時間=60分なので、0.4時間=0.4×60=24分です
解説
2時間=2×60=120分、15時間=15x60=12分なので、215時間=120+12=132分です
別解
215時間=115時間=115x60=132分 計算に自信がある人はコチラでも良いでしょう
分かりましたか?
これで速さの文章問題を解く準備が出来ました♪
速さの文章問題
文章で書かれている問題です。
速さの状況図
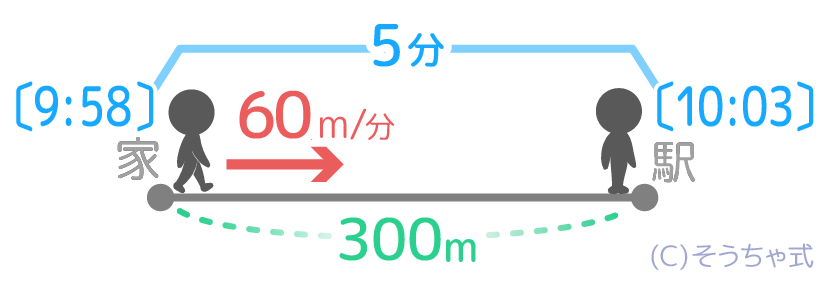
例えば「300m離れた駅に向かって9時58分に家を出発したAさんが駅に10時3分についた時、Aさんの速さを求めなさい」という問題
聞かれているのは「速さ」ですが、いきなり答えを出そうとせずに、まず問題文を図にしてみます。
❶「家」と「駅」を両端に線分を書いて道のり300mを書きます。
❷家を出発する人と時刻「9:58」を書きます。人の速さが書いていないので「?」にしておきます。
❸駅に到着した人と時刻「10:3」を書きます
❹家から駅にかかった時間は5分なのでそれも書きます
これで問題文を全て図にしたので、ここから速さ「?」を考えます。
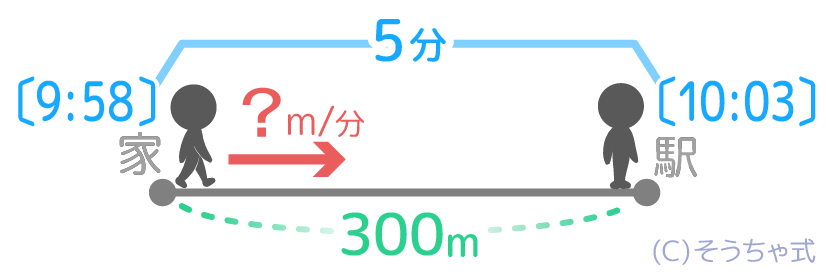
速さの公式「は=み÷じ」を思い出して道のり300mと時間5分を使って、速さ=300m÷5分=60m/分と分かりました。
❺この数字も図に書き込んで終了です。
確認テスト(作成中)
速さが変わる問題
速さが変わる問題では、スタート地点だけでなく速さが変わった場所にも人と速さ(と時刻)を書きます。
例えば「学校の登校時刻は8:20分までです。Aさんは8:10に家を出て、はじめ分速50mで歩いたが途中で時計をみたら登校時刻まで6分しかなかったのでスピードを分速80mに上げて学校まで歩いたら4分前に学校についた。家から学校までは何mあるか?」を考えます。
人を書き足す
さっきと同様に、まず状況図を書きます。
❶家と学校を両端に線分を書きます。道のりは書き込まなくてもOK
❷家を出発する人と時刻・速さを書き込みます
❸スピードをアップした場所をテキトーに決めて、人と速さを書き足します。時刻は8:20の6分前なので8:14と分かります。
❹学校についた人を書きます。時刻は8:20の4分前なので8:16と分かります。
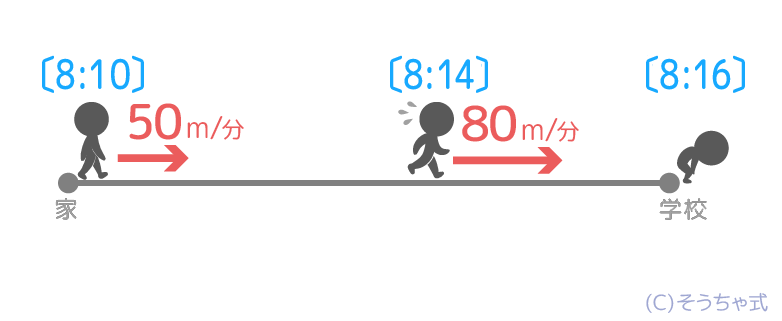
ここから、分かることは何か考えてさらに書き込みます。
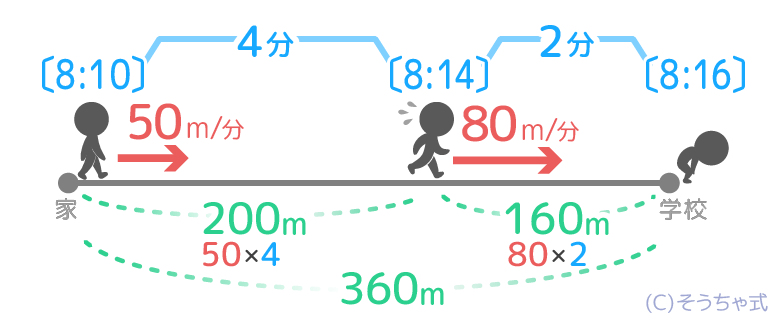
❺図を書くと50m/分で歩いた時間が4分、80m/分で歩いた時間が2分と分かるので書き込みます。
❻50m/分で歩いた道のりが50×4=200m、80m/分で歩いた道のりが80×2=160mと分かるので書き込みます。
❼学校までの道のりが200+160=360mと分かりました。
確認テスト(作成中)
複雑な問題
例えば「Aさんは本屋に本を買いに60m/分の速さで10時に家を出発したが、120m歩いたところで途中で財布を忘れたことに気づき同じ速さで家に戻った。5分で財布を探してから、さっきの1.5倍の速さで再び本屋に向かい 10時13分に本屋についた。家から本屋までは何mか?」
図がゴチャゴチャに…
今までのように状況図を書いてみると
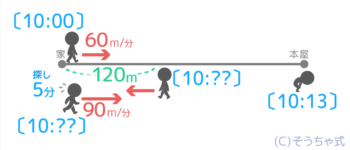
行ったり来たりしているので、図がかなりゴチャゴチャになりました(汗)
もともと、速さの問題は他の分野の問題よりも図を書くのが難しいのです。
難しくなるのは、異なる時間帯の状況を一つの図にまとめているからからです。
時刻ごとに状況図を分ける
そこで、時刻ごとに状況図を分けて書いてみます。
❶スタート(10:00)(速さ60)
❷引き返すところ(120m)
❸家に引き返したところ。
➍5分間の財布探し
➎再スタート(速さ60×1.5=90)
➏図書館に到着(10:13)
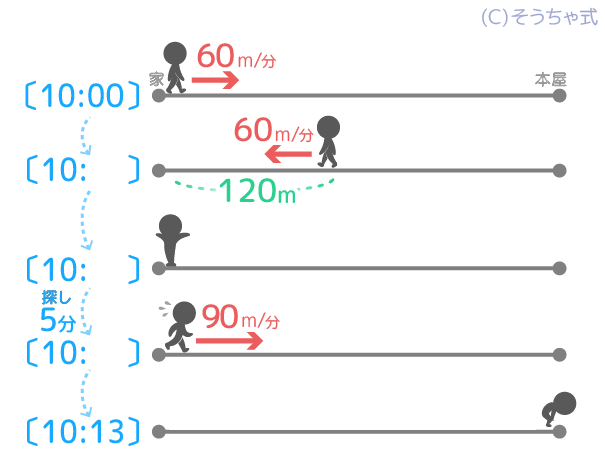
➋引き返すところ(120m)
➌家に引き返したところ
➍5分の財布探し
➎再スタート(速さ60×1.5=90)
➏図書館に到着(10:13)
➐引き返す120m先まで行くのにかかる時間120÷60=「2分」で戻るのにかかる時間も同じ「2分」です。
これで家を再び出発したのが10時9分と分かるので、➑図書館までの時間が4分で、➒道のりは90×4=360mと分かりました。
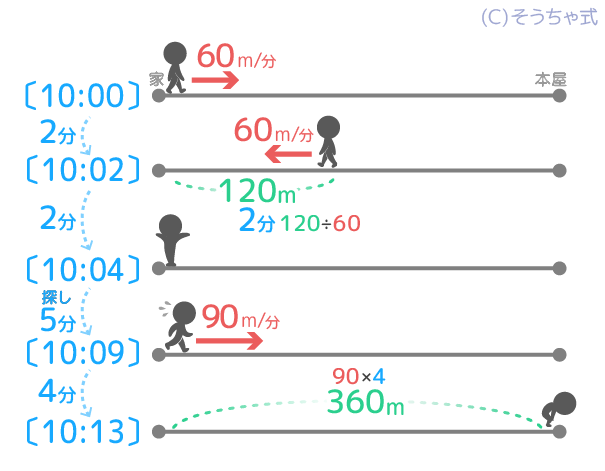
➋引き返すところ(120m)
➌家に引き返したところ
➍5分の財布探し
➎再スタート(速さ60×1.5=90)
➏図書館に到着(10:13)
➐戻るのにかかった時間は2分
➑本屋までは4分
➒本屋までは90×4=360m
分けて書くのが面倒くさいように思えますが、分けることでアレコレ考えずに書くことに集中できますし図も余裕があるので図を見て考えやすくなります。
この後問題が難しくなったとき(人の数が増えたりします)に、これが威力を発揮するので真似してみて下さい。
確認テスト(作成中)
 爽茶
爽茶平均の速さ(受験小5)
「平均の速さ」の意味
最近乗った電車を思い出してください。
止まっていた電車が駅を発車した後スピードが上がっていきます。そのスピードでしばらく走った後、次の駅に近づくとりスピードが下がっていき停車…という風にスピードが変わりますね。
さて、ここで「電車の速さは?」と聞かれたら何と答えればよいでしょうか?最高速度では速すぎるし…意外と答えづらくありませんか?
そこで、電車が走った「道のり」をかかった「時間」で単純に割った速度を「平均の速度」としています。
●平均の速さ
=全部の道のり÷全部でかかった時間
基本の公式と並べてみると、日本語が少し変わっただけで、中身は変わっていないのが分かります。
●速さ
=道のり÷時間
●平均の速さ
=全部の道のり÷全部でかかった時間
問題を解いてみましょう
5-1-1:平均の速さ
解法
「平均の速さ=全部の道のり÷全部でかかった時間」の公式で計算します
解説
全部の道のりは6+10+8=24km全部でかかった時間は11:10-10:30=0:40で40分
求める答えは「時」速なので「分」を「時」に直しておきます。1時間は60分なので、40分=4060=23時間です
以上より、平均の速さ=(全部の道のり)÷(全部でかかった時間)=24÷23=36km/時になります。
往復する場合
同じ道のりを往復した場合が良く問われます。
平均の速さを求める
4-2:往復の平均の速さを求める
(解説)
まず状況図を書きます。ここでは一つにまとめて書きました。
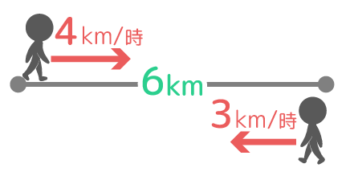
を図に書きこむ
速さの三公式で時間が計算できるので、聞かれていなくてもすぐに計算して書き込みます。
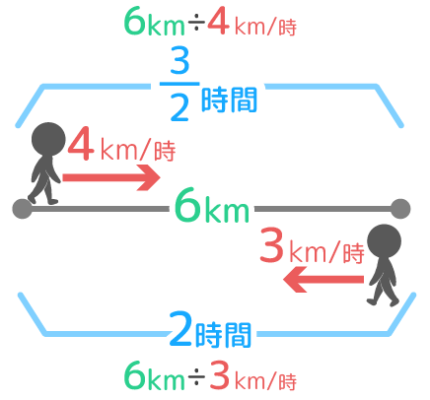
これを見ながら「平均の速さ=全部の道のり÷全部でかかった時間」の式を作ればOKです。
全部の道のりは片道6kmの往復なので、6×2=12km
全部でかかった時間は32+2=72時間です。
したがって、往復の速さは12÷72=247=時速337kmです
km/時
((図))
平均の速さは中途半端な数字になることがあるので最初から分数で計算しましょう。
往復の場合も入れて公式にすると次のようになります。
●平均の速さ
=全部の道のり÷全部でかかった時間
●往復の平均の速さ
=(片道×2)÷(往復にかかった時間)
途中の速さを出す
4-3:途中の速さを求める
このときの平均の速さが9km/時だったとすると自転車の速度は時速何kmだったか?
解説
まず問題文の数値だけを使った状況図を書きます。
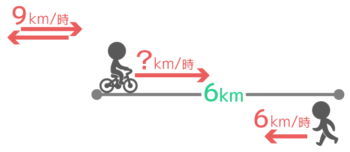
速さの公式で帰りにかかった時間が1時間と分かります。
また往復の速さの公式を変形した「往復にかかった時間=往復の道のり÷平均の速さ」を使うと、往復にかかった時間が12÷9=43時間と分かります。
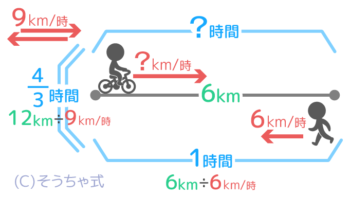
これで行きにかかった時間は43-1=13時間と分かります。
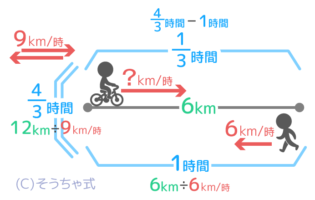
自転車は6kmを13時間で走ったので、自転車の速さ=6÷13=18km/時と分かりました
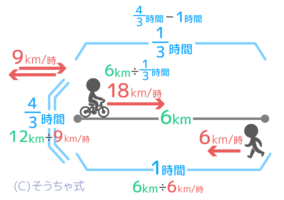
小まとめ
平均の速さの公式をまとめるとこうなります
●平均の速さ
=全部の道のり÷全部でかかった時間
→平均の速さ=24km÷4060時間=36km/時
●往復の平均の速さ
=(片道×2)÷(往復にかかった時間)
行きは時速4km、帰りは時速3kmで往復
→行きにかかる時間は6/4=3/2時間
→帰りにかかる時間は6/3=2時間
→平均の速さ=(6×2)÷(32+2)=337km/時
もっと問題を解きたい人のために、記事下にオススメ教材を紹介しています。
ダイヤグラム(受験小5)
状況図以外にも、便利な図があります。それが「ダイヤグラム」です。
ダイヤグラムの意味
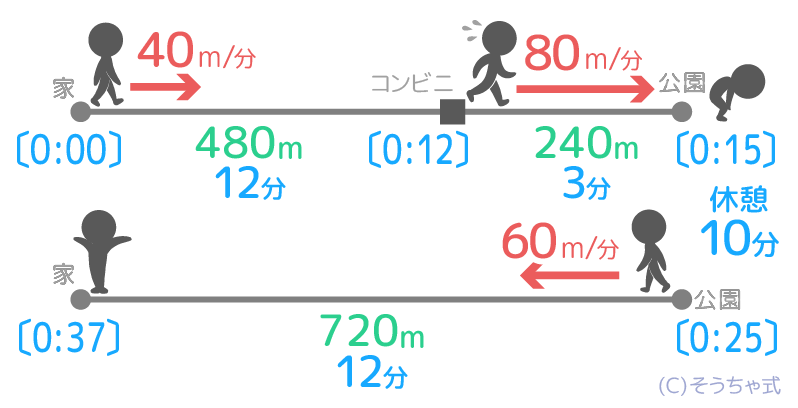
A君は家から720m離れた公園に散歩に出かけました。はじめは40m/分で歩き、480m先のコンビニの前で80m/分に速度を上げて公園まで歩きました。公園で10分休んだ後、60m/分で家に戻りました。
これを状況図にして、時間は計算して書き込んでしまいます。
図1:状況図
家から720m先の公園に、はじめは40m/分で
480m先のコンビニの前から80m/分で歩く。
公園で10分休んだ後、60m/分で家に戻った。
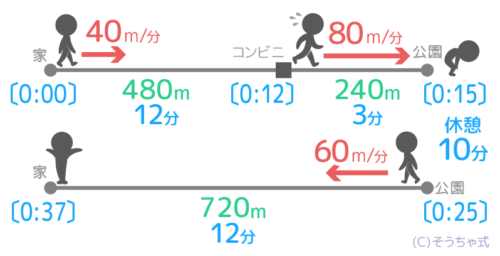
全部で12(行き1)+3(行き2)+10(休憩)+12(帰り)=37分かかったと分かります。
このA君の散歩を「ダイヤグラム」にするとこうなります
図2:ダイヤグラム
家から720m先の公園に、はじめは40m/分で、480m先のコンビニの前から80m/分で歩く。公園で10分休んだ後、60m/分で家に戻った。
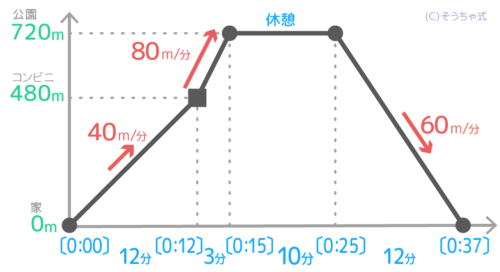
状況図と比べると大体の意味は分かるのではないでしょうか?
縦軸の数字(①)は出発点からを、横軸の数字(②)は出発時からの時刻を示します。
ここではダイヤグラムは山のようになっています。右上りの部分(➂)は、出発点からゴール(折り返し点)まで進んだことを表します。反対に④右下りの部分は出発点に戻ることを表します。
ダイヤグラムの傾きが急な部分(⑥)は速く移動していることを表します。傾きがゆるい部分(⑦)はゆっくり移動していることを表します。平らな部分(⑧)は止まっている(休んでいる)ことを表します。
速さの三公式(道のり、速さ、時間)のうち、「速さ」は直接書いてありません。グラフから自分で計算しないといけません。
例えば、家からコンビニまでの速さを求めるにはグラフ上で家からコンビニまでの距離と時間を240m、12分と読み取って、240m÷12分=20m/分と計算します。
以上がダイヤグラムの意味と読み方です。
→行動をグラフにしたもの
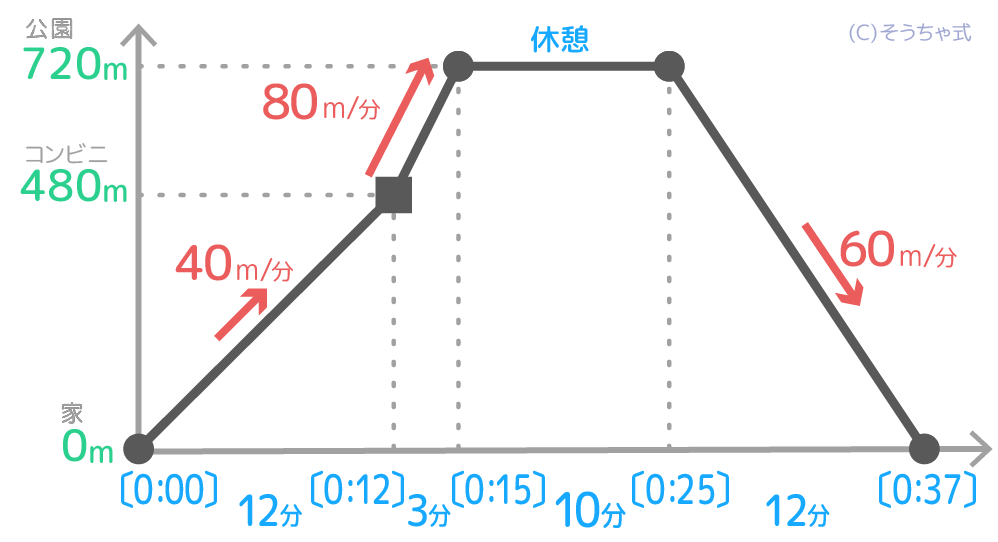
●グラフの縦軸は道のり、横軸は時間を表す
●右上がりは出発地から遠ざかる動きを、
右下がりは出発地に戻る動きを表す。
●急な坂は速度が大きいことを、
ゆるい坂は速度が小さいことを表す。
平らな部分は止まっていることを表す
◆速さはグラフ上に表れないので、
2点の時間差・距離差を使って計算で求める
練習問題で定着
 爽茶
爽茶速さのつるかめ算(受験小5)
つるかめ算は「面積図を使った方法」と「使わない方法(置き換え法)」がありますが、ここでは「面積図を使った方法」で解きます。(小数や分数が答えになる分野では面積図を使います。)
速さの面積図
ここまでに速さの状況図、ダイヤグラムを練習しましたが、速さは面積図にすることもできます。
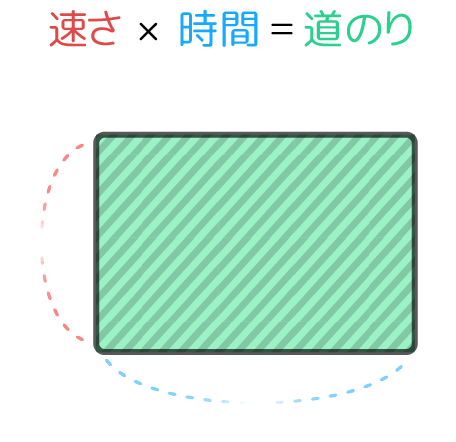
「道のり=速さ×時間」は「長方形の面積=たての長さ×よこの長さ」と同じ関係なので、同じような面積図になります。
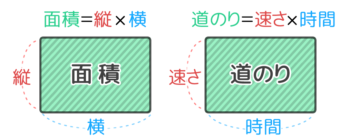
例えば、時速4kmで3時間歩くと12kmを進みました

これを面積図にすると、こうなります。
途中で速さが変わる場合
状況図の説明をした時に速さが変わる問題(例題2)がありました。
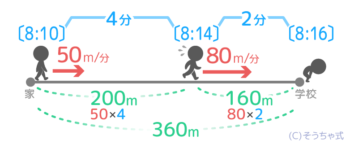
例題2をもう一度見てみましょう。全6分間で360mを進みましたが、➊はじめの4分は50m/分で➋残り2分は80m/分で進みました。

ここでは、全部の道のり360mは50×4=200mと80×2=160mの和です。
すると「(50×4)+(80×2)=160」が作れます。これはL字形の面積図が表す関係と同じです。

つまり、速さを変えた場合の面積図は「L字型の面積図」になるのですね。
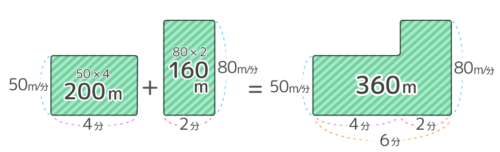
こういうわけで、速さが変わる場合はつるかめ算と同じような問題を作れるのです。
解き方を理解
例えば「家から780m離れた駅まで、はじめは120m/分で走ったが途中で疲れて速度を50m/分にしたら、駅まで10分かかった。歩いたのは何分か?」という問題を考えます。
L字型の面積図はこうなります。面積は道のり780で左の高さがはじめの速さ120、右の高さがあとの速さ50、歩いた時間?を求めます。
図2:速さが変わる問題の例
家から780m離れた駅まで、はじめは120m/分で走ったが、途中で速度を50m/分にしたら、駅まで10分かかった。歩いたのは何分か?
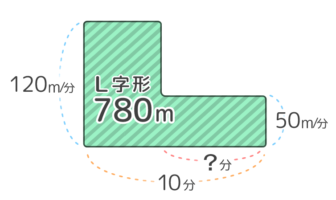
➌全部の道のり780 ➍歩いた時間?
まず➊L字形を包む大きな長方形を作ります。面積は(4+6)×120=1200です。次に➋大きな長方形とL字形の間に「欠け形」を作ります。欠け形の面積は1200-780=420です。
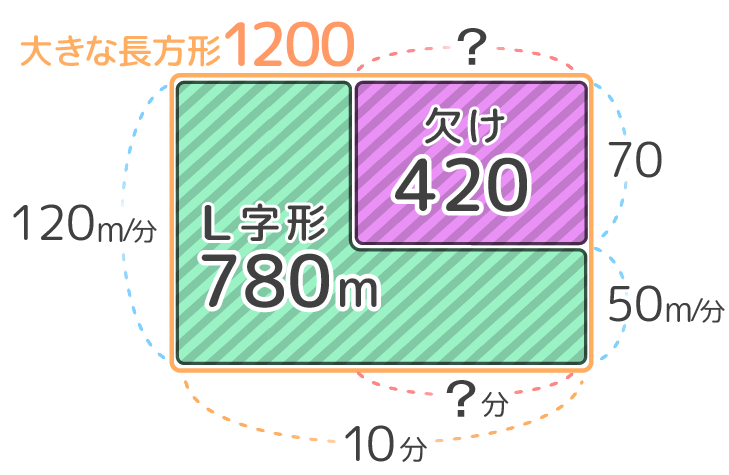
➋欠け形(大きな長方形1200-L字形360=420)
➌欠け形のたての長さは120-50=70なので、欠け形のよこの長さ(?と等しい)は420÷70=6です。

これで走っていたのは6分と分かります。
もっと問題を解きたい人は参考記事「速さのつるかめ算」を見て下さい。
おすすめ教材
 爽茶
爽茶●速さだけを解きたい人には「速さ・旅人算」(サイパーシリーズ)
●受験算数を総復習したい小6には、コンパクトな「算数ベストチェック」(日能研)や解説が厚い「塾技100 算数」(文英堂)
が良い
●予習したい小3小4には、ほどよい解説もある「算数の基本問題5年(日能研)」が良い
分かりやすい!と評判のスタディサプリには有名講師「繁田和貴」氏による速さの授業動画もありますよ。今なら14日間無料。興味がある人は「先取りや予習・復習に! スタディサプリ そうちゃ式のオススメ利用法」へ
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
