旅人算が難しい」という中学受験生の方、「どこから勉強していいか分からない」と途方にくれていませんか?
確かに「旅人算」は難しいのですが、基本から順番に確実に身に着けていけば基本問題は必ず解けるようになります。
そこで難しい問題に取り組んでいる立派なあなたを助けるために、東大卒講師歴20年の図解講師「そうちゃ」が速さの基本から順番に「旅人算」を分かりやすく説明します!
読んだ後は「旅人算」が前より得意になっているでしょう♪
目次(クリックでジャンプ)
速さの基本(復習)
旅人算で出てくる公式は、以前学習した「速さの三公式」と全体の形は変わりません。
そこで、旅人算を学ぶ前に「速さの三公式」をしっかり思い出してください。
①道のり=速さ×時間
②速さ=道のり÷時間
③時間=道のり÷速さ
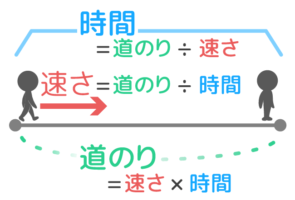
覚え方のコツは「『道のり』だけがかけ算」「残りは『道のり÷』」というように「道のり」だけを覚えることです。
確認テストをどうぞ
時速4kmで3時間進んだ距離は?→( 4×3=12km )
3kmを36分で進む速さは時速何km?→(36分=3660時間=35時間。 )
→( 3÷35=3×53=5より時速5km。)
5kmの道を時速4kmで進むと何時間何分かかる?
→( 5km÷4km/時=54時間=114時間 )
→( 14時間=60分×14=15分なので、114時間は1時間15分。)
これが出来なかった人は「速さの基本まとめ」を見るとよいかもしれません。
旅人算の基本
(直線上の旅人算)
旅人算は離れている2人(以上)の人間が「出会ったり」「追いついたり」する問題です。
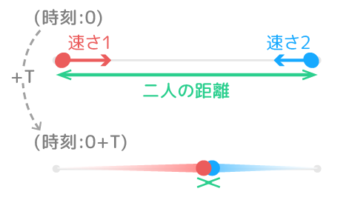
反対方向になっている。
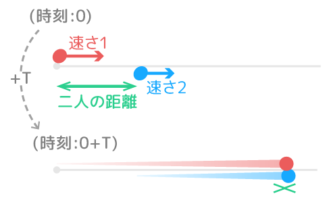
同じ方向になっている。
2つの速さ。出会いはプラス、追いつきはマイナス
旅人算は2人が動くので、速さも2つ出てきます。この2つの速さをどう扱うのかが最初のポイントです。
「出会い」では2つの速さを足し(和)、「追いつき」では2つの速さを引き(差)ます。
●出会い
→2つの速さを足す(和)
●追いつき
→2つの速さを引く(差)
「速さの三公式」のうち「速さ」の部分を「速さの和」と「速さの差」に変えると「旅人算」の公式になります。
「時間=道のり÷速さ」の公式を例に取ると、追いつく場合は「速さ」を「速さの差」に、出会う場合は「速さ」を「速さの和」に変えて、次のようになります。
◆「追いつく」場合
→時間=道のり÷2つの速さの差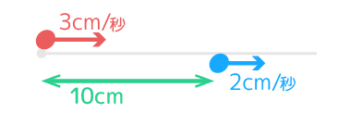 赤が青に追いつく時間は10÷(3–2)=10秒になる
赤が青に追いつく時間は10÷(3–2)=10秒になる
◆「出会う」場合
→時間=道のり÷2つの速さの和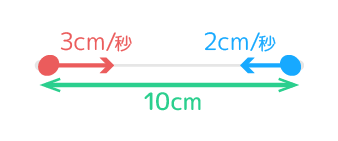 赤と青が出会う時間は10÷(3+2)=2秒になる
赤と青が出会う時間は10÷(3+2)=2秒になる
「追いつき」と「出会い」この2つの場合を順に見ていきます。
「追いつき」の旅人算
移動する人や物の速度(矢印)が同じ方向を向いている場合です。
実は「追いつく」と「引き離す」2つのパターンがありますが…

2人の距離が近づいていく
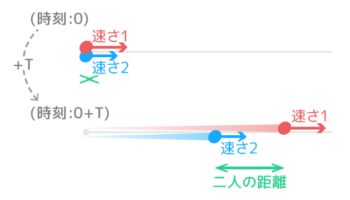
2人の距離が離れていく
どちらのパターンも公式は同じなので、まず「追いつく」パターンをマスターしましょう。
追いつくのにかかる時間
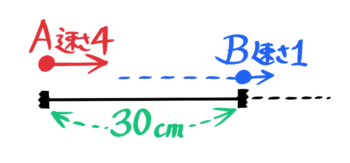
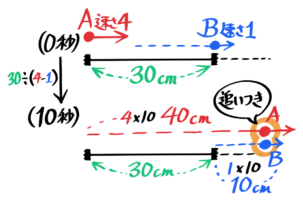
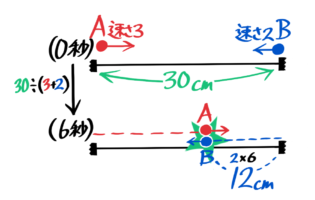
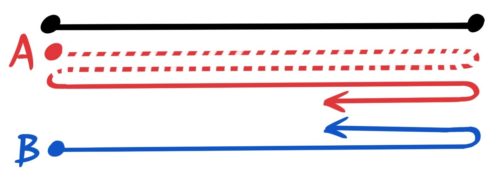
例えば、1cm/秒の速さで進む点Bを、6cm後ろから点Aが4cm/秒の速さで追いかける場合です。
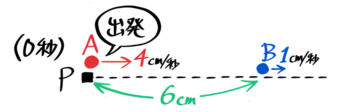
Aが4cm/秒で追いかける
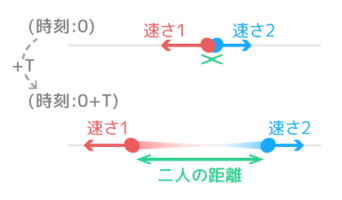
離れている二人の進行方向が同じ場合、速さはマイナス(差)されます。
車や電車に乗っている時に別の車や電車と並んで走ると相手がゆっくり動いているように見えるのと同じ理屈です。
この問題では二点ABは4-1=3cm/秒の速さで近づき、6cm÷3cm/秒=2秒でAがBに追いつきます。
追いつくのは8cm進んだ地点
追いつく時間の公式
基本公式の「速さ」を「速さの差」に変えると追い付きの旅人算の公式になります。
❶時間=道のり÷速さ
②道のり=速さ×時間
③速さ=道のり÷時間
❶追いつく時間=2人の距離÷速さの差
②2人の距離=速さの差×追いつく時間
③速さの差=2人の距離÷追いつく時間
旅人算の公式では、それぞれの「速さ」ではなく、「速さの差」しか出ないことに注意してください。
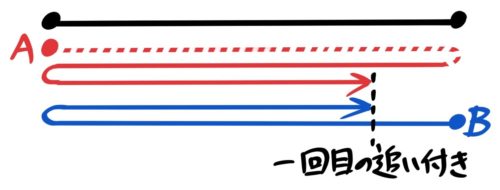
60m/分で歩くBを120m後ろからAが90m/分で追いかけると何分後に追いつくか?
→( 120÷(90-60)=4分後 )
追いつきのダイヤグラム
ダイヤグラム(復習)
動く人や物の行動の様子をグラフにしたものがダイヤグラムでした。
→行動をグラフにしたもの
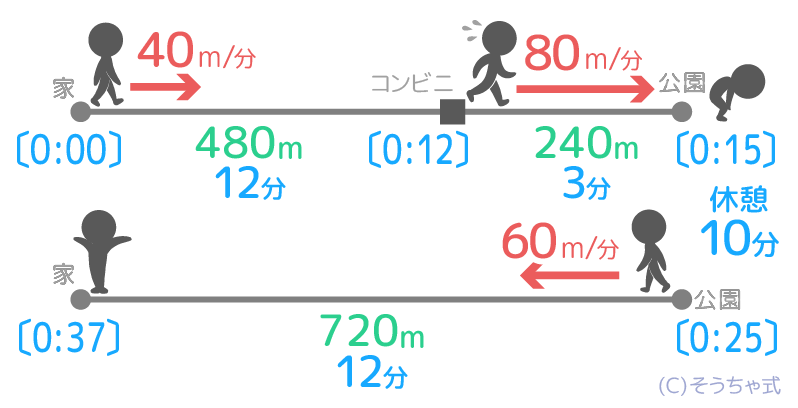
ダイヤグラムを復習したい人は「速さの基礎」内の「ダイヤグラム」を見るとよいかもしれません。
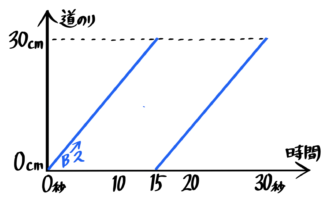
追い付きのダイヤグラム
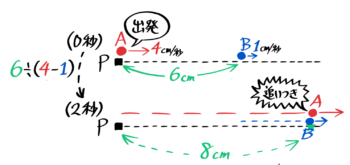
上で見た「1cm/秒の速さで進む点Bを、6cm後ろから点Aが4cm/秒の速さで追いかけたところ、6÷(4-1)=2秒で追いついた」をダイヤグラムにすると、下のようになります。
4cm/秒の点Aが追いかける場合
状況図とダイヤグラム


6cm先を進むBは縦軸の途中から右上がりに伸びる線になり、Aのグラフと2秒後に交わります。
追いつかれる人の全行動
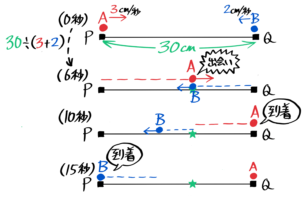
上の例ではいきなりAとBが6cm離れていましたが、テストでは「AとBは同じ地点から、AがBより何秒か遅れて出発する」という問題が多いのです。
そこで、Bが出発してから追いつかれるまでの全部の行動を考えます。
1cm/秒のBが6cm先まで進むのには6秒かかるので、AはBが出発した6秒後に出発したことになります。
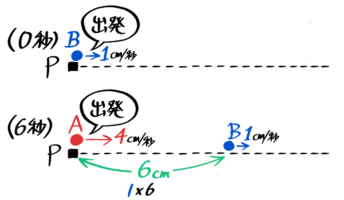
Aは6秒遅れて追いかける
その後はやはり2秒で追いつくので、Bの出発から計測すると8秒後に追いつかれたことになります。
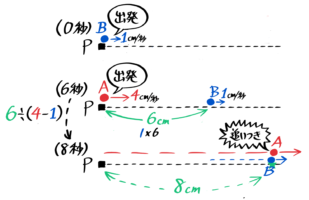
+2秒した8秒後に追いつく
これをダイヤグラムにすると、次のようになります。
状況図(上)とダイヤグラム(下)

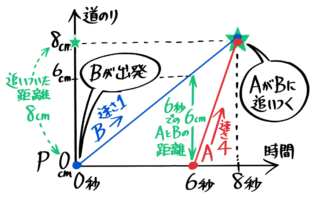
追いかけ始めた6秒でのグラフの垂直の距離6cmが「追いつく時間」の公式で使う「2人の距離」になっています。
60m/分で歩く弟が家を出た3分後に兄が90m/分で追いかけると追いつくのは弟が家を出てから何分後か?
→( 兄が家を出る3分後までに弟は60×3=180m進んでいる )
→( 兄が追いつくのにかかる時間は180÷(90-60)=6分 )
→( 追いつくのは弟が家を出てから2+6=8分後 )
引き離す
(追いついた後などで)同じところにいる速い方が遅い方を引き離す(差をつける)場合にも同じ式を使います。
例えば、速さ3cm/秒の点Aと速さ2cm/秒の点Bが、同じ方向に向かって同時に出発する場合です(50m競争のイメージ)

2つの点の距離が7cmになるのは何秒後か考えると、1秒につき3-2=1cmずつ引き離されていくので7÷1=7秒後とわかります。
公式にすると、日本語が少し変わっていますが「追いつく」場合と中身は同じです。
❶引き離す時間=2人の距離÷速さの差
②2人の距離=速さの差×引き離す時間
③速さの差=2人の距離÷引き離す時間
この「引き離し」の公式は、後で何回も出てくるので必ず覚えておきましょう♪
確認テストをどうぞ
速さ60m/分のAさんと速さ90m/分のBさんが同時に駅に向かって家を出た。先に駅についたBさんがAさんに電話をするとBさんは駅の手前ちょうど120mのコンビニ前を通過した所だった。家から駅まで何mか?
→( AがBに120m引き離されるのにかかる時間は120÷(90-60)=4分 )
→( 家から駅=Bが歩いた距離は90×4=360m )
小まとめ
2人の速さはマイナス(差)される
●追いつく時間=距離÷速さの差
(例)1cm/秒の点Bが出発して6秒後に(6cm後ろから)
4cm/秒の点Aが追いかける
→追いつく時間は6÷(4-1)=2秒後
●追いつきのダイヤグラムは「∧」型に交わる
●引き離す時間=距離÷速さの差
「追いつき」の旅人算は以上です。次は「出会い」の「旅人算です。
「出会い」の旅人算
移動する人や物の速度(矢印)が反対方向を向いている場合です。
実は「出会う」と「分かれる」の2つのパターンがあります(ドラマみたいだw)
この2つは使う公式が同じなので、まずは「出会う」場合を理解しましょう。
出会うまでの時間
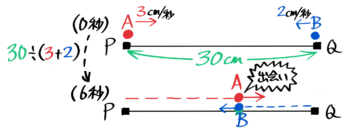
例えば、30cmはなれた点Aと点Bが、それぞれ3cm/秒と2cm/秒の速さで近づく場合を考えます。
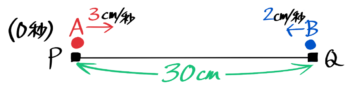
二人の進行方向(速さの矢印の向き)が逆の場合、二人の速さはプラス(和)される。
電車や車に乗っていて別の電車や車とすれ違う時は、すごい速さを感じますね。あれは自分の速さと相手の速さがプラスされるからです。
この問題では二点ABは3+2=5の速さで近づき、30cm÷5cm/秒=6秒で出会います。
出会う時間の公式
「速さの三公式」の「速さ」を「速さの和」に変えると旅人算の公式になります。
❶時間=道のり÷速さ
②道のり=速さ×時間
③速さ=道のり÷時間
❶出会う時間
=2人の距離÷速さの和
②2人の距離
=速さの和×出会う時間
③速さの和
=2人の距離÷出会う時間
追いつきの時と同様、「速さ」ではなく、2つの速さの「和」しか出ないことに注意してください。
確認テストをどうぞ
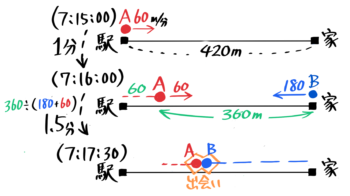
夜7時15分に、A子は420m離れた家に向かって駅から60m/分で歩き始めたが、暗くて怖いので1分後に家に電話して迎えに来るよう頼んで歩き続けた。兄Bがすぐに家を出て180m/分で向かうと二人は何時何分何秒に出会うか
→( 1分後の二人の距離は420-(60×1)=360m )
→( AB2人が出会うのにかかる時間は360÷(60+180)=1.5分=1分30秒 )
→( 2人が出会う時刻は7:15:00+0:01:00+0:01:30=7時17分30秒 )
図
出会いなのに「速さの差」を使うパターン
「出会い」の問題でも「速さの差」を使うパターンがあります。
例えば、距離が分からないRSの両端から速さ5cm/秒のCと速さが分からないDが同時に出発してから4秒後にRSのちょうど真ん中から6cm先で出会った時のDの速さとRSの距離を考えます。
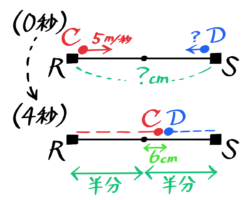
Cが進んだ距離は「半分+6」でDが進んだ距離は「半分-6」なので、CDが進んだ距離の差は(半分+6)-(半分-6)になります。
この計算は小学生にはできないので、線分図的に考えると…
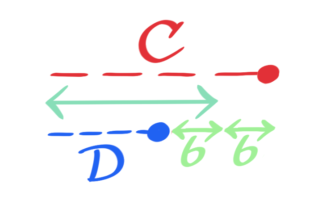
図にすると、差は12と分かる
二人が進んだ距離の差は6×2=12cmと分かります(Cの方がDより長い)。
「引き離し」の公式「引き離される時間=2人の距離÷速さの差」を使うと、4=12÷速さの差 より 速さの差=3なので、Dの速さは5ー3=2cm/秒と分かります。
さらに、速さ5cm/秒と2cm/秒の2人が4秒後に出会ったのでRSの距離=(5+2)×4=28cmと分かります。
出会いの地点とちょうど真ん中がN離れている場合
→2人の進んだ距離の差はN×2なので
AはBをN×2だけ「引き離した」ことになる。
→「出会った(引き離した)時間=2人の距離÷速さの差」
を使って速さの差を求めることができる。
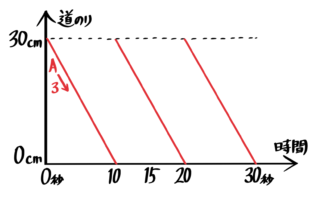
出会いのダイヤグラム
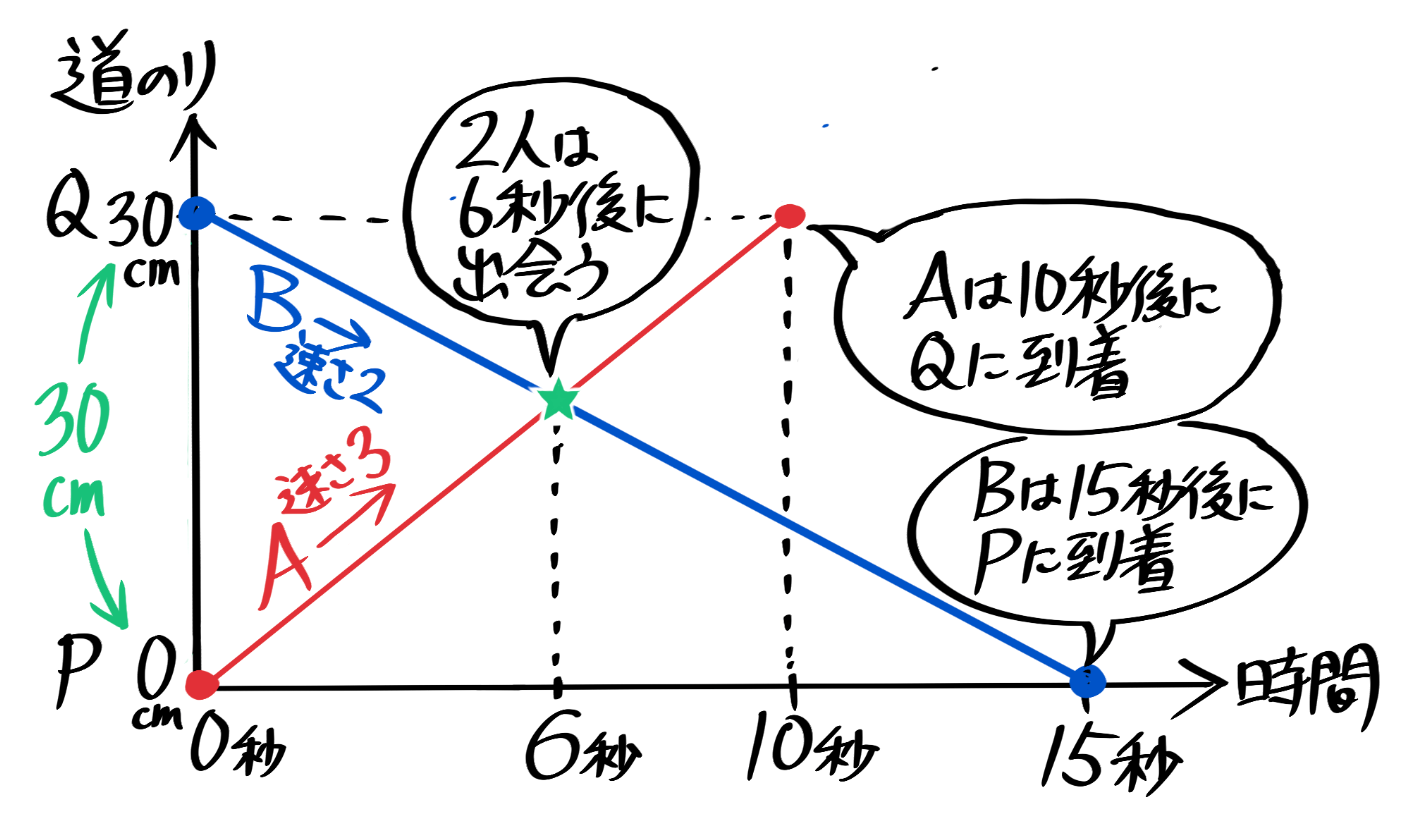
さっきの例、30cmはなれた点Aと点Bが、それぞれ3cm/秒と2cm/秒の速さで近づく場合をもう一度使います。
二点は30cm÷5cm/秒=6秒で出会いました。そこまでをダイヤグラムにすると、こうなります。
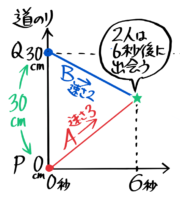
右下がりのBのグラフが
6秒後に交わる(出会う)
Pを出発地Qを目的地にしているので、PからQに向かうAのグラフは右上がりに、QからPに向かうBのグラフは右下がりになります。
AとBがさらに進んで、それぞれQ、Pに着くまでを考えてみましょう。
Aは出発から30÷3=10秒後にQに到着し、Bは30÷2=15秒でPに到着します。
Bは15秒後にPに到着
この全行程をダイヤグラムにすると、こうなります。

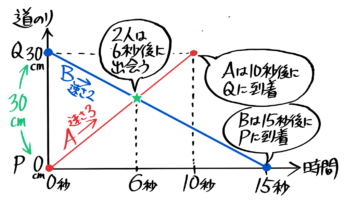
このように、出会いのダイヤグラムは「X」型になります。
旅人算(出会い)のダイヤグラムは「>」で交わる


「別れ」の旅人算
近づいてきた二人がすれ違って別方向に離れていく場合で、「出会い」と同じ公式を使います。
別れにかかる時間
例えば点Aと点Bが反対方向に向かってAは3cm/秒、Bは2cm/秒で同時に動き出す場合です。
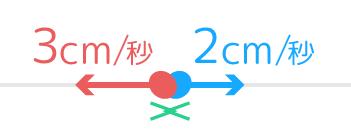
2つの点は3+2=5cm/秒の速さで離れていくので、2点の距離が10cmになるのにかかる時間は10÷5=2秒後になります。
別れの時間の公式
公式にすると、日本語が少し変わっていますが「出会う」場合と中身は同じです。算数が得意な人は覚えなくてもOKです。
❶時間=2人の距離÷速さの和
②2人の距離=速さの和×時間
③速さの和=2人の距離÷時間
別れのダイヤグラム
確認テスト(2021.1作成中)
小まとめ
2人の速さはプラス(和)される
●出会う時間=距離÷速さの和
(例)30cmはなれた2地点PQから、
3cm/秒の点Aと2cm/秒の点Bが同時に出発
→出会う時間は30÷(3+2)=6秒後
●出会いのダイヤグラムは「>」型に交わる
●出会った後は「離れる」
⦿出会い場所と真ん中との距離(N)だけ分かる場合
→2人の進んだ距離の差がN×2なので
「出会った(引き離した)時間=2人の距離÷速さの差」で
速さの差を求める
(例)5cm/秒のCと速さの分からないDが
道のりの真ん中よりも6cm離れた地点で出会った。
→2人が4秒で進んだ道のりの差=6×2=12cm
→速さの差=12÷4=3なのでDの速さ=5-3=2cm/秒

円周上の旅人算
池の周りの道のような円周状の道を2人がジョギングするような場合が円周上の旅人算です。
2人が同じ方向にスタートすると速い方が遅い方を一周分追いかける「追いつき」に、2人が反対方向にスタートすると一周分の「出会い」になります。
反対方向に出発すると「出会い」(右)
それぞれ順番に見ていきます。
円周上の追いつき
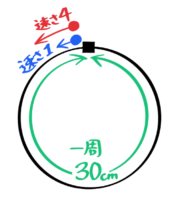
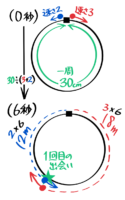
例えば、速さ4cm/秒の点Aと速さ1cm/秒の点Bが一周30cmの円周上の同じ場所から同じ向きに同時に出発する場合を考えます。

1回目の追いつき
追いつく時間を求める~直線にする
1回目の出会いは円を開いて直線に直して考えます。
一周の距離=二人の距離になり「追いつきの旅人算」と同じ図になります。

「直線上の旅人算」の公式を使って、追いつく時間は30÷(4-1)=10秒後と分かります。
追いつく場所を求める
ABどちらかが進んだ道のりを「速さ×時間」で計算します。遅い方で計算するほうが簡単です。
さっき直線に開いた円を元に戻して、おそいBが進んだ道のりを計算します。
1cm/秒×10秒=10cmで、スタート地点から反時計回りに10cmの地点と分かります。
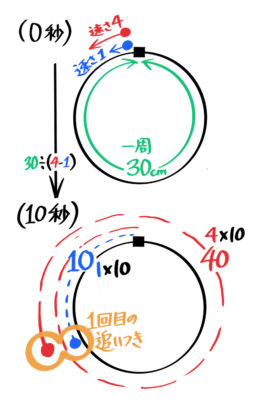
10cm進んだ地点と分かる
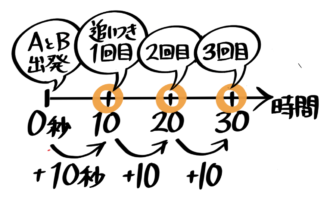
二回目以降の追いつき→周期で考える
追いつき時間の周期
出会いと同じく、追いつきの場合も二回目以降は一回目の時間と同じ周期で追いつきが発生します。
上の例では最初に10秒後においつくので10秒周期になります。
つまり10秒,20秒,30秒…ごとに追いつき(Bから見ると「追いつかれ」)が発生します。
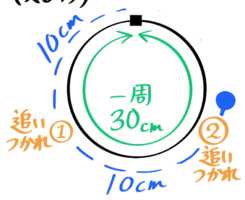
追いつき地点の移り変わり
出会う場合と同じように、遅い方の人に注目して行きます。
Bは10cm進んだ地点で1回目に追い越されたので、2回目は1回目の場所から10cm進んだ地点です。
この後も10cm進むごとに追い越されるのを繰り返します。
追いつきの回数で指定された場合
「Bが5回目に追い越されるのはどの地点でか」のように追いつきの回数で指定された場合は遅い方の移動距離を一周で割った余りで求めます
5回目の追いつきまでにBは10cm×5=50cm移動します。
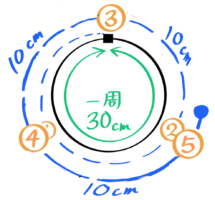
これを一周の距離30で割って50÷30=1…20 これは1周と20cmを意味するのでスタート地点から20cmと分かりますね。

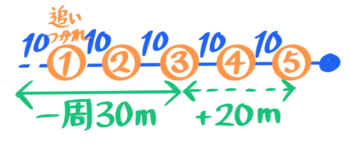
5回目の追いつかれまで10×5=50cm進み
50÷30=1…20より1周して20cmのところ
特殊な追いつき場所
例えば「Bがスタート地点で5回目に追い越される」時間を求める場合です。
Bは10cm進むごとに追い越されるので、3回目の追い越しは10×3=30m進んだ、ちょうど一周まわってスタート地点に戻ってきたところで行われます。
スタート地点で発生する
つまり、30秒ごとにスタート地点で追い越し(追い越され)ます。
よって、5回めにスタート地点で追い越す(追い越される)のは30秒×5=150秒後と分かります。
ダイヤグラム
円周上の点の動きをダイヤグラムにすると、「ぶつ切り」の平行線になります。
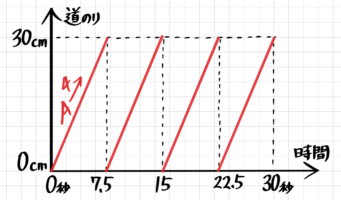
この2つのグラフを重ねて、線が交わるところが追いつきを表します。
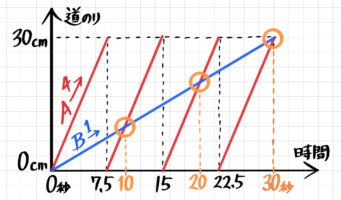
「人」型に線が交わるのが追いつくポイントです。
時間を示す横軸の数字は「10,20,30…」と、さっき出した等差数列になっています。
小まとめ
◆最初に追いつく時間(T)=一周÷速さの差
二回目以降に追いつく時間も同じ
→T×1,T×2,T×3(時間)…に追いつきを繰り返す
◆最初に追いつく距離(D)=T×速さ
ニ回目に追いつくまでの距離も同じ
→スタート地点からD×1,D×2,D×3の距離で
追い付きが繰り返される
次は円周上の出会いの旅人算です。
円周上の出会い
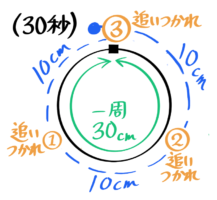
例えば、速さ3cm/秒の点Aと速さ2cm/秒の点Bが一周30cmの円周上の同じ場所から反対向きに同時に出発する場合を考えます。

一回目の出会い
出会う時間を求める~直線にする
1回目の出会いは円を開いて直線に直して考えます。
一周の距離=二人の距離になり「出会いの旅人算」と同じ図になります。

「直線上の旅人算」の公式を使って、出会う時間は30÷(3+2)=6秒後と分かります。
出会う場所を求める
ABどちらかが進んだ道のりを「速さ×時間」で計算します。遅い方で計算する方が数字が小さく簡単です。
さっき直線に開いた円を元に戻して、遅い方Bが進んだ道のりを計算します。
2cm/秒×6秒=12cmで、スタート地点から反時計回りに12cmの地点と分かります。
これで一回目の出会いの時間・場所が分かりました。
ニ回目以降の出会い→周期で考える
出会い時間の周期
実は、二回目以降の出会いは、周期的に繰り返されます。
1回目の出会った後は「同じ場所から出発し反対方向に進む」という状況はスタートの時と同じです。
((図))
ですから、一回目の出会いから二回目の出会いまでも同じ時間(この場合は6秒)がかかり、二回目から三回目も同じ時間6秒かかります。
つまりAとBは6秒後,12秒後,18秒後,24秒後…に出会うのを繰り返します(6の倍数)。
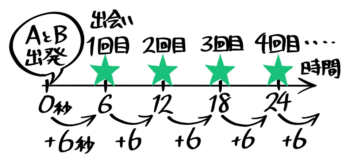
出会う地点の移り変わり
出会う地点も周期的に計算できます。
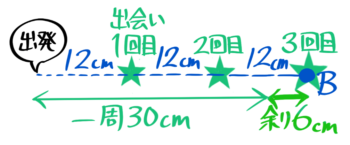
1回目の出会いが遅い方のBに注目してスタートから反時計回りに12cmの地点と分かったので、この後もBは12cmごとに出会っていくことになります。
つまり2回目の出会いはスタート地点から反時計回りに24cm,3回目は36cm,4回目は48cm…になります。
3回目の出会いは36cmですが、一周が30cmしかないので、この36cm進んだ場所は一周してから6cm進んだ地点です。
円周上のBの軌跡(左)と
それを直線状に広げたもの(右)
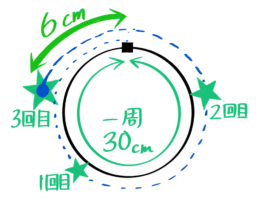
反時計回りに6cmの地点と分かる
これは36を30で割った余り6を出しているのと等しいですね。
出会いの回数で指定された場合
「8回目に出会うのはどの地点でか」のように出会いの回数で指定された場合は、上と同じように遅い方の移動距離を一周で割った余りで求めます
8回目の出会いまでにBは12×8=96cm移動しています。
これを一周の距離30で割って96÷30=3…6 これは3周と6cmを意味するのでスタート地点から6cmと分かります。
((図))
特殊な出会い場所
例えば「ちょうどスタート地点で5回目に出会う」場合を指定されることがあります。
出会い位置は12cm,24cm,36cm,48cm,60cm…と移っていました。
5回目(30秒後)の60cm地点というのが一周30cmのコースをちょうど2周したスタート地点になります。
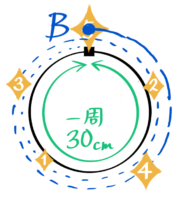
スタート地点で発生する
つまり、30秒ごとにスタート地点で出会うと分かります。
よって5回めにスタート地点で出会うのは30×5=150秒後とわかります。
円周上の出会いのダイヤグラム
円周上の旅人算をダイヤグラムにすると「ぶつ切り」の平行線になります。
「X」型に線が交わるのが出会いのポイントです。
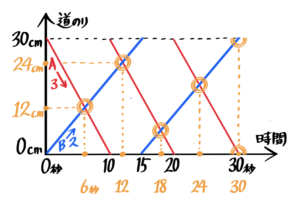
出会いポイントを見ると、時間は6秒の倍数に、場所はスタート地点から反時計回りに12cmの倍数の位置(を30で割った余り)になっているのが分かります。
速さの差を使う場合
直線上の旅人算の出会いで「速さの差」を使うパターンがありました。
円周上の出会いでも同じパターンがあります。
例えば、一周の距離が分からない円周状のコースで速さ5cm/秒のCが同時に反対向きに出発した速さが分からないDと4秒後に一周のちょうど真ん中から6cm先で出会った時に、Dの速さと一周の距離を考えます。
((円の図))
直線に直して考えると、二人が進んだ距離の差は6×2=12cmと分かります(Cの方がDより長い)。
((円の図→線にして並べた図))
「引き離し」の公式「引き離される時間=2人の距離÷速さの差」を使うと、4=12÷速さの差 より 速さの差=3なので、Dの速さは5ー3=2cm/秒と分かります。
さらに、速さ5cm/秒と2cm/秒の2人が4秒後に出会ったので一周の距離=(5+2)×4=28cmと分かります。
((完成図))
速さの和と差を使う問題
同じコースを同一地点から同時に反対方向に出発すると○分ですれ違い、同じ方向に出発すると○分で追い越す
速さの和と差が出るので、和差算でそれぞれの速さを出す。
小まとめ
◆最初に出会う時間(T)=一周÷速さの和
次に出会うまでの時間も同じ
→T×1,T×2,T×3(時間)…に出会いを繰り返す
◆最初に出会う距離(D)=T×速さ
次に出会うまでの距離も同じ
→スタート地点からD×1,D×2,D×3…
の地点で出会う
◆速さの差を使う場合
(最初の出会い場所と中央地点との差がN)
→2人の道のりの差はN×2なので、
N×2だけ「引き離した」と考えられる
速さの差=N×2÷出会った(引き離した)時間
円周の反対側からスタートする場合
円周の反対側からスタートする場合、1回目の出会い・追いつきが変わります。
((図&図))
円周上の追い付き(反対側からスタート)
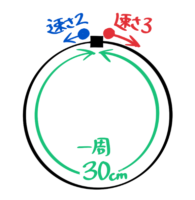
例えば、速さ3cm/秒の点Aと速さ2cm/秒の点Bが一周30cmの円周上のちょうど反対側の2地点から同じ向きに同時に出発する場合です。
(数字つきの図)
2点の距離は一周の半分15なので、最初の追いつきは距離15の「追いつく」旅人算の式で15÷(3-2)=15秒後です。
一回追いついた後は、同じ地点からスタートした場合と同じく距離30の「追いつく」旅人算なので、さっきと同じく30÷(3-2)=30秒ごとに出会います。
つまり反対側からスタートする場合は、15,45,75,105秒後に出会うのを繰り返します(はじめの数15,公差30の等差数列です)。
ダイヤグラム
作成中(2021.1)
小まとめ
◆最初に追いつく時間(t)=半周÷速さの差
二回目以降に追いつく時間(T)=一周÷速さの差
→t,t+T,t+T+T(時間)…に追いつきを繰り返す
(はじめの数t,公差Tの等差数列)
◆最初に追いつく距離(d)=t×速さ
二回目の追いつきまでの距離(D)=T×速さ
→スタート地点からd,d+D,d+D+D…
の地点で追い付きが繰り返される
(はじめの数d,公差Dの等差数列)
円周上の出会い(反対側からスタート)
同じ地点でなく、ちょうど反対側からスタートする場合も覚えておきましょう(後で出てくる「往復の旅人算」を理解しやすくなります)
(図)
例えば、速さ3cm/秒の点Aと速さ2cm/秒の点Bが一周30cmの円周上のちょうど反対側の2地点から反対向きに同時に出発する場合です。
(数字つきの図)
2点の距離は一周の半分15なので、最初の出会いは距離15の「出会う」旅人算の式で15÷(3+2)=3秒後です。
この後は距離30の「出会う」旅人算なので、さっきと同じく30÷(3+2)=6秒ごとに出会います。
つまり反対側からスタートする場合は、3,9,15,21秒後に出会うのを繰り返します(はじめの数3,公差6の等差数列です)。
出会い(反対側スタート)のダイヤグラム
作成中(2021.1)
小まとめ
◆最初に出会う時間(t)=半周÷速さの和
二回目以降に出会う時間(T)=一周÷速さの和
→t,t+T,t+T+T(時間)…に出会いを繰り返す
(はじめの数t,公差Tの等差数列)
◆最初に出会う地点(d)=t×速さ
二回目以降に出会うまでの距離(D)=T×速さ
→スタート地点からd,d+D,d+D+D…
の地点で出会いを繰り返す
(はじめの数d,公差Dの等差数列)
三人の旅人算
ここまではAとBの二人が出会ったり追いついたりしていましたが、さらに3人目のCが加わる場合です。
((図))
往復の旅人算
同じ地点・または反対側から出発した2人のうち片方または両方が折り返して出会ったり追いついたりする問題。
例えば15離れた2点PQ間を速さ4cm/秒のAと速さ1cm/秒のBが行ったり来たりします。
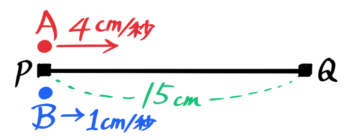
AとBが出会ったり追いついたりする時間や場所を考えますが…
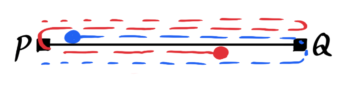
非常~に分かりづらい!!
考えただけで…頭がゴチャゴチャしてきますね。
ところが!ある工夫をするだけで、かなり分かりやすくなるんですよ!
コツ…「○」に変える!
それは「直線上の往復」を「円周上の旅人算」に変えることです♪
道のりの真ん中に切れ目を入れて、上下に広げると…つぶれた円(だ円:オーバル)のようになりました♪
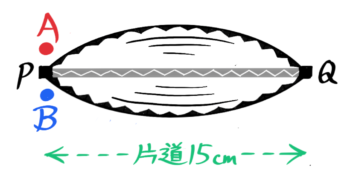
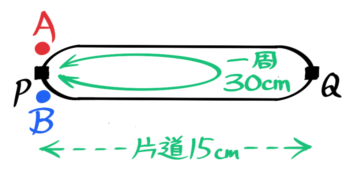
この道は一周が往復分(片道分×2)なので、一周30cmの円になります。この円を一方向にぐるぐる回ると考えます。
この状態からは、AとBが回る方向を同じにした図と反対にした図の2種類を作れます。
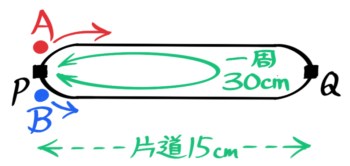
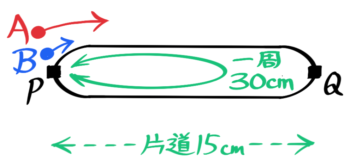
反対方向に回る図にすると出会いの様子を、同じ方向に回る図にすると追いつきの様子を調べることができます。




これで「円周の旅人算」で解くことができますね!
→往復の長さを一周とするだ円に直す

↓

この後は、同じ場所から出発する場合と反対側から出発する場合で分けて考えます。
同じ場所から出発する場合
1周30cmの円の同じ場所からスタートする円周の旅人算と考えます。
((直線図→円周図))
ここから更に、「追いつき」を考える場合と「出会い」を考える場合に分けて考えます。
「追いつき」を考える
「追いつき」を考える場合は、円に直した道をABが同じ方向に出発すると考えます。
((図))
この後は円周の旅人算と同様に考えます。
一度目の追いつきは30÷(4-1)=10秒後で、遅い方のBが1×10=10cm進んだところで発生します。
((図))
二度目からの出会いは、10秒ごと(Bが10cm進むごと)に周期的に発生するのも円周の場合と同じです。
((時間周期図&Bの軌跡と出会い))
この周期を使えば追いつきの問題を解けますね。
例えば、5回目の追いつきは10×5=50秒後、Bが1×50=50cm進んだ場所(これは50÷30=1…20で、スタート地点から20cm進んだところ)で発生すると分かります。
出会いを考える
基本解法(速さの和を使う)
出会いを考える場合は、円に直した道をABが反対側に出発すると考えます。
((図))
この後は円周の旅人算と同様に考えます。
一度目の出会いは30÷(4+1)=6秒後で、遅い方のBは1×6=6cm進んでいます。
((一度目の出会いの図))
二度目の出会いからは、6秒ごと(Bが6cm進むごと)に周期的に発生するのも円周の場合と同じです。
この周期を使えば出会いの問題を解けますね。
例えば、5回目の出会いは6×5=30秒後、Bが1×30=30cm進んだ場所(ちょうど1周してスタート地点に戻った所)で発生すると分かります。
((30秒後の図))
速さの差を使う問題
全体の道のりが分からず、一回目の出会いの場所が「折返し」からの距離で示された場合です。
例えば、距離が分からないRS間を同時にRを出発して往復する速さ5のCが速さが分からないDと4秒後に折返し(S)から6cm先で出会った時のDの速さとRS間の距離を考えます。
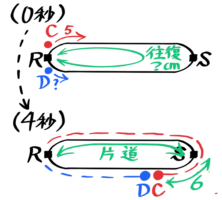
円に直して考えると、二人が進んだ距離の差は6×2=12cmと分かります(Cの方がDより長い)。
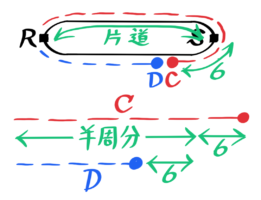
なので差は12と分かる
「引き離し」の公式「引き離される時間=2人の距離÷速さの差」を使うと、4=12÷速さの差 なので速さの差=3と分かり、Dの速さは5ー3=2cm/秒と分かります。
さらに、速さ5cm/秒と2cm/秒の2人が4秒後に出会ったので円に直した往復の距離=(5+2)×4=28cm、片道(RS)は14cmと分かります。
((完成図))
ダイヤグラム
2回追いつくまでに何回出会うか?のように、出会いと追いつき両方を考える場合は、ダイヤグラムを使います。
往復旅人算のダイヤグラム
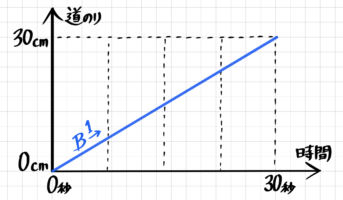
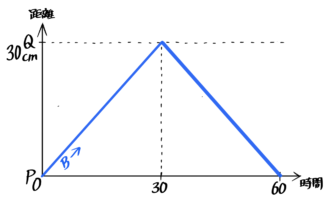
例えば30離れた2点PQ間を速さ4cm/秒のAと速さ1cm/秒のBが往復する場合を考えます。
Aは片道7.5秒往復15秒、Bは片道30秒往復60秒かかります。遅いBが往復する60秒間のAのダイヤグラムとBのダイヤグラムは次のようになります。
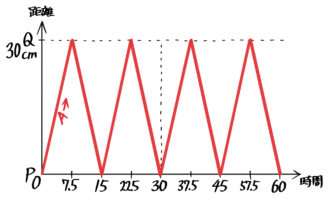
これを重ねると「往復の旅人算のダイヤグラム」になります。
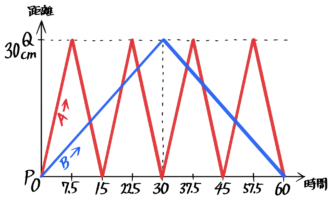
グラフが「>」型で交わるのが出会い、「∧」「∨」型で交わるのが追いつきです。
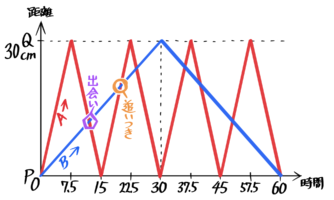
この時に、後の問題に備えて出会いと追いつきの周期を出してしまうと良いでしょう。
出会いは、一周60cmの円周(オーバル)の出会いと考えて計算します。時間は一回目の出会いが60÷(4+1)=12秒後で、以降も12秒ごとにAとBは出会います。場所は遅い方のBで計算すると1回目の出会いが1×12=12cm地点で、以降もBが12cm進むごとに出会います。
追いつきは一周60cmの円周(オーバル)の追いつきと考えて計算します。時間は一回目の追いつきが60÷(4-1)=20秒後で、以降も20秒ごとにAがBを追い越します。場所は遅い方のBで計算すると1回目の追い越し(追い越され)1×20=20cm地点で、以降もBが20cm進むごとにAに追い越されます。
出会いと追いつきの回数
他の場合のダイヤグラムと同じで、出会いは「>」型に交わる所で、追いつきは「∧」型に交わるところです。

これを使うと、2回追いつくまでに3回出会ったと分かります。
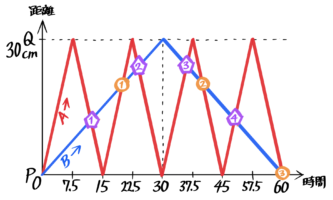
出会いと追いつきの場所・時間
回数が分かれば、場所や時間は上で見たような周期の問題として解くことができます。
例えば「2回追いついた後の最初の出会いの位置と時間を聞かれた場合」、
ダイヤグラムから「2回追いついた後の最初の出会い」が始めから数えて4回目の出会いと分かります。
そして出会いの周期(12秒ごと/Bが12cm進むごと)から、4回目の出会いは12×4=48秒後、場所はBが12×4=Pから48cm進んだ地点で、これは60-48=12からスタート地点Pまであと12cmのところと分かります。
反対側から出発する場合
反対側からスタートする円周の旅人算と考える。
((直線図→円周図))
ここから更に、問題文が「出会い」について聞いている場合と「追いつき」について聞いている場合に分けて考えます。
追いつき
一度目の追いつきは、円周の半分(=片道)15÷(3-2)=15秒後に、遅い方のBが2×15=30cm進んだ地点(つまりP)で発生します。
二度目からの出会いは、同じ地点から出発したのと同じ30÷(3-2)=30秒、遅い方のBが2×30=60cm進む周期で発生します。
つまり、出会いの時間は15,45,75,105…秒後という「はじめの数15、差が30の等差数列」になり、出会いの場所は遅い方のBが30,90,150,210…進んだ地点という「はじめの数30、差が60の等差数列」になります。
出会い
速さの和を使う
一度目の出会いは、円周の半分(=片道)15÷(3+2)=3秒後に、遅い方のBが2×3=6cm進んだ地点で発生します。
二度目からの出会いは、同じ地点から出発したのと同じ30÷(3+2)=6秒、遅い方のBが2×6=12cm進む周期で発生します。
つまり、出会いの時間は3,9,15,21…秒後という「はじめの数3、差が6の等差数列」になり、出会いの場所は遅い方のBが6,18,30,42…進んだ地点という「はじめの数6、差が12の等差数列」になります。
速さの差を使う
同地点からスタート
片道2回分の等時間隔で出会ったり追いついたりを繰り返します。
一回目の出会い(折り返して出会い)
折返しコースのマラソン大会で足の速いAが先に折り返して遅いBとすれ違うような場合です。
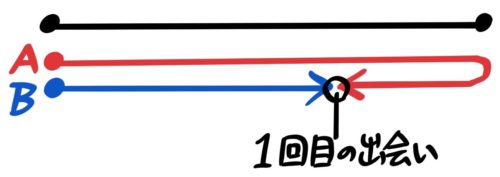
(マラソン大会のイメージ)
このパターンは2つの利用法があります。
和を利用
コースの長さが分かっているような場合は、ABが進んだ道のり全体を一直線に伸ばします。
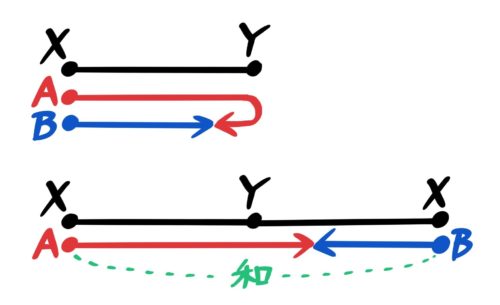
コース2つ分はなれた出会いの旅人算になる
例えば10cmのコースを点Aが3cm/秒で点Bが2cm/秒で同時に出発した場合、コース2つ分(20cm)はなれたABの出会いになるので、20÷(3+2)=4秒後に出会います。
出会う場所は速さ2のBが4秒進んだ場所なのでスタートから2×4=8cm地点です。
差を利用
コースの長さが分からずABが出会った地点が分かっている場合はAだけを一直線に伸ばします。
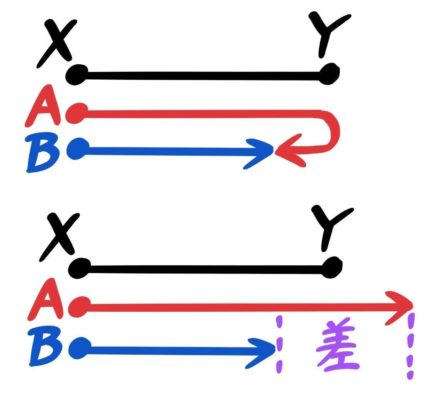
追い付き(引き離し)の旅人算になる
例えばXY間のコースを点Aが3cm/秒で点Bが2cm/秒で同時に出発して、ABがYから2cm手前ですれ違った場合、伸ばしたAはBより2cm×2=4cm長くなります。
AとBの差が4cmになる「引き離し」の旅人算なので4÷(3-2)=4秒後に出会ったと分かります。
そしてコースの片道は速さ2のBが4秒進んだ2×4=8cmに2cm足した10cmです。
二回目以降の出会い
等時間隔で出会う
一回目の出会いの後、二人が進んだ道のりの和が「片道2回分」になるごとに(等間隔の時間ごとに)出会います。
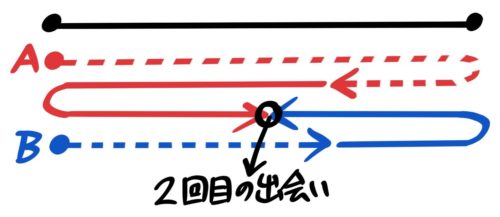
1回目の出会いも2人の和が片道2回分ので、このパターンではスタートからずっと等間隔の時間で出会うことになります。
上の例(片道10cmのコースを3cm/秒のAと2cm/秒のB)だと、一回目に出会うのが(10+10)÷(3+2)=4秒で、ニ回目はその4秒後の8秒、つまり4,8,12秒ごとに出会います。
出会う位置
出会う位置を出す時はABどちらかを基準にして(遅いBの方が計算が簡単)4秒,8秒,12秒の位置を出します。
4秒後は2×4でスタートから8cm地点、8秒後は2×8=16cmでスタート地点の手前4cm地点です。12秒後は2×12=24cmでスタート地点を過ぎて4cm地点です。
つまり出会う位置は2×4=8ずつ「Bの進行方向に」ずれていくと分かります。
時間差で出発して一回目の追い付き
これは基本の旅人算の追い付きです。
同時出発して一回目の追い付き
2人の速さの関係によって状況が異なりますが、二人が進んだ道のりの差は「片道2回分」になります。
円周上の道(校庭のトラック)を速い方(A)が一周多く走って遅い人(B)に追いつくイメージです。
二回目以降の追い付き
二人の進んだ道のりの差が「片道2回分」になるごとに(等間隔の時間ごとに)出会う。
反対側からスタート
1回目の出会い・追い付きは「片道1回分」の時間で、二回目以降の出会い・追い付きは「片道2回分」の等時間隔で繰り返されます。
一回目の出会い
基本の旅人算の出会い。二人の進んだ道のりの和が「片道1回分」の時に出会う
ニ回目以降の出会い
一回目の後、二人の進んだ道のりの和が「片道2回分」になるごとに出会う。(同じ地点から出発した場合と同じ)
一回目の追い付き
2人の速さの関係によって状況は異なるが、二人の進んだ道のりの差が「片道1回分」の時に追いつく
二回目以降の追い付き
一回目の後、二人の進んだ道のりの差が「片道2回分」になるごとに追いつく。(同じ地点から出発した場合と同じ)
 爽茶
爽茶●
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。