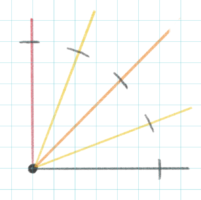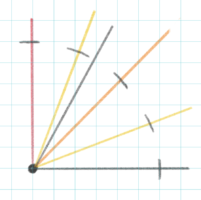「図形が回る問題が苦手!」という中学受験生の方へ
確かに図を上手に書こうとすると難しいですが、「イメージ」できれば答えを出す計算は複雑ではありませんし、入試でもよく出るので得意にしてしまいましょう♪
この記事では、東大卒講師歴20年超の図解講師「そうちゃ」が図形の回転移動の基礎から応用まで分かりやすく説明します
記事を読んで例題が解ければ、回転移動の問題は得意になっているでしょう
目次(クリックでジャンプ)
回転移動とは
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
はじめに回転移動について簡単に説明します。平行移動と回転移動
図形(線、面)の移動には大きく分けて➀平行移動と②回転移動 があります
中心
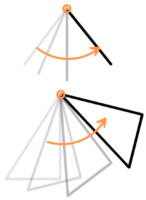
中心に向きを変える
この記事で扱う回転移動は向きを変える移動で、もう一方の平行移動は向きを変えない移動方法です(平行移動については関連記事「図形の平行移動」を見て下さい)
また、中心を変えながら回転していく「転がり運動」については「多角形の転がり」や「円おうぎの転がり」を見て下さい(下図はおうぎ形の転がり)
円おうぎを描く練習
「回転移動」や「転がり移動」では円周や弧を書くことが多いので、ここで円やおうぎ形を描く練習をしてみましょう
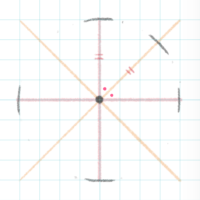
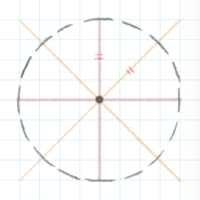
円を描く
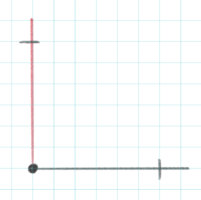
①まず中心を決めます
②中心から上下左右の直線を意識して半径の長さの位置に短い線を引きます
線と半径を垂直にします。また長めの線を引くときは少しカーブさせます。
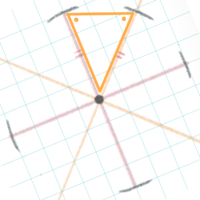
③上下左右の線を2等分するように線をイメージして(45度の角度)をイメージして、その上に半径と同じ長さの線を引きます。
半径と同じ長さをとるコツは、紙を回転させて二等辺三角形を作ることをイメージすること
半径と直角に引くのと、長い線は少しカーブさせるのも忘れずに。
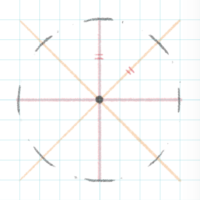
これを繰り返して4方向(右上,右下,左下,左上)に線を引きます
一つ一つ二等辺三角形を作るのが面倒なら、紙を傾けて左右対称を使ってもOK♪
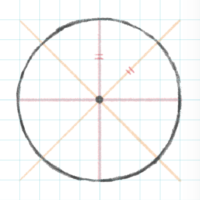
これで8方向に短い線が描けました
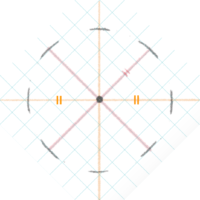
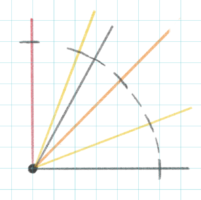
④線の間にも短い線を描いて、点線の円を作ります
このときも長い線は少しカーブさせると良い
⑤点線をつなげる感じで、濃い線で清書します
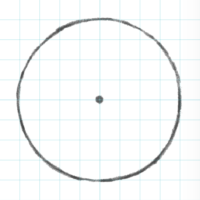
⑥完成した円
おうぎ形を描く
試しに60°のおうぎ形を書いてみます
①おうぎ形の方向に半径と基準線を書き、半径の長さをとる
②45°線と、さらに間の線を引き、半径で区切る
これで基準となる円ができました
③中心角を考えて2つ目の半径を書く
60°なら45°と90°の真ん中の線(45+90)÷2=67.5°より少し手前あたりにテキトーに書く
テキトーがいやな人は1時ちょうどの時計の短針の角度で
④区切り線の間に線を引く
⑤濃く太い線で清書
⑥余分な線を消して完成
点の回転移動
 爽茶
爽茶点の回転移動とは、例えばこんな問題です。
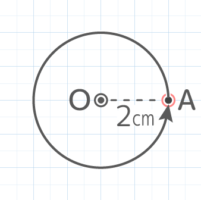
X-1:点の回転
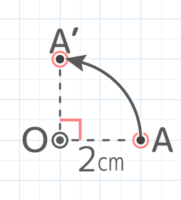
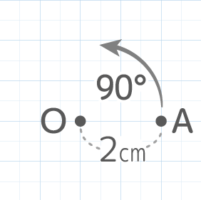
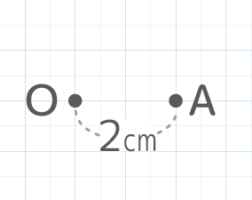 図の点Aを点Oを中心に回転させるとき、以下の問いに答えなさい(SSHT2023)
図の点Aを点Oを中心に回転させるとき、以下の問いに答えなさい(SSHT2023)Y[予5上8例題2補完]

ヒント
(ここにヒントが入ります)
解説
ヒント
(ここにヒントが入ります)
解説
練習問題(23.4.24作成中)
小まとめ
●360度の回転→円を描く
●360度未満の回転→弧を描く
線の回転移動
 爽茶
爽茶線の回転移動は「回転の中心」の位置によって色々な図形が出来ます。
①回転の中心が線(の延長)上にある場合
② 〃 ない場合
で考え方が大きく変わります
回転中心が線(の延長)上にある場合
回転の中心が端にある場合
こんな問題です
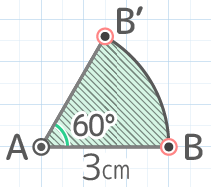
X-1:線の回転(端を中心)
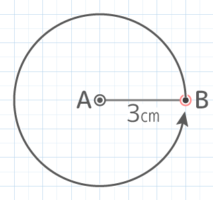
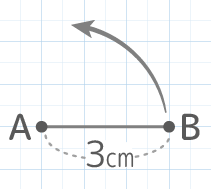 3cmの線分ABをAを中心に回転させるとき次の問いに答えなさい
3cmの線分ABをAを中心に回転させるとき次の問いに答えなさいY[予5上8例題2補完][予5上8基本1(4)]
ヒント
重りのついたヒモを振り回すイメージ?
解説
ヒント
腕を60°上げるイメージ?
解説
練習問題(23年度中に補充予定)
回転の中心が線の途中にある場合
できる図形ががさっきと少し変わります
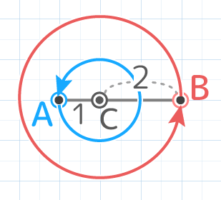
X-1:線の回転(途中を中心)
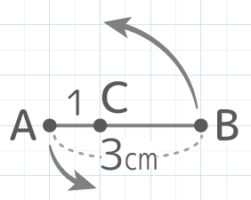 3cmの長さの線分ABがAから1cmの点Cを中心に回転するとき、次の問いに答えよ(SSHT2023)
3cmの長さの線分ABがAから1cmの点Cを中心に回転するとき、次の問いに答えよ(SSHT2023)ヒント
(ここにヒントが入ります)
解説
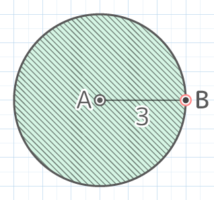
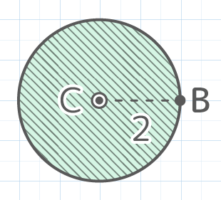
AとBがCを中心に回転するとAは半径1cmの円を、Bは半径2cmの円を描くので
回転の跡(軌跡)は線分CBが360°回転したのと等しく半径2cmの円になる
よって面積は2x2x3.14=12.56cm2 と分かる
ヒント
(ここにヒントが入ります)
解説
練習問題(2023年度中に補充予定)
線の延長線上にある場合
X-1:線の回転(途中を中心)
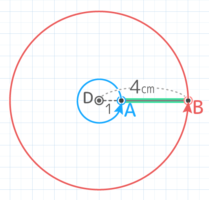
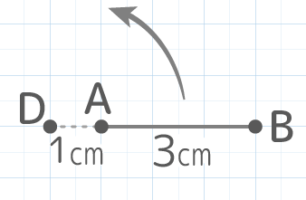 3cmの長さの線分ABがABの延長線上のAから1cmの点Dを中心に回転する時、以下の問いに答えよ(SSHT2023)
3cmの長さの線分ABがABの延長線上のAから1cmの点Dを中心に回転する時、以下の問いに答えよ(SSHT2023)ヒント
DAの部分も回ることに注意
解説
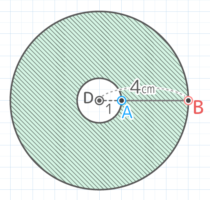
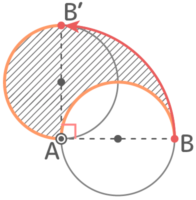
AとBがDを中心に1回転し、Aは半径1cmの円を、Bは半径4cmの円を描くので
回転の跡(軌跡)は半径4cmの円から半径1cmの円を引いた「ドーナツ形」になり
面積は (4x4x3.14)ー(1x1x3.14)=(16-1)x3.14=15×3.14=47.1cm2 になる。
ヒント
(ここにヒントが入ります)
解説
練習問題(2023年度中に補充予定)
回転中心が線(の延長)上にない場合
ここまでは回転の中心が線(の延長)上にありました。次は回転の中心が線(の延長)上にない場合で、考え方が変わります。
最近点が線の端にある場合
X-1:線の回転(外の点を中心Ⅰ)
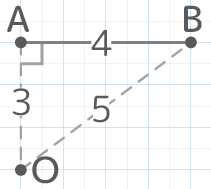
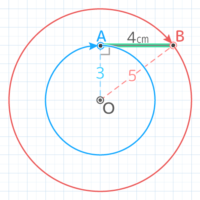
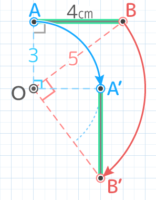
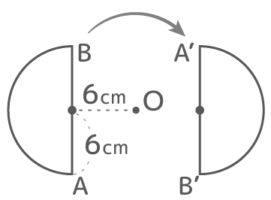
 図のように線分ABがOを中心に回転する時、以下の問いに答えなさい。
図のように線分ABがOを中心に回転する時、以下の問いに答えなさい。Y[予5上8例題2補完]
ヒント
(ここにヒントが入ります)
解説
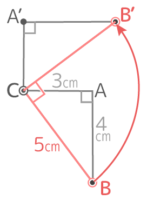
回転する前にOABは直角三角形を作りOBの長さが5cmになることを確認(3-4-5の整数直角三角形)
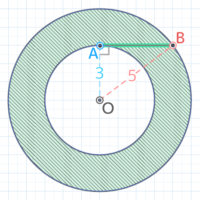
Oを中心にABを回転させると、Oに一番近い点Aは半径3cm、一番遠い点Bは半径5cmの円を描く
線分ABが移動した跡(軌跡)は2つの円に挟まれた「ドーナツ形」になる
よって面積は (5x5x3.14)-(3x3x3.14)=(25-9)x3.14=16×3.14=50.24cm2 になる♪
ヒント
(ここにヒントが入ります)
解説
練習問題(23.4.24作成中)
最近点が線の端にない場合
少しだけ難しくなります(入試に出るのはこのタイプ)
X-1:線の回転(外の点を中心Ⅱ)
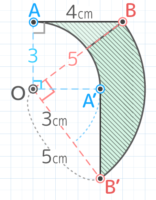
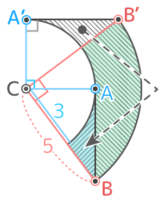
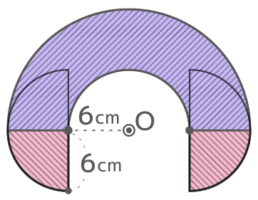
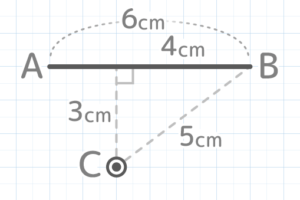 図のような6cmの長さの線分ABが点Cを中心に360°回転するとき、以下の問いに答えよ
図のような6cmの長さの線分ABが点Cを中心に360°回転するとき、以下の問いに答えよY[予5上8例題3′]
ヒント
一番近い=垂直(直角)に測った場所です
解説
3cmはCからABに向かって直角に引いた線がABと交わる点(直角マークの所)Dとの距離で、Dは直線ABでCから一番近い箇所です。
ヒント
一番近い点と一番遠い点がポイント
解説
Cは点Bとの距離は5cmで線分ABとの距離が3cmです。線との距離は直角に測ります。直角マークに注目
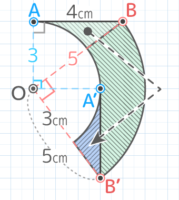
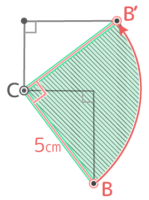
Cを中心にABを回転させると…回転の軌跡(色がついた部分)はドーナツ型で、外側の円は半径5cm、内側の円は半径3cmになっています。
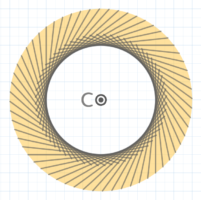
半径5cmがCBの長さで、半径3cmは線ABと点Cとの距離です。
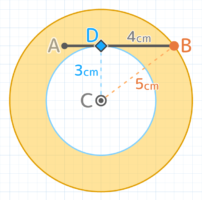
一番遠い点Bを回転させて
囲まれたドーナツ型で
点Aは埋もれている
3cmはCからABに向かって直角に引いた線がABと交わる点(直角マークの所)Dとの距離で、Dは直線ABでCから一番近い箇所です。
一方5cmは直線ABでCから一番遠いBとの距離で、CとAの距離は重要ではありません。
つまり、このドーナツ型は直線ABの中で回転の中心から一番近い点Dと一番遠い点Bを回転させて作られるのです。
そして軌跡の面積は(5×5×3.14)-(3×3×3.14)=(25-9)×3.14=50.24cm2と分かります♪
このように、回転の中心が直線(の延長線)上にない場合は、回転の中心から一番近い点と一番遠い点を回転させれば軌跡が分かります。
練習問題(23.4.24作成中)
折れ線の回転
曲線の回転
三角形の回転移動
 爽茶
爽茶角度の問題
まず回転移動する場合の角度を考えます。
ポイントは、回転移動では形が変わらないので合同(長さも角度も等しい)な図形ができているということ
例題を解いてみましょう
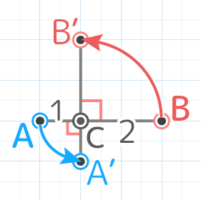
X-1:三角形の回転と角度
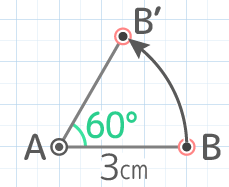
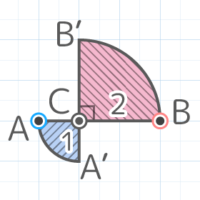
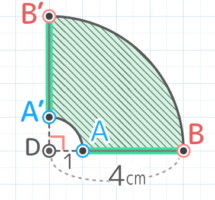
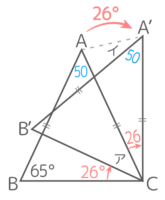
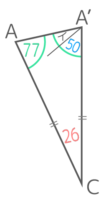
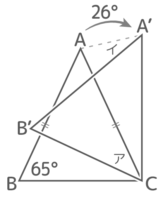 図のような二等辺三角形ABCをCを中心に時計回りに26°回転させたところA’B’Cに移った。角度ア,イは何度か
図のような二等辺三角形ABCをCを中心に時計回りに26°回転させたところA’B’Cに移った。角度ア,イは何度かY[予5上8例題1′][予5上8基本1(1)][予5上8基本2]
ヒント
合同(長さも角度も同じ)の性質を利用する
解説
練習問題(作成検討中)
移動の跡(軌跡)の問題
面の回転移動の問題は、これまで見てきた点・線・折れ線の回転移動を含んでいて、全く同じように解けます。
例えばこんな問題です
X-1:三角形の回転移動
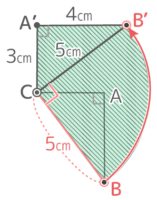
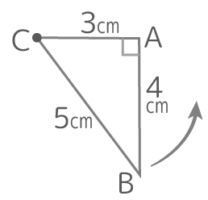 直角三角形ABCをCを中心に90°回転させるとき、以下の問いに答えなさい
直角三角形ABCをCを中心に90°回転させるとき、以下の問いに答えなさいY[予5上8例題2′][予5上8基本1(5)][予5上8基本4][予5上8練習1][予5上8練習2]
ヒント
○の回転と同じ
解説
これは「点の回転」と同じで動いた跡(軌跡)は円や弧になる
この場合、半径5cm中心角90°の弧になるので、その長さは 5x2x3.14x90360=2.5×3.14=7.85cm と求められる♪
ヒント
今度は「○の回転」と同じ
解説
辺の回転は「線の回転」と同じで、この場合は線の端を中心に回転するので、軌跡は半径5cm中心角90°のおうぎ形になる
よって面積は 5x5x3.14x90360=254x3.14=6.25×3.14=19.625cm2 と求められる♪
ヒント
回転の中心の位置に気をつける
解説
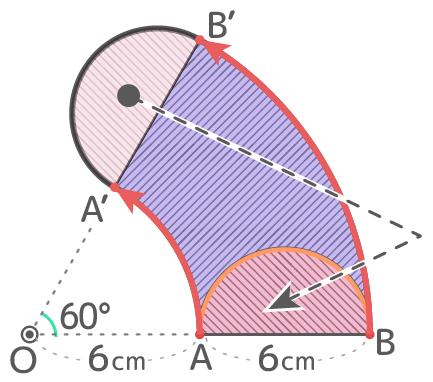
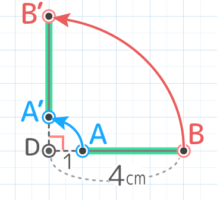
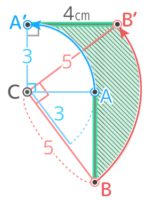
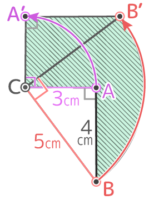
これも辺の軌跡だが、中心の回転が辺(の延長線)上にないので軌跡は少し複雑(辺AB、弧BB’、辺A’B’、弧AA’に囲まれた部分)になるが…
上の部分を左下に移すと、内側の半径3cm,外側の半径5cm,中心角90°の「バームクーヘン形」になる
よって面積は (5x5x3.14x90360)- (3x3x3.14x90360)=4×3.14=12.56cm2 と求められる。
ヒント
落ち着いてイメージします
解説
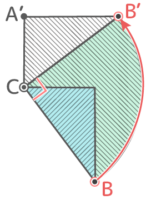
ABC全体が動いた跡を想像すると、こうなる
これは元の三角形ABC(面積3×4÷2=6)と90°のおうぎ形(これは(2)の答え:19.625そのまま)をあわせたものなので、面積は 6+19.625=25.625cm2 と求められる♪
ヒント
○○線の回転と同様
解説
練習問題(2023.4.19作成中)
(正)(長)方形の回転移動
長方形の回転移動の問題では、対角線を加えると直角三角形の回転と同じに解けます。
例えば、縦3cm横4cmの長方形を90°回転させる問題は、先程の三辺が3cm,4cm,5cmの直角三角形を回転させたのと同じになっています。
計算が少し面倒な練習問題をどうぞ
X-1:長方形の回転移動
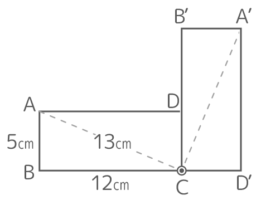
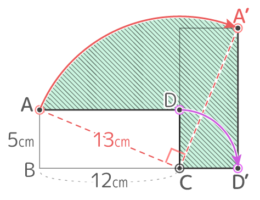
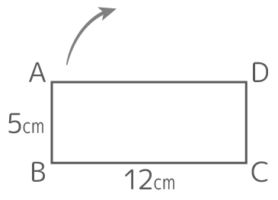 図のような長方形ABCDを点Cを中心に90°回転させるとき、以下の問いに答えなさい。この長方形の対角線の長さは13cmです。
図のような長方形ABCDを点Cを中心に90°回転させるとき、以下の問いに答えなさい。この長方形の対角線の長さは13cmです。Y[予5上10(総合)練習1′]
ヒント
(ここにヒントが入ります)
解説
対角線が13cmなので、3辺が5cm,12cm,13cmの直角三角形ABCを90°回転させたのと似ている
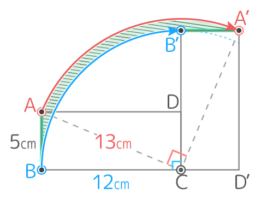
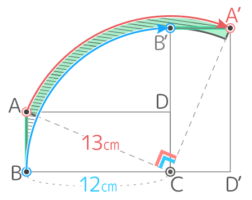
辺ABの回転移動はした跡は下図のような、辺AB,弧BB’,辺B’A’,弧A’Aに囲まれた形になる。
この形の左端(対角線CAで左に切り落とされる部分)を右上に移すと、外径13cm,内径12cmの「ドーナツ形」になる
よって面積は (13x13x3.14x14)-(12x12x3.14x14)=(13×13-12×12)x3.14x14=254x3.14=6.25×3.14=19.625cm2 と求められる
ヒント
(ここにヒントが入ります)
解説
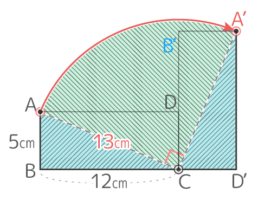
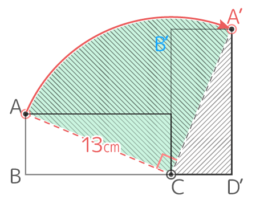
長方形全体が動いた跡は図のようになる
この形は対角線で半分にされた長方形が2個(つまり長方形1個分)と半径13cmの四半円の合計になっている。
よって面積は (12×5)+(13x13x3.14x14)=60+(42.25×3.14)=60+132.665=192.665cm2 と求められる
ヒント
(ここにヒントが入ります)
解説
多角形の回転移動は以上です。
円の回転移動
「回転の中心」の位置によって結果が変わります
((3つの場合のGIFアニメ))
回転の中心が円周上にある
5-1:円の回転
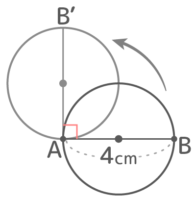
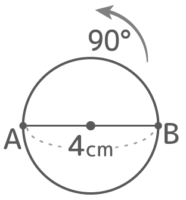 直径4cmの円を直径の一方の端Aを中心に90度回転させるとき、以下の問いに答えなさい
直径4cmの円を直径の一方の端Aを中心に90度回転させるとき、以下の問いに答えなさいY[予5上9基本1(5)’]
ヒント
点Bの動きを考える
解説
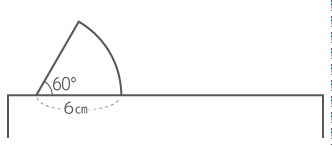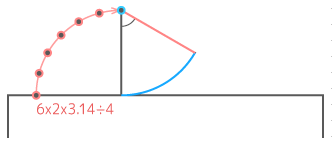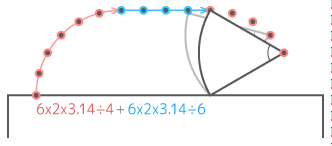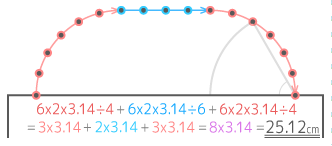
Aを中心に90度回転させると、直径ABが90度回転したAB’を直径とする円ができる
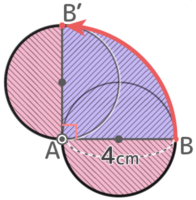
円全体が移動した跡は図のようになる
これは半径2cmの半円が2つ(つまり半径2cmの円が1つ)と半径4cmの四半円が1つの合計なので、面積は
(2x2x3.14)+(4x4x3.14x14)=(4+4)x3.14=8×3.14=25.12cm2
となる。
ヒント
形が分かったら整理する
解説
回転の中心が内部にある
回転の中心が外部にある
おうぎ形の回転移動
円の場合と同様「回転の中心」の場所によって、結果が変わります
回転の中心がおうぎ形上にある
6-1:おうぎ形の回転Ⅰ
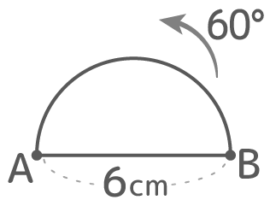 図のように半円の直径の一方の端Aを中心に60度回転させるとき、以下の問いに答えなさい
図のように半円の直径の一方の端Aを中心に60度回転させるとき、以下の問いに答えなさいY[予5上9例題1′] [予5上9基本3][予5上9練習5][予5上10(総合)基本10]
ヒント
Bの動きに注目
解説
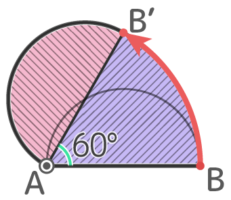
Aを中心に60度回転させると、直径ABが60度回転したAB’を直径とする半円ができる
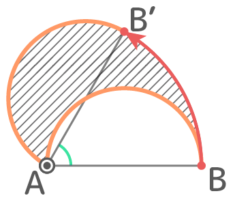
この半円全体が移動した跡は図のようになる
この跡は半径6cmの半円と半径6cm中心角60度のおうぎ形の合計なので、面積は
(6x6x3.14x16)+(6x6x3.14x12)=(6+18)x3.14=24×3.14=75.36cm2
となる。
ヒント
複雑な形の面積は単純な形を足したり引いたりして求める
解説
分かりましたか?
回転の中心がおうぎ形上にない
6-2:おうぎ形の回転Ⅱ
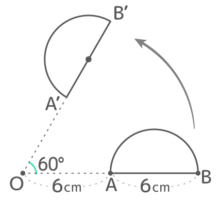
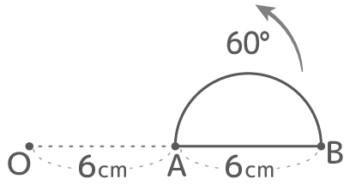 図のように半円を直径の延長線上にある点Oを中心に60度回転させたとき、次の問いに答えよ
図のように半円を直径の延長線上にある点Oを中心に60度回転させたとき、次の問いに答えよY[予5上9回 補完A]
ヒント
(ここにヒントが入ります)
解説
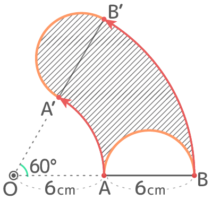
半円が移動すると、AとBが回転移動したA’B’を直径とする半円になる。
このとき半円全体が移動した跡は下図のようになる
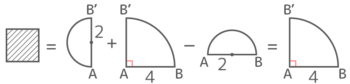
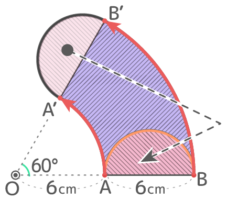
これは半径3cmの半円と「内側の半径が6cm,外側の半径が12cm,中心角が60°のバームクーヘン」の合計だから
(3x3x3.14÷2)+{(12x12x3.14-6x6x3.14)x60360}
=4.5x3.14+18×3.14=22.5×3.14=70.65cm2
となる。
ヒント
(ここにヒントが入ります)
解説
分かりましたか?
次は、少しイメージしづらい問題です。
6-3:おうぎ形の回転(難)
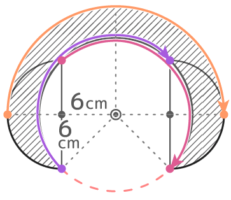
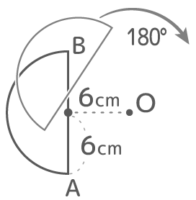 図のように半円を点Oを中心に180度回転させるとき次の問いに答えなさい
図のように半円を点Oを中心に180度回転させるとき次の問いに答えなさいY[予5上9練習1′]
ヒント
(ここにヒントが入ります)
解説
直径ABが180°回転してA’B’に移るので、半円全体はA’B’を直径とする半円に移る
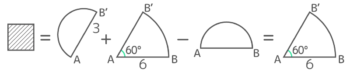
このとき、半円が動いた跡の面積は下図のようになる
これは2つの図形に分けられる。
一つは、半円上の点で回転の中心Oに一番近い点までの距離6cmを内側の半径,一番遠い点までの距離12cmを外側の半径にする中心角180°のバームクーヘン形。もう1つは半径6cmの四半2つ=半円。
これらを合計すると、
{(12x12x3.14-6x6x3.14)x180360}+(6x6x3.14x180360)=(54+18)x3.14=72×3.14=226.08cm2
になる。
ヒント
弧の中で、回転の中心から一番近い場所と遠い場所を探します
解説
弧の上の点の中で、回転の中心から一番近いのはAとB点・遠い点は弧の真ん中の点です。
これらを180°回すと弧が動いた跡の輪郭ができます♪
外側は弧の半分と半径12cmの半円を合わせた形、内側は半径6cmの円の34になります。
ヒント
面積が求めやすいように分割して足して引く
解説
斜線を一発で出すのは無理なので、足し引きで考える。
ここでは「半径12cmの半円+半径6cmの四半円2つ+等辺6cmの直角二等辺三角形2つ」ー「1辺6cmの正方形の対角線を半径とする円の34」で出せる。
「1辺6cmの正方形の対角線を半径とする円」の半径そのものは分からないが、6×6=36=半径x半径÷2なので半径x半径=72とわかる。
よって弧が移動した跡の面積は「半径12cmの半円+等辺6cmの直角二等辺三角形2つ-半径x半径が72の円の34」と等しいので、面積は
(12x12x3.14x180360)+(6x6x12x2)-(72×3.14x34)=(18×3.14)+(6x6x12x2)=56.52+36=92.52cm2
分かりましたか?
図形の回転移動は以上です
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。