「長方形や三角形が転がる問題」が苦手！な中学受験生の方へ
確かにイメージして何を計算するのかを求めることが難しい分野です。
しかし計算自体は実は2種類しかなく、そんなに面倒ではありません(3.14の筆算一発で出る問題も多い)
そして、何より入試によく出るので(易しめの学校でも出題される)、身に付けると志望校合格の可能性が確実に上がります。つまりコスパが良い！
だから、この機会にがんばって身につけてしまいましょう!
この記事では東大卒講師歴20年超の図解講師「そうちゃ」が長方形や三角形つまり多角形の転がり移動の問題を基礎から応用まで分かりやすく解説します。
記事を読んで例題が解けるようになれば「多角形の転がり移動」が得意になっているでしょう♪
この記事は「回転移動」の続きです。まだ読んでいない人はそちらを読むと良いでしょう
転がり移動とは
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
図形の「平行移動」は向きを変えない移動、「回転移動」は向きを変える移動でした。
「転がり移動」は回転移動の一種です。
他の図形(直線や多角形・円おうぎなど)と接している状態からスタート
接している点を中心に回転して、別の点(辺)が接したら回転が終了します。直方体の箱(ティッシュペーパーなど)を床に立てて押すと「パタッ」と倒れる動きですね
これを断続的に行うのが「転がり移動」で、算数の問題では「すべらずに移動する」と表現してあることが多いです。
長方形の直線上での転がり移動は、こんな感じです
方形の転がり移動
爽茶直線上を転がる
こんな問題です。
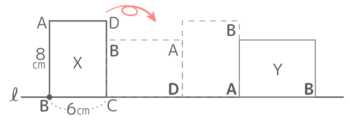
X-1:線上を転がる長方形
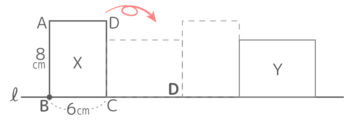
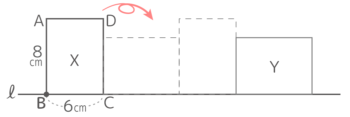図のような長方形ABCDがXの位置からYの位置まで滑らずに転がって移動するとき、点Bの移動について次の問いに答えなさいY[予5上8例題4′][予5上8基本1(3)][予5上8練習4]
ヒント
頂点の位置はコロコロ変わるように見えますが、回転しても1つだけ変わらないことがあります。
解説
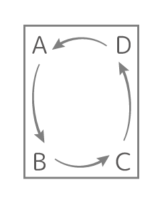
ある点の位置を探そうとしても図形が回転していると頭が混乱しがちです。そこで回転しても変わらない「頂点の順番」を利用する。
反時計回りに「A→B→C→D→A→B→C→…」という順番は変わらない。これを利用する
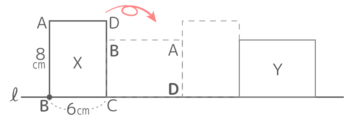
始めの転がりで地面にパタッと着くのは点D
点Dから反時計回りにD→A→BとたどるとBの位置が分かる
これをYの位置まで続ければBの位置が分かる♪
ヒント
おうぎ形の弧になります。半径と中心角を調べましょう
解説
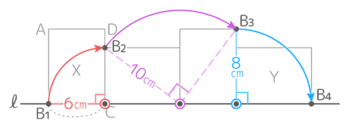
点BはまずCを中心に半径6cm中心角90°の弧を描き、つぎにDを中心に半径10cm90°の弧を、最後にAを中心に半径8cmの弧を描く
よって長さは (6x2x3.14x90360)+ (10x2x3.14x90360)+ (8x2x3.14x90360)=(3+5+4)x3.14=12×3.14=37.68cm になる
ヒント
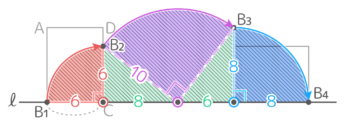
おうぎ形以外の面積に注意です
解説
Bが動いた跡と直線Lで囲まれた部分はこうなる
この形は中心角90°で半径が6cm,10cm,8cmのおうぎ形と横6cmx縦8cmの長方形の半分が2個(つまり長方形1つ)の合計になっている
よって面積は (6x6x3.14x90360)+ (10x10x3.14x90360)+ (8x8x3.14x90360)+(6×8)={(9+25+16)x3.14}+48=(50×3.14)+48=157+48=205cm2 になる
分かりましたか？
練習問題をどうぞ(2023.4.20作成中)
方形の外を転がる
X-1:方形外を転がる長方形
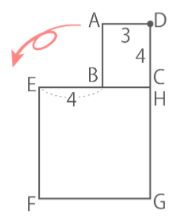図のような長方形ABCDを1辺7cmの正方形EFGHの周りを転がすとき、以下の問いに答えよ(SSHT2022)ヒント
まずDの位置を書き込みましょう
解説
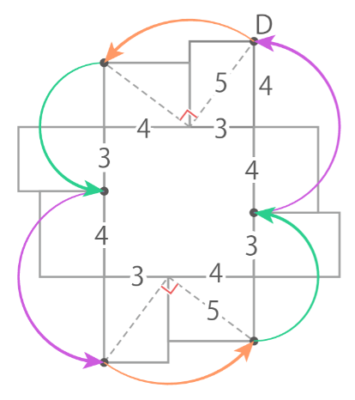
まず転がされた長方形を書き、それに移動した点Dを書き足し、中心を考えておうぎ形の弧を描く
すると半径5cm中心角90°の弧2つ、半径3cm中心角180°の弧2つ、半径4cm中心角180°の弧2つをつなげた曲線になる
ヒント
(1)ができれば、後は計算するだけですね
解説
(5x2x3.14x90360)x2+(3x2x3.14x180360)x2+(4x2x3.14x180360)x2=(5+6+8)x3.14=19×3.14=59.66cm と求められる
練習問題(23年度中に補充予定)
折れ線上を転がる
X-1:折れ線上を転がる方形
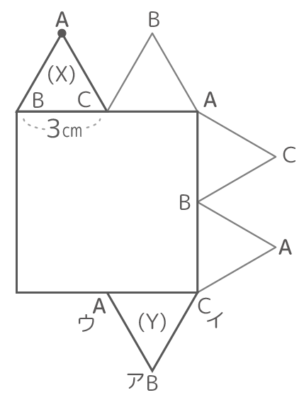
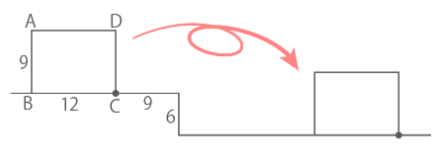長方形ABCDが図のような折れ線の上を転がってもとの向きになるとき、以下の問いに答えなさい(SSHT2022)ヒント
途中、斜めに！なります
解説
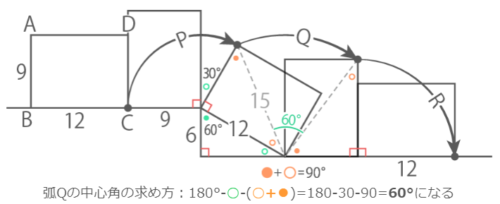
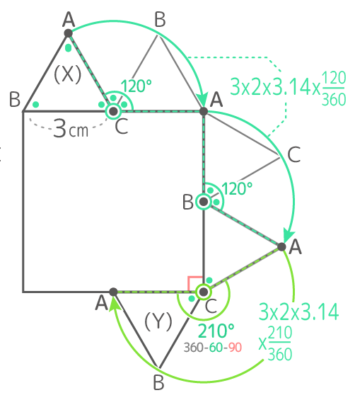
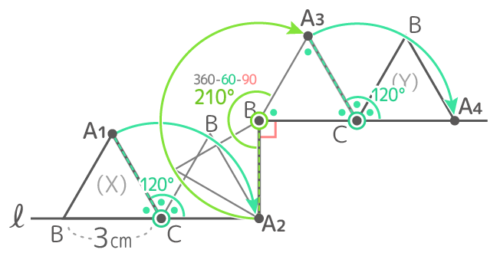
転がった長方形を(間に3つ)書き、それらに点Dを付け足して、中心に気をつけて弧を書くと下図のようになる
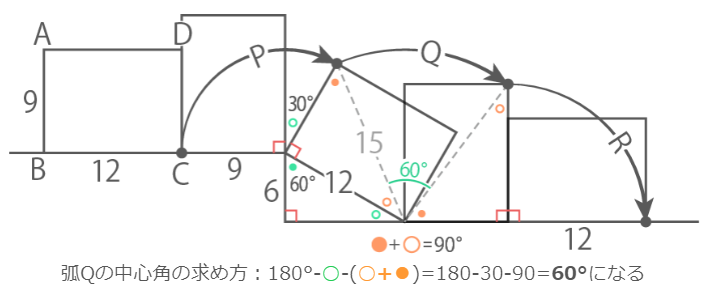
点Cが移動した跡は、半径9cm中心角120°の弧,半径15cm中心角60°の弧,半径12cm中心角90°の弧がつながったもの
3番目の状態では折れ線との間に「正三角形を半分にした三角定規」が出来るているのに注意
ヒント
(1)ができれば計算するだけです
解説
(1)よりCが動いた跡の長さは (9x2x3.14x120360)+ (9x2x3.14x120360)+ (9x2x3.14x120360)=(6+5+6)x3.14=17×3.14=53.38cm と求められる
練習問題(23年度中に補充予定)
直角三角形の転がり移動
角度が分からないから無理か…？
正三角形の転がり移動
爽茶直線上の転がり
まず単純な直線状を転がる、こんな問題から
X-1:直線上を転がる正三角形
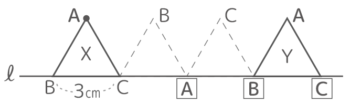
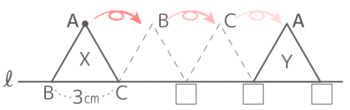右図のような1辺3cmの正三角形ABCをXの位置からYの位置まで転がすとき、以下の問いに答えなさいY[予5上8基本3′]
ヒント
長方形を転がすとき使った「あの考え方」を使いましょ
解説
長方形の転がりと同じように、どんに回転しても頂点が反時計回りにA→B→C→A→B→…と並んでいるのは変わらないことを利用する
はじめにXの状態から回転すると地面に着くのはAで、反時計回りにBがてっぺんにくるのが分かる
これを繰り返すと空欄に入るのは左から「A」「B」「C」と求められる
ヒント
(1)ができれば計算するだけ。3.14の計算はまとめて行う
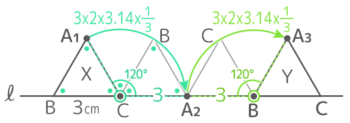
解説
(1)で決めた頂点Aの位置を結ぶと…
半径3cm中心角120°の弧が2個つながったものと分かる
よって長さは (3x2x3.14x120360)x2=4×3.14=12.56cm と求められる
練習問題(23.4.24作成中)
方形上を転がる
方形の外側
方形の外側を転がるこんな問題です
X-1:方形外を転がる正三角形
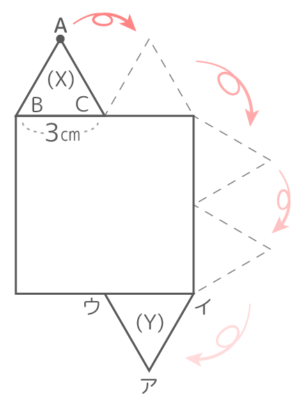図のように1辺3cmの正三角形ABCを1辺6cmの正方形の外側にそって図の(X)から(Y)まで転がすとき、以下の問いに答えよ[Y予5上8練習3(1)’]ヒント
いつものやり方で♪
解説
回転しても頂点は反時計回りにA→B→C→A→B→…と並んでいるので…
(X)の状態から回転すると地面に着くのはAで、そこから反時計回りにたどるとBがてっぺんにくるのが分かる
これを繰り返していけば(Y)の位置ではAはウにくると分かる
ヒント
正三角形の1つの内角の印をつけてみる
解説
(1)で求めた点Aを弧で結ぶと下図のようになり
これは半径3cm中心角120°の弧2個と中心角210°の弧1個の合計なので、半径3cm中心角(120×2+210)=450°の弧と等しくなる
よって長さは 3x2x3.14x450360=3x2x3.14x54=7.5×3.14=23.55cm と求められる
練習問題(23.4.24作成中)
方形の内側
長方形の内側を転がる場合、狭いスペースで軌跡がゴチャゴチャになるので丁寧に描く
X-1:方形内を転がる正三角形
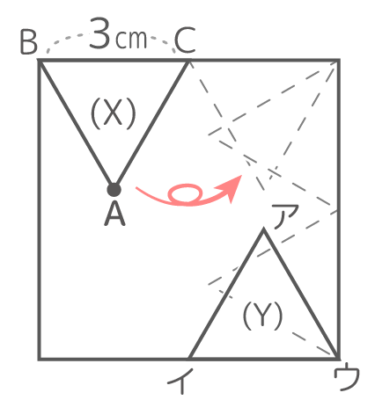図のように1辺6cmの正三角形ABCを1辺18cmの正方形の外側にそって図のXからYまで転がすとき、以下の問いに答えよ[Y予5上8練習3(2)’]ヒント
とにかく移動した三角形を丁寧に描くこと
解説
いつものように着地する点から反時計回りに点を決めていく
最初の転がりで着地するのはAで反時計回りに決めたCが次の転がりで着地して…と点を決めていくと
Aはイにあると分かる
ヒント
(1)にAが動いた跡を書いて弧の中心角を求める
解説
点Aが動いた跡(軌跡)は図のようになり
これは半径3cm中心角120°の弧2個と中心角30°の弧1個の合計なので、半径3cm中心角(120×2+30)=270°の個の長さと等しい
よって長さは 3x2x3.14x270360=3x2x3.14x34=4.5×3.14=14.13cm と求められる
練習問題(23.4.24作成中)
三角形の外側を転がる
正三角形が自分よりも大きな正三角形の周りを転がる、こんな問題
X-1:正三角形外を転がる正三角形
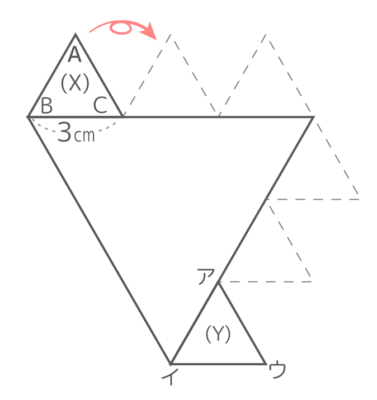1辺3cmの正三角形が1辺9cmの大きな正三角形の周りをXから一周するとき、次の問いに答えなさいヒント
(ここにヒントが入ります)
解説
反時計回りの頂点の順番を思い出して
アと分かる
ヒント
正三角形の内角(60°)に印をつけて数えると良い
解説
移動した三角形を書きAを記入して弧で結ぶと60°の弧が18個あると分かり、これは中心角(60×18)°の弧の長さと等しい(60×18は後で約分できるので計算しないでおく)
(図)
よってAが動いた跡の長さは (3x2x3.14x60×18360)=18×3.14=56.52cm と求められる
練習問題(2023年度中に補充予定)
六角形の外側を転がる
X-1:正六角形外を転がる正三角形
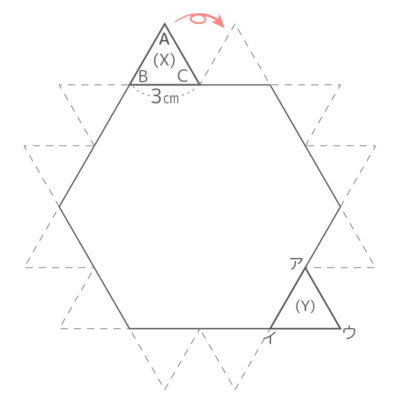1辺3cmの正三角形が1辺6cmの正六角形の周りをXから一周するとき、次の問いに答えなさいヒント
面倒臭がらずに…
解説
転がりで着地する頂点を決めたら「反時計回りの頂点順」で残りを決めて…
丁寧に繰り返すとアと分かる
ヒント
60°の印が何個あるか数える
解説
(1)で書き込んだAを弧で結ぶと弧の中心角に60°印が20個！あるのが分かり、これは半径3cm中心角(60×20)°の弧に等しい(後で約分できるので60×20は計算しないこと)
よって動いた跡の長さは 3x2x3.14x60×20360=40×3.14=125.6cm と求められる♪
練習問題(2023年度中に補充予定)
折れ線上の転がり
最後に折れ線上を転がるこんな問題を解いてみましょう
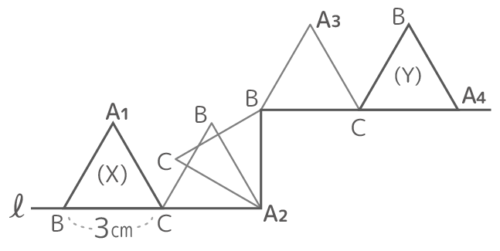
X-1:折れ線上を転がる正三角形
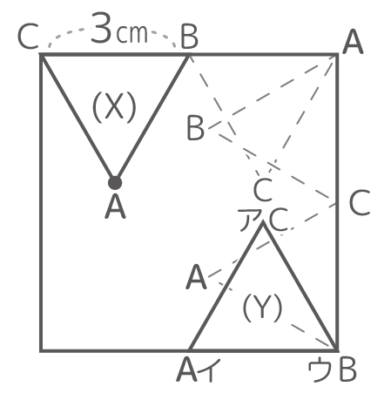
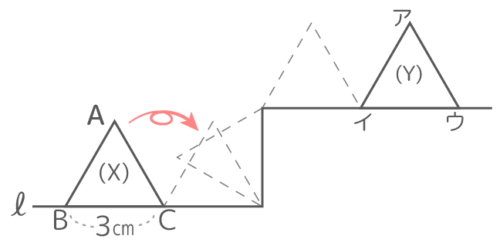図のように1辺3cmの正三角形ABCが(X)の位置から(Y)の位置まで転がるとき以下の問いに答えなさい[Y予5上8例題5′]ヒント
いつものやり方
解説
いつものコレを使って
着地した点から反時計回りに「A→B→C→A→…」と点を決めていくとこうなる
(Y)の位置で点Aはウにあると分かる。
ヒント
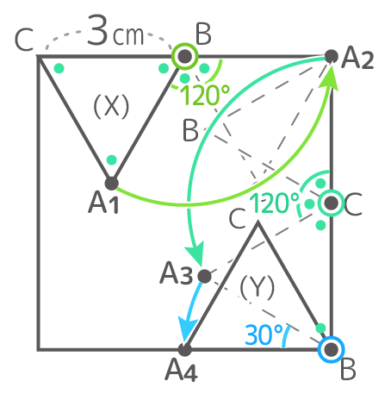
カドの内側を回るところを丁寧に書く
解説
(1)でもとめた点Aを弧で結ぶとこうなる
これは半径3cm中心角120°の弧2個と中心角210°の弧1個の合計なので、半径3cm中心角(120×2+210)=450°の弧と等しくなる
よって長さは 3x2x3.14x450360=3x2x3.14x54=7.5×3.14=23.55cm と求められる
練習問題(23.4.24作成中)
「多角形の転がり移動」は以上です。
この記事が理解できた人は続きの記事「円おうぎ形の転がり移動」に進んで下さい。
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。