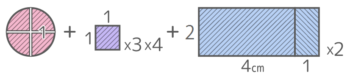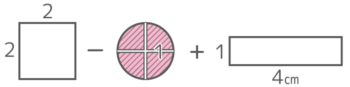
「円やおうぎ形が転がる問題」が苦手!な中学受験生の方へ
確かに「転がり移動」はイメージが難しい・計算が面倒くさいと思う人が多いです。
しかし実は計算は2種類しかなく、2種類覚えればあとは移動の様子さえイメージできれば解けてしますのです。
入試によく出る問題なので、ぜひ得意にしてほしい!
この記事では東大卒講師歴20年超の図解講師「そうちゃ」が円やおうぎ形の転がり移動の様子をイメージする方法から問題の解き方まで分かりやすく解説します。
記事を読んで例題が解けるようになれば「円おうぎ形の転がり移動」が得意になっているでしょう♪
この記事は「多角形の転がり移動」の続きなので、読んでない人はまずそちらを読むと良いでしょう
目次(クリックでジャンプ)
円の転がり移動
円の場合、多角形よりもスムーズに転がります(車輪をイメージすれば分かります)
移動の特徴
なめらかな面(線)の上を転がる場合、中心は面(線)と平行に移動する。
直線上を転がる
はじめに円が平らな直線の上を転がる場合を考えましょう
X-1:線上を転がる円
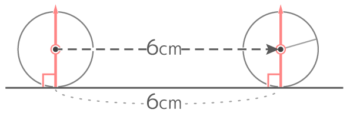
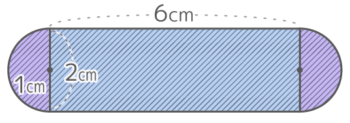
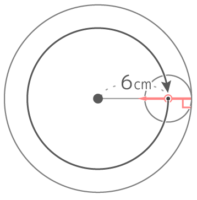
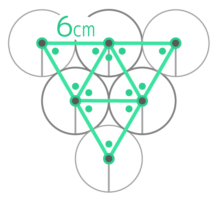
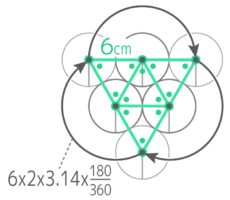
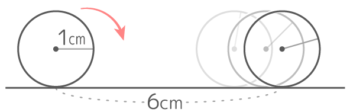 半径1cmの円が直線にそって6cm転がるとき、以下の問いに答えなさい
半径1cmの円が直線にそって6cm転がるとき、以下の問いに答えなさいY[予5上9基本1(2)’][予5上10(総合)基本9]
ヒント
中心を結びましょう
解説
ヒント
イメージできますか?
解説
分かりましたか?
曲線上を転がる
円周のようななだらかに変化する線の上を転がる場合を考える。
円の外側
まず、円の外側を転がる場合です
X-1:円の外周を転がる円
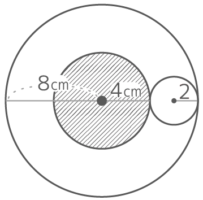
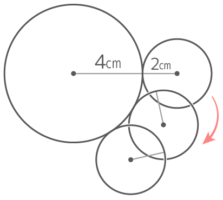 図のように半径2cmの円が半径4cmの円の外側を転がって1周するとき、以下の問いに答えなさい。
図のように半径2cmの円が半径4cmの円の外側を転がって1周するとき、以下の問いに答えなさい。Y[予5上9基本1(3)’]
ヒント
半径がいくつの円を描くか考えます
解説
ヒント
丸い形のモップで床を拭くのをイメージ
解説
分かりましたか?
円の内側
図形の内側を転がる場合は「通らない範囲」も問題になることがあります。
X-1:円の内周を転がる円
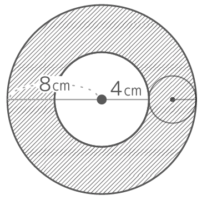
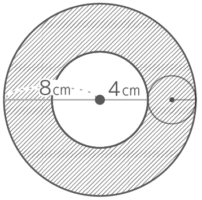
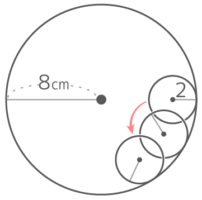 半径2cmの円Aが半径8cmの円Bの内側に沿って転がり1周するとき、以下の問いに答えなさい。
半径2cmの円Aが半径8cmの円Bの内側に沿って転がり1周するとき、以下の問いに答えなさい。Y[予5上9基本2′]
ヒント
半径が何cmになるか考える
解説
ヒント
先が丸いモップで円の内側を拭くのをイメージ
解説
円全体が動いた跡は、内側の半径(内径)4cmで外側の半径(外径)8cmの「ドーナツ形」になる
したがって、面積は (8x8x3.14)-(4x4x3.14)=(64-16)x3.14=48×3.14=150.72cm2 になる
ヒント
(2)を使ってもよいですが…
解説
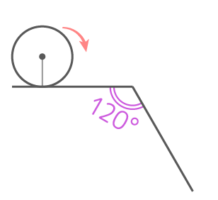
角カドの外側を転がる
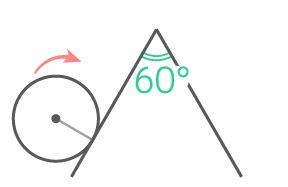
ここからは、円がなだらかに変化しない「角(カド)」がある線の上を転がる場合を考えます。
外側の曲がり方
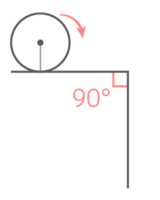
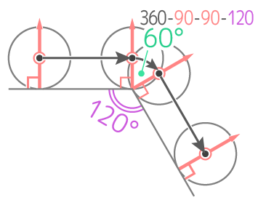
円が3cm転がって角(カド)を曲がり、さらに3cm転がって止まるとき、円の中心が通る線を作図して、角で何度回転するか求めなさい
Y[予5上9補完B][予5上9基本1(1)]
(1)90°のカド
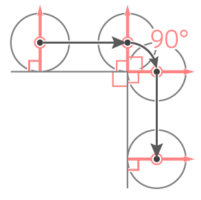
カドでは、カドと接した点を中心に単純な「回転運動」が起きる
円の中心を通り地面に垂直な線を角(カド)に2つ立て、間の角度を図る
回転する角度は360-90-90-90=90°と分かる
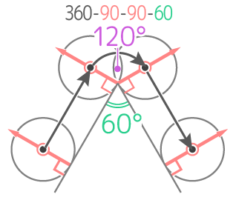
(2)60°のカド
同様に垂直な線をカドに立てて、角度を図ると…
カドで回転する角度は360-90-90-60=120°と分かる
(3)120°のカド
同様に角度を図ると
360-90-90-120=60°と分かる
カドの外側での回転の様子が分かったので、次は長さや面積を求めます。
円が3cm転がって角(カド)を曲がり、さらに3cm転がって止まるとき、円の中心が動く跡の長さを求めなさい
Y[予5上9補完B]
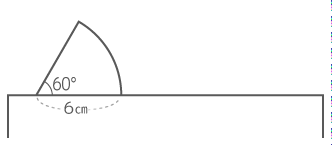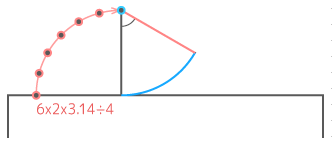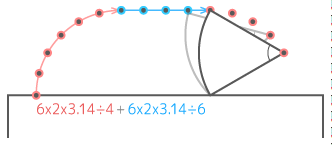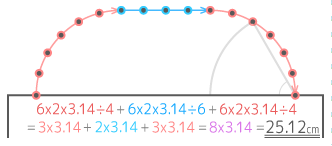
(1)90°のカド
中心が動いた跡は「直線」と「曲線」からなっている。「直線」は3cmが2つ、曲線は半径1cmの円周の90360=14になっている
したがって長さは になる。
(2)60°のカド
「直線」部分は3cmが2つ、「曲線」部分は半径1cmの円周の120360=13になっている
したがって長さは になる。
(3)120°のカド
「直線」は3cmが2つ、曲線は半径1cmの円周の60360=16になっている
したがって長さは になる。
半径3cmの円が9cm転がって角(カド)を曲がり、さらに9cm転がって止まるとき、円全部が動いた跡の面積を求めなさい
Y[予5上9補完B]
(1)90°のカド
90°のカドを曲がるとき、円全部が動いた跡は図のように、3つの部分「半径3cmの半円2つ」「横9cmx縦6cmの長方形2つ」「半径6cm中心角90°のおうぎ形」からなっている。
したがって面積は {(3x3x3.14x180360)x2}+{(9×6)x2}+(6x6x3.14x90360)=108+(18×3.14)=164.52 になる
(2)60°のカド
60°の場合は「半径3cmの半円2つ」「横9cmx縦6cmの長方形2つ」は変わらないが、真ん中のおうぎ形の中心角が120°になる
したがって面積は {(3x3x3.14x180360)x2}+{(9×6)x2}+(6x6x3.14x120360)=108+(21×3.14)=173.94 になる
(3)120°のカド
方形の外側を転がる
正方形・長方形の外側を円が転がる場合、90度のカドの外側を4回曲がる。
X-1:方形の外を転がる円
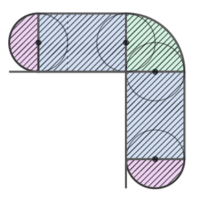
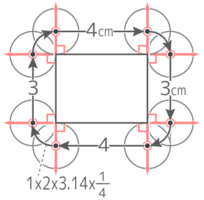
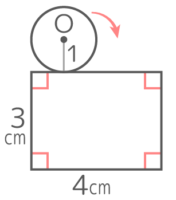 図のような長方形の回りを半径1cmの円Oが1周する時、以下の問いに答えなさい。
図のような長方形の回りを半径1cmの円Oが1周する時、以下の問いに答えなさい。Y[予5上9例題2′][予5上9基本4][予5上10(総合)基本11]
ヒント
まずカドに垂直線を立てる♪
解説
角に「円の直径と同じ長さの垂直線」を2方向に立てる(テストのときは円を描かなくてもOK♪)。
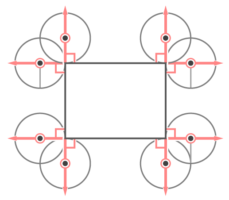
垂直線の真ん中にある中心を結ぶと円の中心が動いた跡ができる
この長さは、半径1cmの円の14の弧が4つ(つまり半径1cmの円周1つ)と、3cmと4cmの直線が2つずつ の合計なので
長さは (1x2x3.14)+{(4+3)x2}=20.28cm と分かる
ヒント
カドに立てた垂直線を使う
解説
練習問題(2023.4.17作成中)
三角形の外側
三角形の外側を転がる場合はどうなるでしょうか?
X-1:三角形の外を転がる円
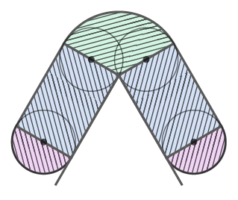
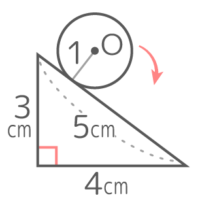 図のような直角三角形の外側を半径1cmの円が転がるとき、以下の問いに答えなさい
図のような直角三角形の外側を半径1cmの円が転がるとき、以下の問いに答えなさいY[予5上9練習3]
ヒント
まずカドに垂直線を2本立てる
解説
カドに垂直線を立てる
垂直線の真ん中を結ぶと、中心が移動した跡は「直線」と「曲線(弧)」の組み合わせと分かる
直線部分は三角形の3辺と等しいので、合計3+4+5=12cm
曲線部分は半径1cmの円の弧3つの合計で、3つの弧の中心角の合計は360°になるので、曲線部分の合計は半径1cmの円周と等しくなる
(図)
したがって長さの合計は 12+(1x2x3.14)=12+6.28=18.28cm になる
ヒント
カドにできる図形に注目
解説
三角形の形が変わっても、円全体が描く軌跡のおうぎ形の合計は円になります。
(簡単な証明)
(図)
練習問題をどうぞ(2023.4.18作成中)
おうぎ形の外側
おうぎ形の外側を転がるとどうなるでしょうか…カドの回り方に注意して下さい
X-1:おうぎ形の外を転がる円
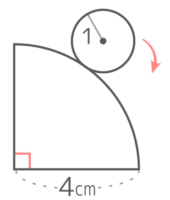 半径4cmの四半円の外側を半径1cmの円が転がって一周するとき、以下の問いに答えなさい。
半径4cmの四半円の外側を半径1cmの円が転がって一周するとき、以下の問いに答えなさい。Y[予5上9例題3′][予5上9練習2]
ヒント
まずカドに垂直線を2本立てましょう
解説
カドに円の直径と同じ長さの垂直線を2本立てる。おうぎ形のカドでは直角になる。
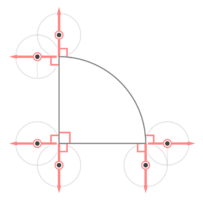
垂直線の真ん中を結ぶと円の中心が動いた跡(軌跡)ができる。
この軌跡は「直線」と半径が異なる「曲線」の組み合わせになっていて、直線部分は半径の長さ4cmが2個、曲線部分は半径1cm中心角90°の弧が3つ(つまり半径1cmの円周の34個分)と半径5cm中心角90°の弧が1つになっている。
したがって長さは (4+4)+(1x2x3.14x34)+(5x2x3.14x14)=8+{(32+52)x3.14} =8+(4×3.14)=8+12.56=20.56cm になる
ヒント
カドに立てた垂直線を使います
解説
三角形の外側を転がるのと違って、角にできるおうぎ形の中心角の合計は360°ではないので注意
(90+90+(180-中心角)=360-中心角になる)
練習問題(2023.4.18作成中)
角カドの内側を転がる
内側の曲がり方
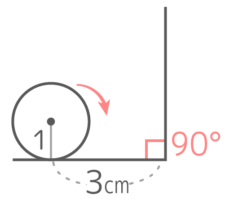 半径1cmの円が図の位置から角にくっつくまで右へ転がり、その後は同じ長さだけ上に転がるときに次の問いに答えよ
半径1cmの円が図の位置から角にくっつくまで右へ転がり、その後は同じ長さだけ上に転がるときに次の問いに答えよ
Y[予5上9補完D]
(1)中心が動いた跡の長さは何cmか
2cm動くと角にぶつかって動けなくなり、外側のときと違って回転せずに、折れ曲がる
したがって、中心が動く距離は2+2=4cmです。外側を曲がるよりも計算がラクですね。
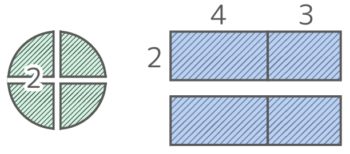
(2)円全体が動いた跡の面積は何cm2か
動いた跡を面積を求めやすいに区分すると図のようになります。
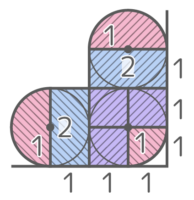
半径1cmの半円が2つ、縦2cm横1cmの長方形が2つ、一辺1cmの正方形が3つ、それとカドのところに半径1cmの四半円が1つできる。
これらを合計すると
になる。
この曲がり方の考え方を使って問題を解きます。
方形の内側
最初は正方形や長方形の内側を転がる問題を解いてみます。
X-1:方形内を転がる円
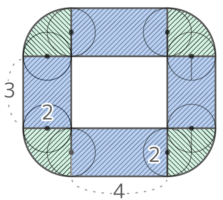
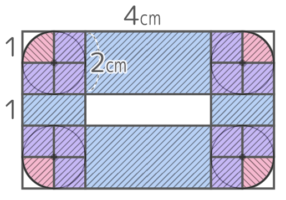
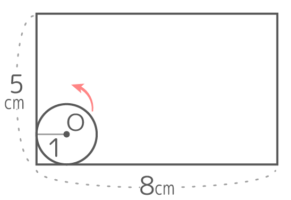 図のような長方形の内側を半径1cmの円が転がって1周するとき、以下の問いに答えなさい。
図のような長方形の内側を半径1cmの円が転がって1周するとき、以下の問いに答えなさい。Y[予5上9基本1(4)’]
ヒント
カドでの動きに注意
解説
円の動きをイメージすると…中心は角で直線的に曲がるので、中心が動いた跡は直線だけで構成される
長方形の縦横の長さから半径2個分を引いた長さだけ動いているので、その長さは (3+6)x2=18cm と求められる
ヒント
計算しやすいように分割しましょう
解説
円全体が動いた跡(軌跡)は下のようになって、計算しやすいように分割すると…
半径1cmの四半円が4個、1辺1cmの正方形が3×4=12個、幅2cm長さ4cmと長さ1cmの長方形2個ずつになる
よって面積は (1x1x3.14)+{(1×1)x3x4}+{2x(4+1)x2}=3.14+12+20=35.14cm2 と求められる。
ヒント
(2)を利用するのが簡単
解説
通った部分と通らなかった部分の形を見比べると通らなかった形の方が複雑なので、長方形の面積から(2)の答えを引いて間接的に (5×8)-35.14=40-35.14=4.86cm2 と求めるのが簡単♪
別解
分かりましたか?練習問題をどうぞ(2023.4.18作成中)
複雑な形に沿って転がる
複雑な形に沿って転がる場合、色々な曲がり方が混ざって出てきます。
折れ線
ポイントは角の外側と内側を組み合わせて作図することです。
X-1:折れ線上を転がる円
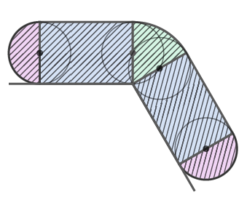
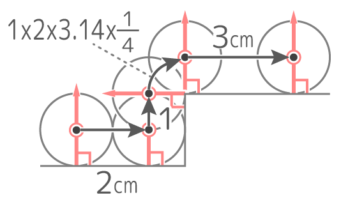
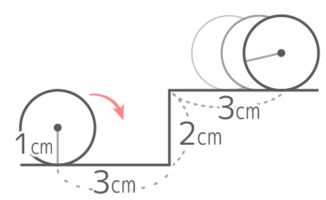 図のような段を半径1cmの円がAからBまで転がるとき、以下の問いに答えなさい。
図のような段を半径1cmの円がAからBまで転がるとき、以下の問いに答えなさい。Y[予5上9例題4′][予5上9練習6][予5上10(総合)練習6]
ヒント
外側を転がるカドには2本の「垂直線」を立てましょう
解説
スタート位置、カドにぶつかった位置、カドを曲がる位置、ゴール位置に円の直径と同じ長さの垂直線を立てる
(図)
垂直線の真ん中を結ぶと中心が動いた跡ができる。
直線部分が2cm,1cm,3cmで曲線部分は半径1cmの円の14の弧になっている。
よって長さは (2+1+3)+(1x2x3.14x14)=6+(0.5×3.14)=6+1.57=7.57cm になる。
ヒント
カドの内側を曲がる部分を上手に分割しましょう
解説
練習問題(2023.4.18作成中)
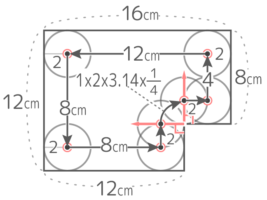
L字形の内側
長方形の一部がへこんだ「L字形」の内側を転がる問題
X-1:L形内を転がる円(作成中)
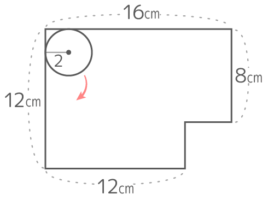 半径2cmの円が図のようなL字の内側を移動する場合、以下の問いに答えなさい。
半径2cmの円が図のようなL字の内側を移動する場合、以下の問いに答えなさい。ヒント
カドの「外」を回るか考える
解説
ヒント
区切りましょう
解説
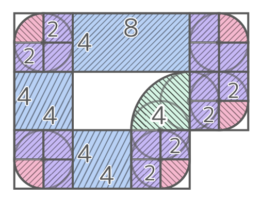
移動した跡を計算しやすいように区切る
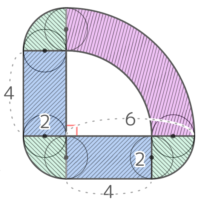
幅4cm長さ4+4+8=16cmの長方形、1辺2cmの正方形15個、半径2cmの四半円5個、半径4cmの四半円1個 の合計と分かる。
よって面積は (4×16)+(2x2x15)+(2x2x3.14x14x5)+(4x4x3.14x14)=64+60+{(5+4)x3.14}=124+(9×3.14)=124+28.26=152.26cm2 になる。
ヒント
L字形の面積から(2)を引くのが簡単
解説
L字形の面積(16×12-4×4)から(2)を引くのが簡単
(16×12-4×4)-152.26=176-152.26=23.74cm2
(別解)直接求めてみる通らなかった部分の形を観察すると…
中央部分に「4cmx4cmの正方形」1個、半径4cmの「ブーメラン形」1個、隅に半径2cmの「ブーメラン形」が5個できている。
ブーメランだけをまとめて求めると、(1辺2cmの正方形5個+1辺4cmの正方形1個)から(半径2cmの四半円5個+半径4cmの四半円)になる
(図)
よって面積の合計は (4×4)+{(2x2x5+4×4)-(2x2x3.14x14x5+4x4x3.14x14)}=16+36-{(5+4)x3.14}=52-(9×3.14)=52-28.26=23.74になる
組み合わせ円の外側
組み合わされた複数の円の回りを同じ形の円が転がる例えばこんな問題です
X-1:双円外を転がる円
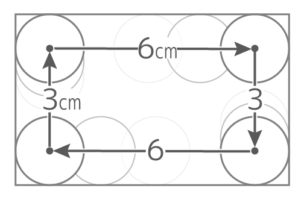
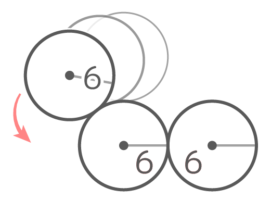 図のように接した半径6cmの円の周囲を同じく半径6cmの円が転がって一周するとき、中心が動いた跡の長さは何cmか
図のように接した半径6cmの円の周囲を同じく半径6cmの円が転がって一周するとき、中心が動いた跡の長さは何cmかY[予5上9例題5′]
ヒント
円が複数あったら、とりあえず○○を結びます
解説
分かりましたか?
もう1問、次は3つの円の周りを転がる問題をどうぞ
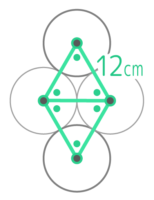
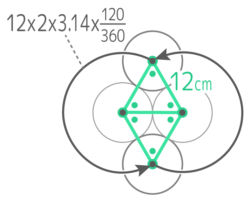
X-1:正三円外を転がる円
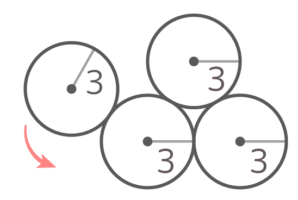 図のように接した3つの半径3cmの円の周りを同形の円が転がって一周するとき、中心が動いた跡の長さは何cmか
図のように接した3つの半径3cmの円の周りを同形の円が転がって一周するとき、中心が動いた跡の長さは何cmかヒント
接した状態を想像して円の中心を結びましょう
解説
3つの円がL字形に並んだ問題
予シリ5(上)9回[練習問題4]
L字形の3円
おうぎ形の転がり移動
平面(台)上を転がる
おうぎ形が滑らずに転がる移動
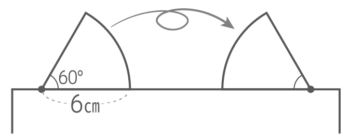
中心の動きはこうなります
なぜこんな動きになるのか?詳しく解説します。
中心の移動距離
3段階で考えると分かりやすい
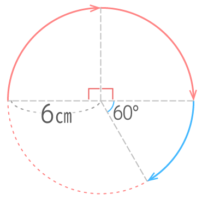
はじめに、半径が台と垂直になるまで90°回転する
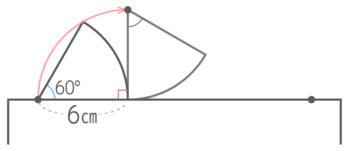
中心の移動距離は、半径6cm中心角90°のおうぎ形の弧の長さになる。
次に、もう一方の半径が台と垂直になるまで、「弧」を地面に押し付けるように転がる
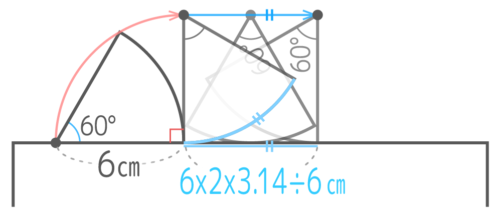
このとき、中心は地面と平行に移動する(長方形の上の辺になる)ので、地面に押し付けられた孤の長さ(長方形の下の辺)と同じ長さ(6x2x3.14x60360)になる
最後は、台にパタっと落ちて終了(90°回転。始めの動きの逆)。
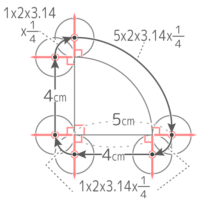
合計して、中心の移動距離は6x2x3.14x90+90+60360と考えることができる。
これを整理・計算して、6x2x3.14x150360=12×3.14x512=5×3.14=15.7cm
が答え
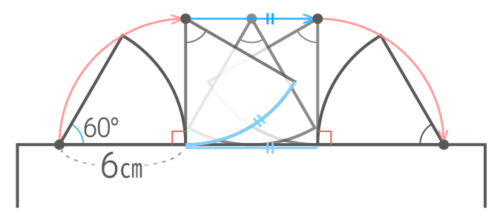
移動した跡の面積
中心の移動の様子を思い出すと

移動した面積も分かる
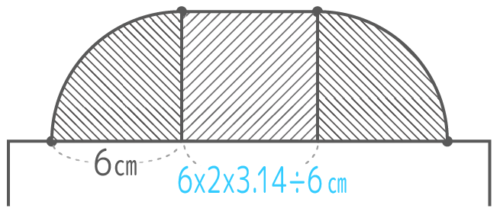
半径6cm中心角90°のおうぎ形が2つと、縦6cm、横6x2x3.14x60360の長方形が1つになる。
合計すると、(6x2x3.14x90360x2)+(6x6x2x3.14x60360)=(6×3.14)+(12×3.14)=18×3.14=56.52cm2
になる。
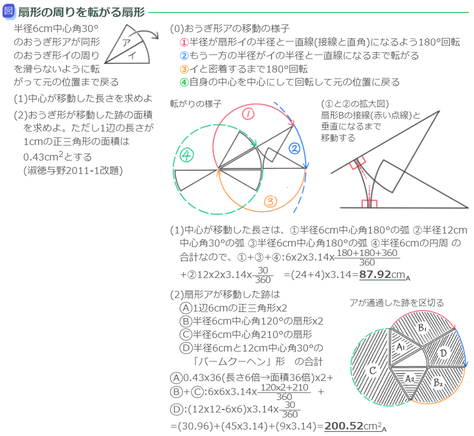
おうぎ形の周りを転がる
おうぎ形がおうぎ形の周りを転がる問題です
図解ワークをプレゼント♪パスワード「25ap25」で限定ストアに入ってお求め下さい(4/25(金)12:00まで。以降は特別割引価格になります)
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。