中学受験生で「立体図形が苦手…」という方は多いです。確かにイメージするのが難しい分野です。
でも、大丈夫ですよ!
中学受験で出題される立体図形は「柱」と「すい」の2種類だけで、覚えること(公式など)を合わせても10個くらいしか無いし、「柱」と「すい」は共通することも多いのです
だから「柱」を理解して問題が解けるようになれば立体図形の半分くらいは終了です!
この記事では東大卒講師歴20年の図解講師「そうちゃ」が柱(柱体)のイラストで分かりやすく教えます。
記事を読んで例題を解けば、円柱が好きになっているかもしれませんよ?!
目次(クリックでジャンプ)
柱体の性質
柱体の構成と名称
地面にまっすぐ立った、上の形(底面・下面)と下の形(天面・上面)が同じ立体が「柱体(ちゅうたい)、柱(はしら)」です。
算数では上の形も下の形も「底面(ていめん)」と呼ぶので、柱体には底面が2つあることになります。
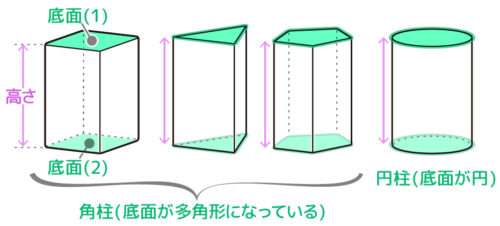
底面の形を名前にして呼びます。
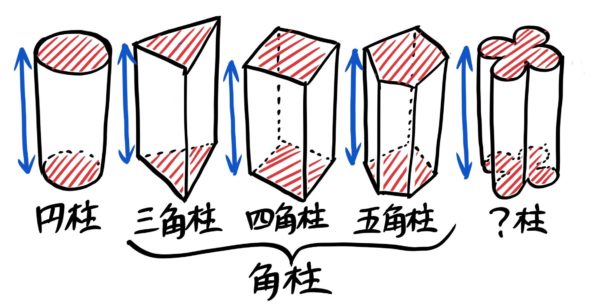
底面が円なら「円柱」
三角形なら「三角柱」
四角形なら「四角柱」
底面が多角形の場合はまとめて「角柱」とも呼びます。
そして上下の底面を垂直に測った距離が「柱の高さ」になります。
●等しい「底面」を上下に2つ持つ立体
●2つの底面の距離が柱体の「高さ」
●底面の形で分類する
底面以外の、周りをぐるっと囲む面を「側面そくめん」と呼びます。
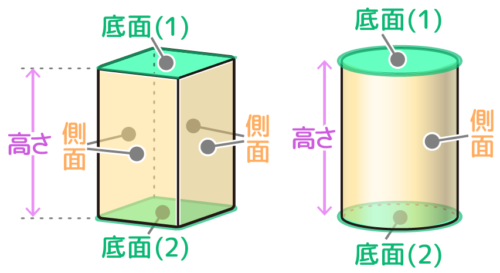
角柱はいくつかの側面を持つ
角柱は底面が多角形なので頂点・角・辺を持っています。
三角柱の場合
頂点は6個(底面の3個×2)
辺は9本(底面の3本×2+側面の3本)
面は5面(底面2つ+側面3つ)
になります。
((図))
六角柱の頂点、辺、面の数は?
→( 頂点は12個(底面の6個×2)、辺は18本(底面の6本×2+側面の6本)、面は8面(底面2+側面6) )
柱体の体積
以前に「直方体の体積=たて×横×高さ」と学習しました(参考記事「立方体直方体のまとめ」)
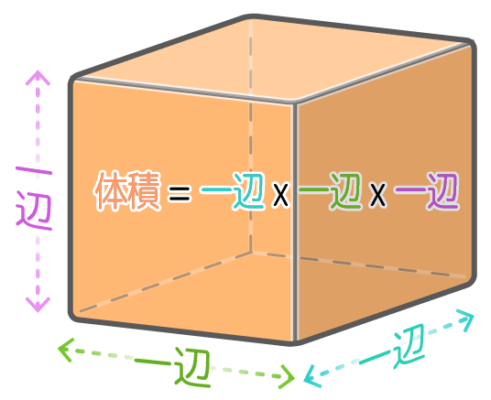
●直方体の体積=(たて×横×高さ) cm3
●立方体の体積=(一辺×一辺×一辺) cm3

この「たて×横」は底面積と同じなので「直方体の体積=たて×横×高さ=底面積×高さ」とも言えますね。
(方体=四角柱の公式図)
この理屈は底面の形が代わっても同じなので、全ての柱について「体積=底面積×高さ」が成り立ちます。
(底面積と高さだけにした柱群の図)
=底面積×高さ
柱体の展開図
●柱体の展開図は底面2つと側面1つ
●側面の幅=底面の周長
底面2つをはずし、側面を開いてひと続きの長方形にする展開図が基本です。(展開図は何種類も可能ですが、この形が一番扱いやすい)
この時、底面の周りの長さと側面の横の長さが等しくなることに注意して下さい。
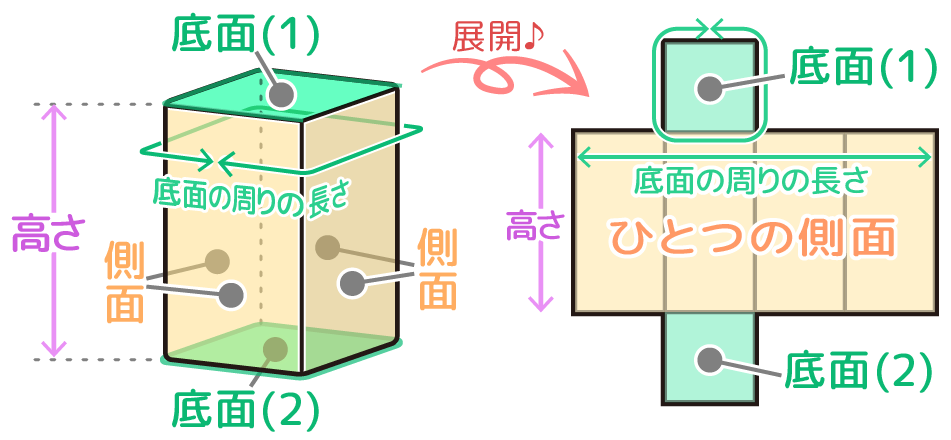
1つの長方形にすると扱いやすい
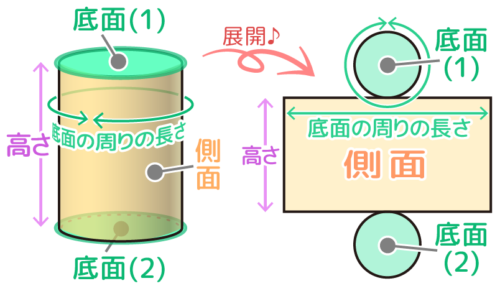
2つの底面と1つの側面ができる
確認テストをどうぞ
底面が半径1cmの円柱を展開してできる側面の縦と横の長さは?
→( 縦は円柱の高さと同じなので4cm、横は底面の円周と同じなので1×2×3.14=6.28cm )
柱の表面積
表面積は展開図の面積で、柱の展開図は「底面積」が2つと「側面積」が1つで出来ていました。
したがって「柱の表面積=底面積x2+側面積」と表すことができます。
柱の表面積=底面積x2+側面積


小まとめ
ここまでに出てきた柱の性質をまとめます
円柱の計量
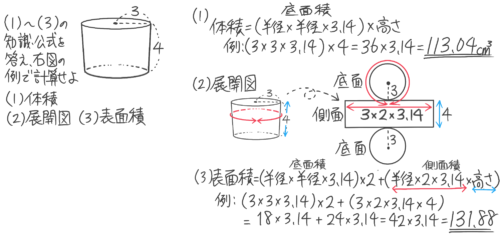
●円柱の体積=底面積×高さ
=(半径×半径×3.14)×高さ
○円柱の底面積=半径×半径×3.14
○円柱の側面積=側面の幅×高さ
=半径×2×3.14×高さ
●円柱の表面積=(底面積×2)+側面積
=(半径×半径×3.14×2)+(半径×2×3.14×高さ)
円柱の体積
円柱に限らず「柱の体積=底面積×高さ」でした。
円柱の場合は、底面積が「半径×半径×3.14」なので、体積は「(半径×半径×3.14)×高さ」になります
円柱の表面積
円柱に限らず「柱の表面積=柱の展開図の面積=底面積×2+側面積」でした。
円柱の場合、底面積は「半径×半径×3.14」、側面はヨコ(幅)が円周と同じく「半径×2×3.14」でタテが円柱の高さの長方形なので、側面積は「(半径×2×3.14)×高さ」になる。
これを合わせて、円柱の表面積は「(半径×半径×3.14×2)+(半径×2×3.14×高さ)」になる。
3.14の計算をまとめて一回にすることが重要です。
練習問題をどうぞ
XX:円柱の計量
解説
「円柱の体積=底面積×高さ」なので
(2×2×3.14)×5=20×3.14=62.8cm3
解説
「円柱の表面積=底円の面積x2+側面積になる長方形=(半径x半径x3.14)x2+{(半径x2x3.14)x高さ}」なので
(2x2x3.14)x2+{(2x2x3.14)x5}=8×3.14+20×3.14=(8+20)x3.14=28×3.14=87.92cm3
最後は3.14のかけ算一発で終わります。分かりましたか?
角柱の計量
角柱の体積
角柱の表面積
横転角柱
このような立体を考えます。
地面に接している面(底面)と反対側の面の形が違うので柱ではないように思えますが、
横に見えている面を底面と見ると、横に倒れた柱と考えることが出来ます。
柱体の加工体
円柱の縦割り
こういう立体です。
体積
表面積
柱体の複合体
柱体のくり抜き
柱の斜め切断
その他の問題
次のステップへ
最後まで読んでいただきありがとうございました!この記事があなたの役に立てたなら嬉しいです♪
次のステップへ
 爽茶
爽茶オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。