中学受験生の小5・小6で「速さと比」が苦手というのはあなただけではありません。
「速さと比」は受験算数の中でも一番難しい分野なので苦手なのもしょうがない！
ただ「速さと比」を使った問題はよく出題されるので、入試までには使えるようになっておいた方が良いのも確かです…
ただでさえ難しい「速さと比」なので、自分のペースで一つ一つ身につけていきましょう。
この記事では「速さと比」の基本になる「1人の直線上の速さと比」について東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。
記事を読んで真似すれば「速さと比」への苦手意識は消えて、次のステップへ進みたくなるでしょう♪
目次をクリックして好きな場所にジャンプできます。
前提事項
「速さと比」の前提として「速さ」と「比」が分かるようにしておきましょう。
速さの復習
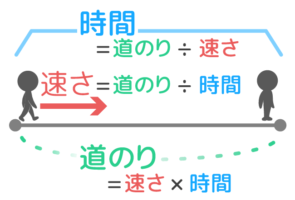
速さで使う公式はこれだけ。
➀：道のり＝速さ×時間
➁：速さ＝道のり÷時間
➂：時間＝道のり÷速さ
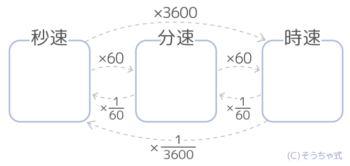
単位の変更が必要になることがあります。
◆単位時間を大きくする(→)と速さは60倍
◇単位時間を小さくする(←)と速さは160倍
詳しくは「速さの基本」を見て下さい。
比の復習
詳しくは、姉妹サイト「そうちゃ式 新1号館」の「比の基本」を見て下さい。
「速さと比」の意味
速さでは「速さ」「時間」「道のり」の3つの数値が出てきます。
このうち1つを固定すると、のこりの2つが比例(比が同じ)または反比例(逆比)の関係になります。
例えば、「速さ」が等しいとすると残りの「時間」と「道のり」は比例の関係になります。
こういうパターンが3つ(速さを固定、時間を固定、道のりを固定)あります。まずこれらを全部「言える」ように練習します。
この3つのパターンを順に見ていきましょう
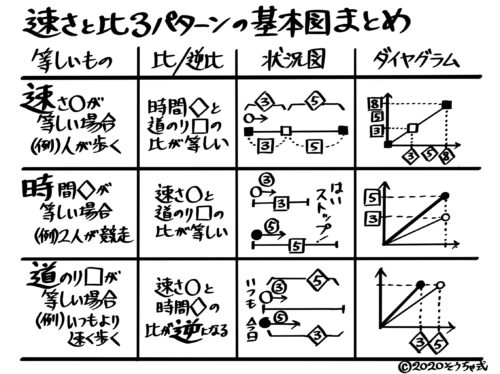
3つのパターン
速さが一定の場合
「速さが等しい」→「時間と道のりの比が等しい」
これは、誰かが一定の速さが歩いているような場合で「長い時間歩けば歩くほど進む距離も長くなる」ことを表現しています(当たり前の話ですね)。
例題1
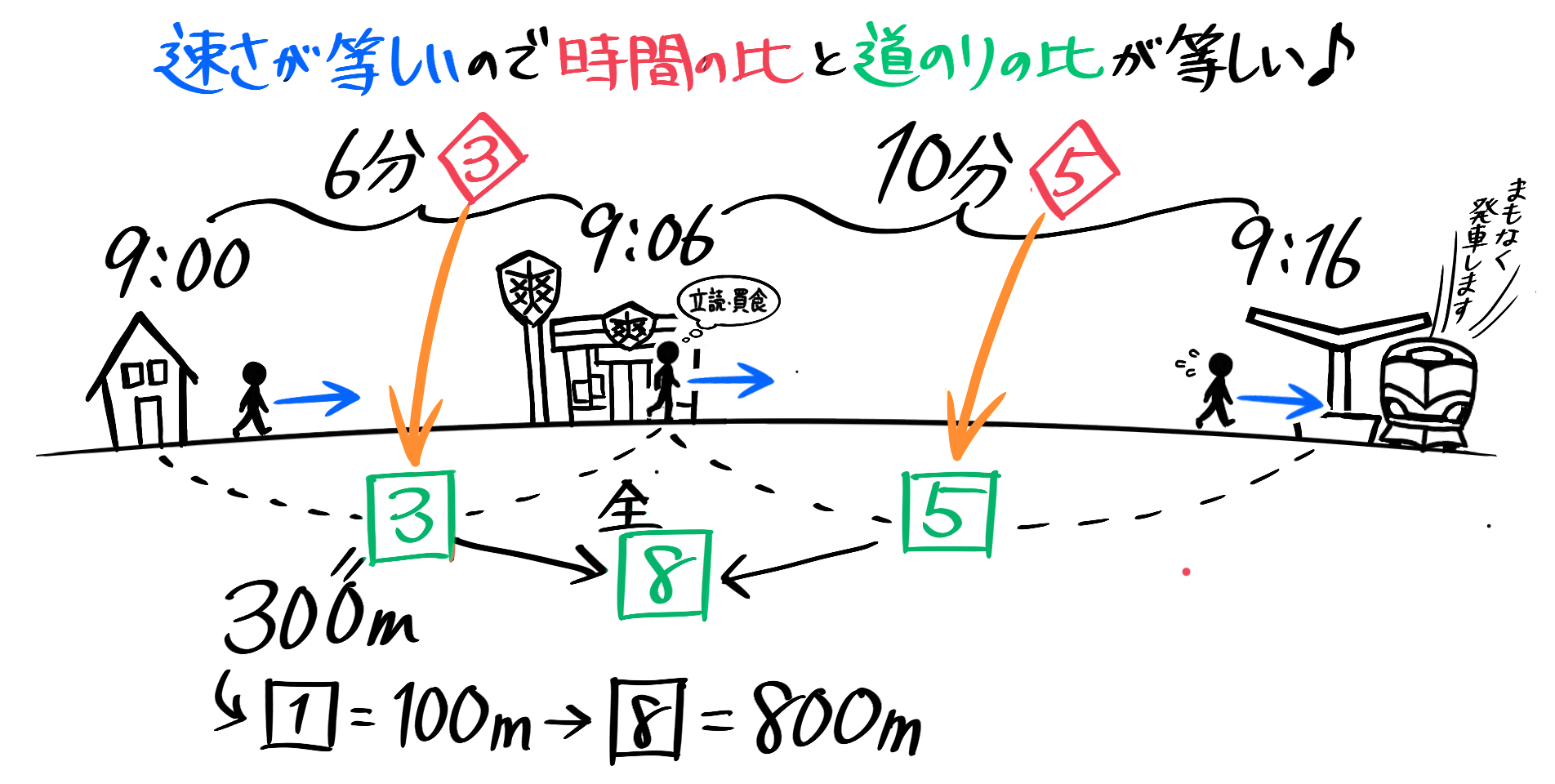
9時に自宅を出発した人が9時6分に300m先のコンビニの前を通り過ぎ、9時16分に駅に着いた。ずっと同じ速さで歩いたとすると、家から駅までは何ｍか？
簡単な状況図を描きます。私が絵が好きなのでゴチャゴチャ描いていますが、実際には「家」「コ」「駅」で十分です(汗)
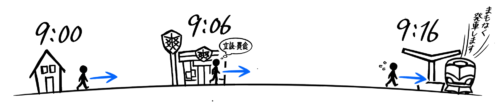
家からコンビニまで6分、コンビニから駅までは10分なので「家からコンビニまで」と「コンビニから駅まで」の時間の比は6:10=3:5になります。
そして「同じ速さで歩いた」=速さが等しいので、距離の比も時間の比と等しい3:5になります。
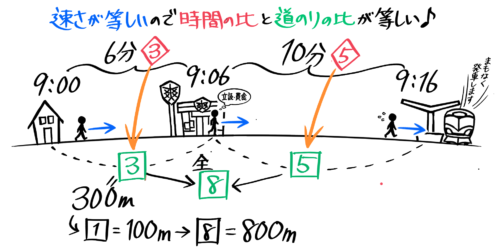
家からコンビニ(3)が300mの時なので(1)=100m、家から駅まで(8)=100×8=800mと分かります。
確認テスト
時間が一定の場合
「時間が等しい」→「速さと道のりの比が等しい」
これは、速さが異なる2人の人がヨーイドンで走りはじめストップで止まる(あるいは二人の様子を写真を取る)場合で「速い人ほど進む距離も長くなる」ことを表現しています(当たり前ですね)。
例えば、スタートラインからAは分速300mでBは分速500mで同時に走りだして何秒後かに「ストップ！」の声で立ち止まったり、写真を撮影した場合です。
2人の速さの比は300:500=3:5なので、2人が進んだ距離の比も3:5になります。
Aが立ち止まったのがスタートから40m地点の時、Bの距離を？mとすると、?:40=3:5なので ？=40×3÷5=24m地点と分かります。
確認テスト
道のりが一定の場合
「道のりが等しい」→「速さと時間の比が逆になる」
これは、速さが違う2人が同じ道のりを進むような場合で「速ければ速いほど、かかる時間は短くなる」ことを表現しています(当然ですね)。
このパターンだけ関係が逆転する(逆比になる)ことに注意して下さい。
例えば、家から学校へ普段は分速60mで行っている人が今日は分速100mで行った場合です。
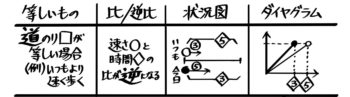
普段と今日で速さの比は60:100=3:5なので、かかる時間は逆比で5:3になります。
普段学校まで6分かかっていた場合、今日の時間を？分とすると 6:?=5:3 になるので、？=3×6÷5=3と3/5分=3分36秒 と分かります。
確認テスト
速さと比のダイヤグラム
ダイヤグラムの復習
→行動をグラフにしたもの
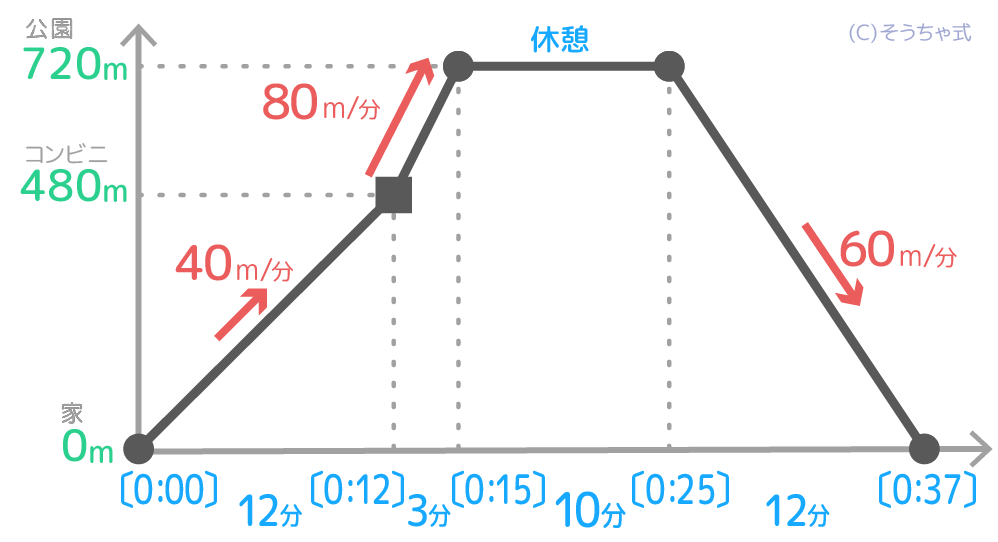
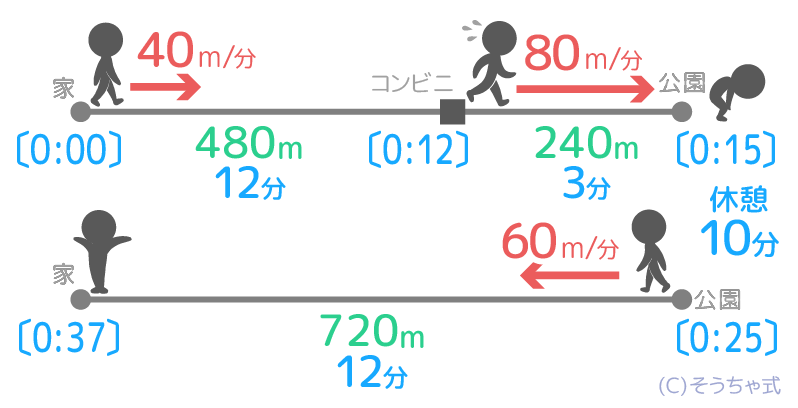
●グラフの縦軸は道のり、横軸は時間を表す
●右上がりは出発地から遠ざかる動きを、
右下がりは出発地に戻る動きを表す。
●急な坂は速度が大きいことを、
ゆるい坂は速度が小さいことを表す。
平らな部分は止まっていることを表す
◆速さはグラフ上に表れないので、
2点の時間差・距離差を使って計算で求める
詳しくは「速さの基本」内「ダイヤグラム」を見て下さい。
速さが一定の場合
➊「速さが等しい」→「一本のダイヤグラムを横軸の時間の比が3:5になるように区切ると縦軸の道のりも3:5になる」
これは相似の性質と同じです(「富士山型」相似のパターンが見えますか？)
時間が一定の場合
➋「時間が等しい」→「同じ横幅の2本のダイヤグラムの縦幅が3:5になる」
ここにも富士山型の相似ができていて、速い方の人がゴールしたときの遅い方の人の位置を相似の問題で出せます。
道のりが一定の場合
➌「道のりが等しい」→「同じ縦幅の2本のダイヤグラムの横幅が3:5になる」
比を使った速さの問題
速さの乗除
平均の速さ
速さのつるかめ算
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。