「円やおうぎ形が苦手!」という方から「応用問題が解けるようになりたい」という中学受験生の方へ
この記事では東大卒講師歴20年の図解講師「そうちゃ」が円・おうぎ形の基本から応用問題まで図を使って分かりやすく説明します。
記事を読んで真似すれば、円やおうぎ形の問題が得意になっていくでしょう♪
目次をクリックして好きな箇所にジャンプして下さい
目次(クリックでジャンプ)
円の構成
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
まず円という図形が何なのか見てみましょ♪円の意味
円は、ある一点(=「中心」)から等しい点の集合です。
円のパーツ(部品)
円で名前がついているパーツ
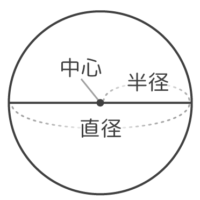
中心を通り、円を横切る直線を「直径」、その半分(中心から円まで引いた直線)を「半径」と言う。
つまり「直径=半径x2」になります
この性質を使った問題を解いてみましょう
直径と半径の問題
例題1
図のようにOを中心とする半径7㎝の円とPを中心とする半径5㎝の円がある。ABとOPの長さは何㎝か

問題文から与えられた条件を図に書き込んでから考えます。直径は半径の2倍です

AB=AC-BC=14-10=4cm、OP=OC-PC=2cmです
(図)
例題2
大中小3つの円が図のように重なっている。大円の半径が14cm、中円の半径が10cmの時、小円の半径は何cmか

小円の直径=大円の直径-中円の直径=28-20=8なので、小円の半径=8÷2=4㎝
円と角度
円の中や外に線を引いて作った角度に関する問題
((円周角の図))
円内の三角形
例題1(一つの三角形)

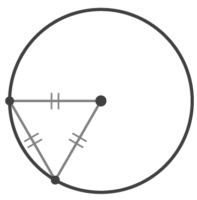
このように、円の中にあって2辺が半径である三角形は二等辺三角形になるので、必ず印をつけましょう。
((印をつけた図))
さらに頂角が60°の場合は正三角形になる
例題2(2つの明示三角形)
図の角度xを求めなさい
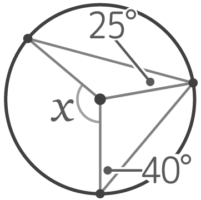
二等辺三角形の印をつけて、計算できる角度をすべて書き込むと
(図)
x=130°と分かります
(図)
例題3(2つの暗示三角形)
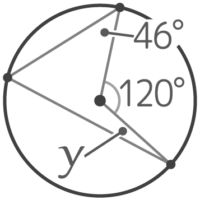
中心から半径をもう一本引くと、2つの二等辺三角形ができます。
((図))
下の二等辺三角形の頂角が152°と分かるので、y=(180-152)÷2=14°と計算できます。
((図))
このように、行き詰まったら、自分で「半径を2本使う二等辺三角形」を作ってみると良いでしょう
例題4(はみ出るタイプ(法政大中改題))
三角定規を利用する
三角定規を利用すると、書いていない長さを求めることができる。→関連記事「三角形」内「三角定規」
例題
底角が15°の二等辺三角形(Aとする)の面積を求める。
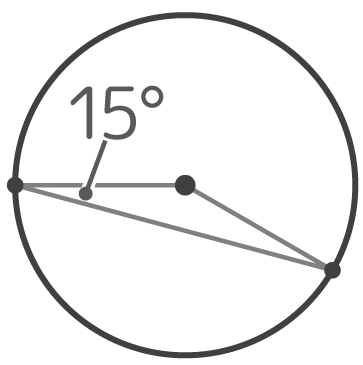
まず半径の一つを延長して直径にする
((図))→((図))
外角の性質から15+15=30°が出来るので、ここに30°60°の三角定規(Bとする)を当てると、Aの高さが半径の半分と分かる!
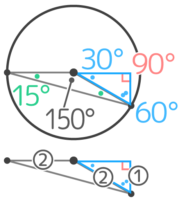
これでAの面積を求められます。
直径を使う三角形
直径を一辺とする三角形は必ず直角三角形になる。
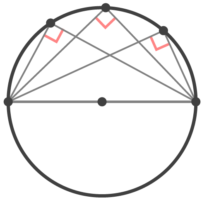
90°になる♪
(簡単な証明)
例題
円周上を動く3つの点が作る角度の問題で、この知識が使えます。
(図)
円周を等分する点
中心角
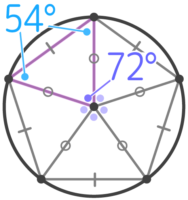
円周を等分する点から中心へ線を引くと、中心の角度も等分される
例えば、円周を5等分する点の場合、中心の角度は360÷5=72°になる
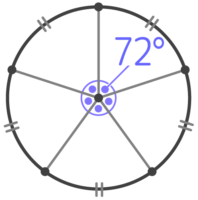
等分する点を結ぶと、二等辺三角形が5個できる。この二等辺三角形は頂角が72°なので、底角は(180-72)÷2=54°になります
例題()
正多角形の問題
この等分点を結んだ線だけを残すと正多角形になる
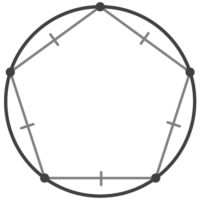
この場合は正五角形になります。
→関連記事「多角形の問題」
円の計量
円の面積や長さの問題
円周(まわりの長さ)
円周率
直径の長さを何倍したら円周の長さになるかを円周率と呼び、本来は3.1415926535…と終わりが見つかっていない(!)中途半端な小数です。
ただ、それでは計算ができないので、入試では概数(およその数)として指定されます。3.14と指定されるのが普通が、3と指定されることもあるので注意して下さい。
円周率を3.14にした場合、円周は直径の3.14倍の長さになるので、例えば、直径6cmの円の円周の長さは、6×3.14=18.84cmになります
((図))
ただ、計算する時は「直径」ではなく「半径」を使うことがほとんどなので、円周の公式も「直径」を「半径×2」に直した形「円周=半径×2×3.14」でおぼえておくのを勧めます
●円の周りの長さ=直径x円周率
(円周率を3.14としたとき、円周長=直径 x 3.14)
●「直径=半径x2」と合わせて
円周=半径 x 2 x 3.14
(例)半径3cmの円の円周の長さ
3×2×3.14=18.84cm
練習問題
円の面積
円の面積は「半径×半径×3.14」で求めることができる。
例えば、半径3㎝の円なら、3x3x3.14=9×3.14=28.26cm2 になる。(単位はcm2 (平方センチメートル))
公式になる理由
興味がある人はどうぞ
ピザを分けるように半径で円を細かく分け、上半分と下半分をそれぞれ開いて、かみ合わせるように組み合わせる
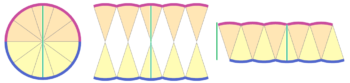
すこしデコボコしているが、平行四辺形のような形になる。(底辺は円周の半分で、高さは半径)
さらに細かく分けて同じように変形すると
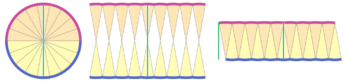
デコボコ感が消え、タテの長さが半径でヨコの長さが円周の半分の長方形に近づいている
これを繰り返すと、タテの長さが半径でヨコの長さが円周の半分の長方形になり、その面積は「半径x円周の半分」になる。

円周は直径x3.14=半径x2x3.14なので、円周の半分は(半径x3.14)になるから「半径x円周の半分」=半径x(半径x3.14)=半径×半径×3.14が面積になる♪
円の公式をまとめると、こうなります。
●円周の長さ=半径×2×3.14
●円の面積=半径×半径×3.14
(例)半径3㎝の円
(図)
円周長=3x2x3.14=6×3.14=18.84cm
面積=3x3x3.14=9×3.14=28.26cm2
円の計量の問題
例題1(公式の練習)
例題2(面積から半径の逆算)
例題3(周長から半径の逆算)
おうぎ形
おうぎ形の意味
成り立ち
おうぎ形は円を2本の半径で切り取ったもの。
(図)
「おうぎ(扇)」の形に似ているので「おうぎ形」です
ピザ1切れの方が馴染みがあるかも
構成と名称
((図))
⑤もとになる円(点線)
①中心
②半径
➂中心角
④弧
(図)
もとの円に占める割合
例えば中心角が90°のおうぎ形の場合、もとの円にしめる割合は14と直感的に分かりますね?
(90度のおうぎ形の図)
この「14」は一周360度を分母におうぎ形の中心角90°を分子にした「90°360°」を約分したものです。
この「中心角360°」つまり「おうぎ形が元の円にしめる割合」は非常に重要なので、代表的なものは憶えて下さい。
90°系
90の倍数の角度の割合は14の倍数になります
中心角90°→14 180°→24=12 270°→34
45°系
45の倍数の角度の割合は18の倍数になります
中心角45°→18 135°→38 225°→58
60°系
60の倍数の角度の割合は16の倍数になります
中心角60°→16 120°→26=13 240°→46=23
72°系
72の倍数の角度の割合は15の倍数になります。中途半端な角度に見えますが、結構出てきます
中心角72°→15 144°→25 216°→35
確認テスト(2022..5.16作成中)
●円を2つの半径で区切った図形
●「弧」=円周を区切った部分
●おうぎ形が元の円に占める割合
=中心角360
(例)中心角72°のおうぎ形の割合
→72360=15
おうぎ形の計量
おうぎ形は円の一部なので、公式も円のそれと途中までは同じです。
おうぎ形の弧の長さ
たとえば90°のおうぎ形の弧の長さは「元になった円」の周長の14になっていますね
(図)
この14は「おうぎ形が元の円に占める割合」なので、「おうぎ形の弧の長さ=もとの円の周長×おうぎ形の割合」という関係があるのが分かります。
この式に「円周=半径 x 2 x 3.14」を入れると、弧の長さの公式になります
「弧の長さ=半径×2×3.14×中心角360」
先程の中心角90°のおうぎ形の半径が6cmだとすると、弧の長さ=6x2x3.14x14=12×3.14÷4=3×3.14=9.42cmになります
((図))
おうぎ形のまわりの長さ
「まわりの長さ」と聞かれた場合は、半径2つ分を加えることに注意しましょう
例えば「中心角90°半径が6cmのおうぎ形」のまわりの長さは弧の長さ9.42cmに半径2つ分の6×2=12cmを加えた21.42cmが答えです。
(図)
おうぎ形の面積
90度のおうぎ形をイメージすれば、おうぎ形の面積も「元の円の面積」×おうぎ形の割合と分かりますね。
((図))
おうぎ形の面積=半径×半径×3.14×中心角360
上の2つの公式を逆算すると
おうぎ形の割合=おうぎ形の弧の長さもとになった円の周長=おうぎ形の面積もとになった円の面積
とも分かります。
おうぎ形の中心角
360°に「おうぎ形が元の円に占める割合」をかけると中心角になります。
おうぎ形の中心角=360xおうぎ形の割合=360xおうぎ形の弧の長さもとになった円の周長=360xおうぎ形の面積もとになった円の面積
●おうぎ形の弧の長さ
=半径×2×3.14×中心角360
●おうぎ形の面積
=半径×半径×3.14×中心角360
●おうぎ形の中心角
=360xおうぎ形がもとの円に占める割合
計量の練習問題
計算を工夫する
例題(半径と中心角からおうぎ形の弧長、周長、面積を出す)
割合を約分し、さらに前にある数値とも約分して、「3.14 x ●」の形にして、3.14の筆算1回だけにする
練習問題
例題(半径と面積から中心角を求める)
例題(半径と周長から中心角を求める)
弧を等分する点
中心角の利用
円とおうぎ形の基本知識と計算は以上です♪
「円とおうぎ形の応用問題」へ進んで下さい
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
