円・おうぎ形の応用問題が苦手…」という中学受験生の方へ
確かに、色々と面倒くさいですね。しかし、いくつかの工夫を覚えればだいぶラクになりますよ!
この記事では、東大卒講師歴20年の図解講師「そうちゃ」が円・おうぎ形の応用問題や三角形・四角形との組み合わせ問題の解き方を分かりやすく説明します。
記事を真似すれば、円・おうぎ形の応用問題が苦手ではなくなっているでしょう♪
この記事は非常に長いです。目次をクリックして好きな場所にジャンプして下さい
目次(クリックでジャンプ)
円とおうぎ形の応用問題
 爽茶
爽茶こんにちは!「そうちゃ」@zky_tutor(プロフィール)です。
まず、円とおうぎ形を組み合わせた問題を見ていきます。円の組み合わせ
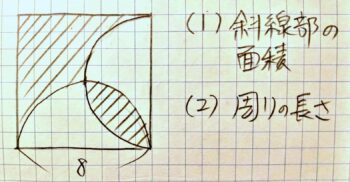
こんな形の面積や周りの長さを求めます
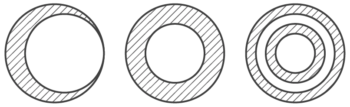
例題
計算の工夫なし
途中の計算が少し面倒くさかったと思います。面倒くさい計算というのは間違いも多くなります。
そこで計算を工夫してラクにそして正確に解いてみましょう
3.14の計算の工夫(結合法則)
3.14のかけ算が何度も出てくる場合に、それらを1つ1つ計算するのは時間がかかるしミスする可能性もある
そこで、3.14の計算を一つにまとめて、3.14の筆算は一度だけにする
例題
では、この工夫を使って、先程の問題をもう一度解いてみましょう。
随分ラクになりました♪
同心おうぎの差
中心角が同じで半径が異なるおうぎ形の差(バームクーヘン形)を求める

おうぎ形の和
多角形内部のおうぎ形の和
正三角形内のおうぎ形
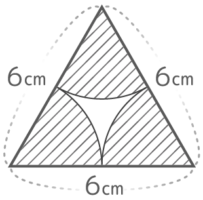
N角形の内角の和=180×(N-2)を使うと、中心角の合計が分かる
ひもの先端が動く範囲
半径が異なるおうぎ型の組み合わせ
方体のまわり
小屋につながれた(かわいそう…)動物が歩き回れる範囲
例題1
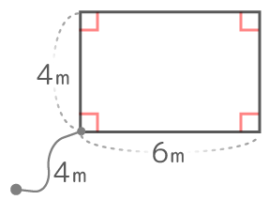
ヒモを伸ばして半径にしたおうぎ形を描くと…
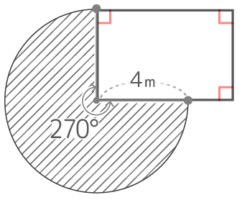
半径4㎝、中心角270°のおうぎ形になる。この面積を求めると、4x4x3.14x270360
これを約分・整理して4x4x3.14x34=12×3.14=37.68cm2になります
例題2
ひもが長くなると…
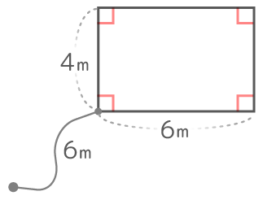
小屋の左上でヒモが折れ曲がって、半径2cm中心角90°の小さなおうぎ形ができる。
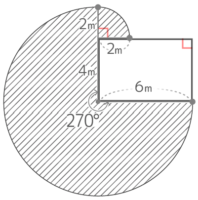
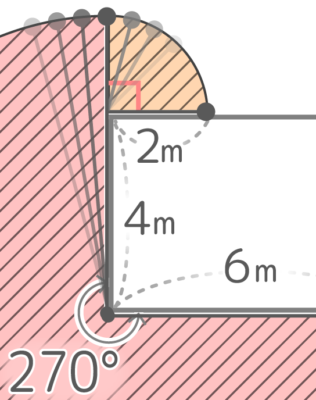
2つのおうぎ形の面積を合計して、6x6x3.14x270360
+2x2x3.14x90360
これを約分整理すると 6x6x3.14x34+2x2x3.14x14=27×3.14+1×3.14=(27+1)x3.14=28×3.14=87.92cm2です
例題3
さらにヒモが長くなると…
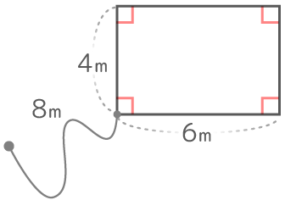
右上と左下の2箇所で折れ曲がり、おうぎ形が3種類できる
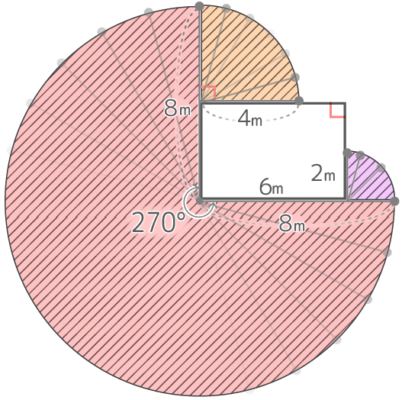
3つのおうぎ形の面積を合計して、8x8x3.14x270360+4x4x3.14x90360+2x2x3.14x90360
これを約分整理すると 8x8x3.14x34+4x4x3.14x14
+2x2x3.14x14
=48×3.14+4×3.14+1×3.14=(48+4+1)x3.14=53×3.14=166.42cm2です
その他の多角形
半円の組み合わせ(ひとだま)
パターンA
大中小3つの半円から出来る図形です。
このような図形の斜線部の面積と周りの長さを求めなさい
面積
周長
パターンB
中小の半円の半径が同じ場合、簡単な求め方があります
例題
このような図形の斜線部の面積と周りの長さを求めなさい
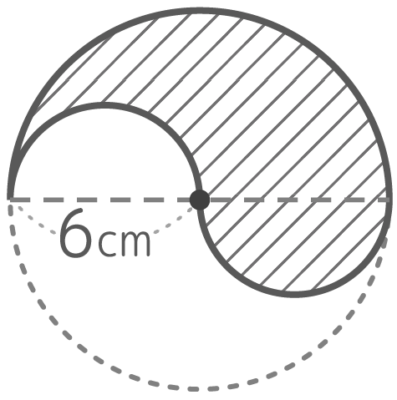
面積
部分を移して単純化
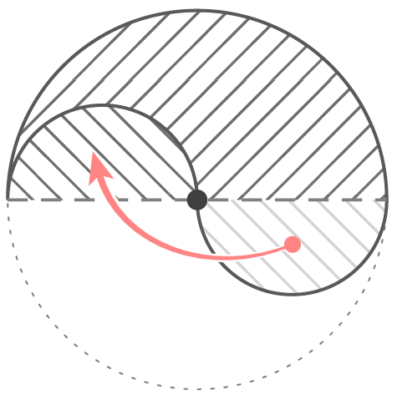
周長
四半円ー半円
円の1/4(四半円)から小さな半円を引いた形
交わる円おうぎ
次のような図形の面積と周りの長さを求めます
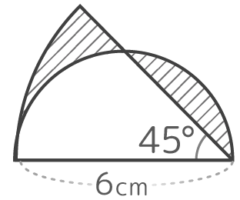
一見複雑な形のようですが、よく見ると…
面積
~部分を移し単純化
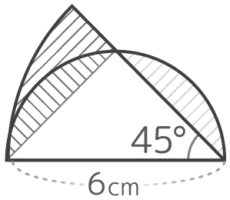
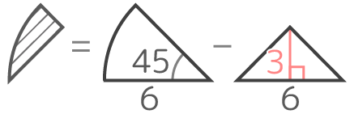
周長
~円周と弧にまとめる
円・おうぎと三角形
 爽茶
爽茶穴あきチーズ
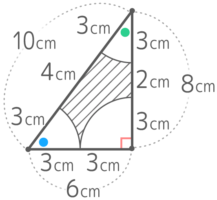
直角三角形から、頂点を中心にした半径が同じ3つのおうぎ形を除いた部分の面積と周りの長さを求めましょう
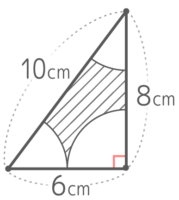
おうぎ形の中心角の和が多角形の内角の和と等しいのを利用すると、おうぎ形の中心角の和は180°と分かる
面積
周長
おうぎ形の半径が3cmなので斜線部の直線部分の長さは分かります
レンズ埋め
この図形の面積と周長を求める
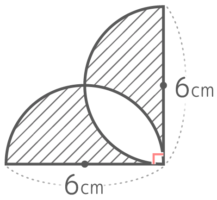
面積
右下の「レンズ」のような空白を埋めると…
底辺と高さが6cmの直角二等辺三角形になる♪
その面積は6×6÷2=18cm2です。
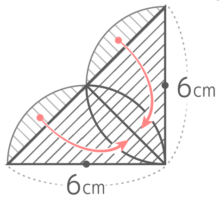
周長
斜線部分の輪郭を指でなぞると、その周長は半円の弧x2と直径6cmx2と分かります。
その合計=半径3cmの円周+12cm=(3x2x3.14)+12=18.84+12=30.84cmになります。
直角三角形の三辺を直径とする半円
半径の異なる半円3つを組み合わせた図形の斜線部と周りの長さを求める問題(「ヒポクラテスの三日月」と呼ばれる)
3:4:5の三角形
整数比になる直角三角形には「3:4:5」「5:12:13」「8:15:17」等の種類があり、一番よく出てくるのはコレ
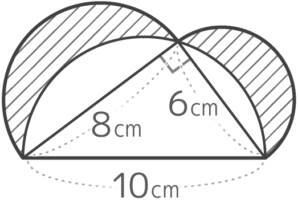
面積
斜線部の面積は「半径4㎝の半円+半径3cm半円+直角三角形」から「半径5cmの半円」を引いたものなので
(4x4x3.14x180360)+(3x3x3.14x180360)+(8x6x12)-(5x5x3.14x180360) です。
約分整理して3.14の計算は出来るだけ後回しにすると…
=(4x4x3.14x12)+(3x3x3.14x12)+(8x6x12)-(5x5x3.14x12)=(8×3.14)+(92x3.14)+24-(252x3.14)={(8+92–252)x3.14}+24={0x3.14}+24=24cm2
3.14の掛け算が0になってしまいました♪
これは、直角三角形の三辺を直径とする場合に「中半円+小半円=大半円」という関係が成り立つので、「等面積の図形の交差」問題になり、はみ出た部分の面積(この場合、斜線部と直角三角形)が等しくなるからです。
((図))
周りの長さ
周りの長さは3つの半円の弧の合計と等しいですね。斜線部のフチを指でたどると分かると思います。
3つの半円の弧の合計=(3x2x3.14÷2)+(4x2x3.14÷2)+(5x2x3.14÷2)=(3+4+5)x3.14=37.68cmになります
似た問題を解いてみましょう
その他の直角三角形
(2022.5.17作成中)
円おうぎと正三角形
例題1
2つの円が互いの中心で交わっているとき、斜線部のまわりの長さを求めましょう

中心と交点を結ぶと、正三角形ができる
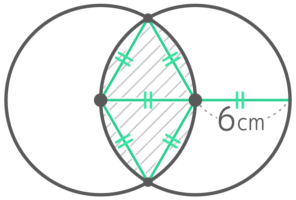
斜線部のまわりの長さは「半径6cm中心角30°のおうぎ形の弧の長さx4」と分かります
((図))
式を立てると 6x2x3.14x60360x4 、
約分整理して、 6x2x3.14x16x4=8×3.14=25.12cm です。
ちなみに、斜線部分の面積は、小学生が正三角形の面積を求めることができないので、テストには出題されないのが普通です(出題される場合「一辺が1cmの正三角形の面積は0.43cm2です」のように数値を与えられます。)
例題2
3つの円が互いの中心で交わっているとき、斜線部のまわりの長さを求めましょう
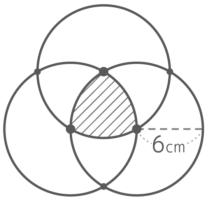
ここでも中心と交点を結ぶと正三角形ができます
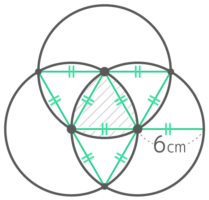
斜線部のまわりの長さは「半径6cm中心角30°のおうぎ形の弧の長さx3」と分かります
((図))
式を立てると 6x2x3.14x60360x3 で、
これを約分整理して、 6x2x3.14x16x3=6×3.14=18.84cm です。
例題3
半径6cmの円が互いの中心を通るように交わっているとき、斜線部の面積と長さを求める
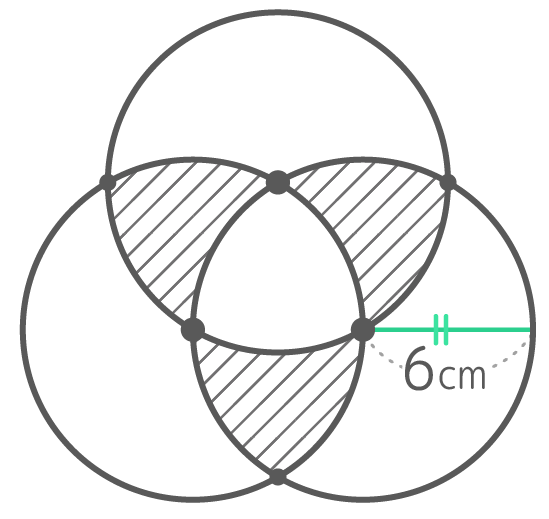
例題2と同じく、中心と交点を結ぶと正三角形ができるので、角度は分かる

周長
半径6cm中心角60°の弧が9個集まったものなので、半径6cm中心角60×9=540°のおうぎ形の弧の長さになる(中心角が360°より大きいのは変だが、あくまで計算上の話)
よって、6x2x3.14x540360=18×3.14=56.52cmになる
面積
3つの斜線部では正三角形からはみ出た部分が2つあるので、1つを正三角形からへこんだ部分へと移すと、半径6cm中心角60°のおうぎ形が3つできる。
それらを合わせた面積は半径6cm中心角60×3=180°のおうぎ形の面積に等しいので、6x6x3.14x180360=18×3.14=56.52cm2になる
円おうぎと三角定規
よく見かける、円の半径を使った15°を持つ三角形三角形AOBの面積を求める問題
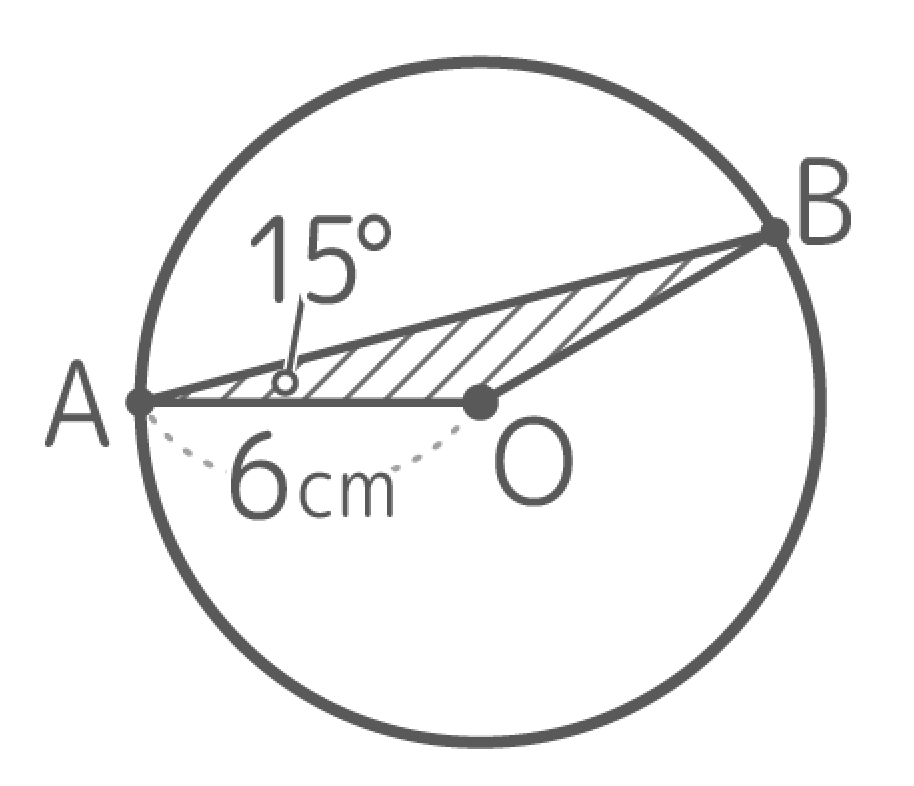
AOとOBが円の半径で等しいので△AOBは二等辺三角形で頂角(∠AOB)が150°になります。
その外角(30°)の部分に「正三角形を半分にした三角定規」を置くと、△AOBの高さが半径の半分3cmと分かる
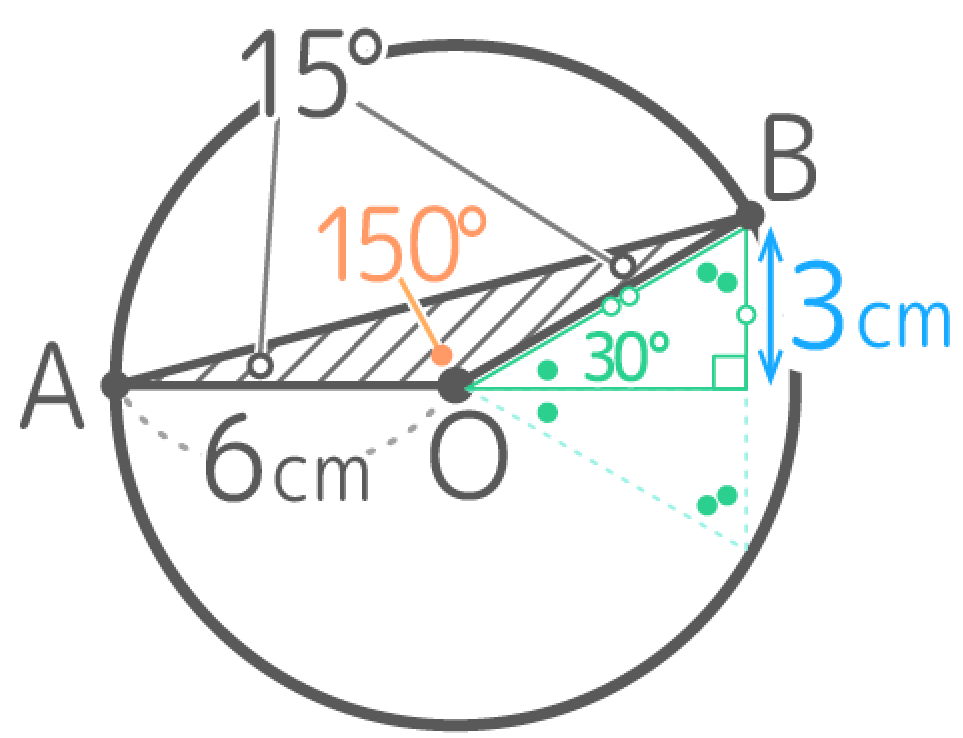
これで、面積は底辺6cmx高さ3cm÷2=9cm2と分かります。
円おうぎの折返し
正三角形が出来ます
交差する等積三角形
よく出題される問題で、「等面積の図形が交差するとき、はみ出た部分の面積が等しくなる」性質を使います
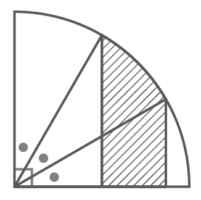
斜線部の面積を
を求める
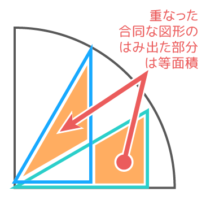
等しいので
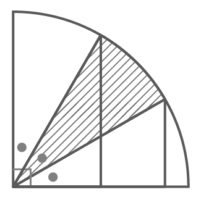
おうぎ形の
面積になる
右の扇形の面積と等しくなる
その他
変則的な分割
対称性の利用
円おうぎと方形
ここからは、円と正方形(長方形)を組み合わせた問題です
整理する問題群
一部を他の場所に移す(整理する)と単純な形にできる問題です
バームクーヘン整理
ブーメラン消し
レンズ消し
こんな図形
右下のレンズのような形を半分に割って左上の「へこみ」に移すと単純な図形になります
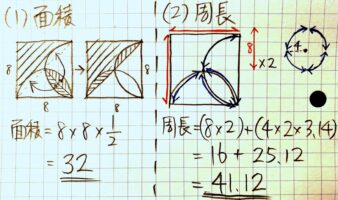
周りの長さは、同じ形の弧が4つあり合わせると円になるのを利用する
半円消し
偽レンズ消し
上で出てきたレンズ消しに似ていますが、整理できません
円おうぎと方形と正三角形
正方形の中に正三角形ができる問題

半径12cmの弧が交わると1辺12cmの正三角形ができる。
面積
正三角形の左にある細いシルエットを正三角形の右に移すと単純なおうぎ形(半径12cm中心角30°)になる
12x12x3.14x30360=12×3.14=37.68cm2
周長
曲線部分は半径12cmの四半円(90°)の弧と60°の弧の合計なので、半径12cm中心角150°のおうぎ形の弧の長さ
12x2x3.14x150360=10×3.14=31.4cm
直線部分は正三角形の1辺=12cm
これらを合計して31.4+12=43.4cm
半円+方形
方形の外に半円が付加された問題
1辺の長さが分からない方形
正方形に外接する四半円
正方内で接する2つの四半円
半径が分からない円の面積
ひし形としての正方形
正方形は長方形(4つの角の大きさが等しい=直角)とひし形(4つの辺の長さが等しい)の性質を兼ね備えているので、面積を求める公式も長方形型の「一辺(たて)×一辺(よこ)」とひし形型の「対角線×対角線÷2」の二種類が使えます。
●長方形型の公式
正方形の面積=一辺×一辺
●ひし形型の公式
正方形の面積=対角線×対角線÷2
円との融合問題を解くコツの1つ目が、この2つの式です。
円と正方形の位置関係
円との融合問題を解く2つ目のコツが、円と正方形がくっつく(接する)際の位置関係です。
正方形と円の位置は「外接」と「内接」の2種類があります。
外接(円)
正方形の角に接するように、円が正方形の外側にある場合

内接(円)
正方形の一辺に接するように、円が正方形の内側にある場合
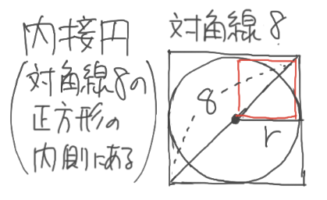
半径不明の円の面積を求める
「円の面積=半径×半径×3.14」ですが、半径が分からない円の面積を出すように求められることがあります
しかし先程の「ひし形としての正方形」と「正方形に接する円」の考え方を使うと、半径そのものは分からなくても「半径×半径」は求められるので、円の面積を求めることができます。

半径そのものは分からなくても
「半径×半径」は分かります♪
確認テスト
(2021.3.22作成中)
バナナ形
下図のような形
(バナナ図)(レンズ図)
これらは上の「外接円」から正方形を引いた形を1/4または1/2したもの。よく出てくるので面積を求めておく。
バナナ型の求め方(半径が1の場合)
((図))
バナナ型=(半径1の円の面積-正方形(対角線が2のひし形)の面積)×1/4=(1×1×3.14-2×2×1/2)×1/4=(3.14-2)×1/4=1.14×1/4=0.285 になります。
つまりバナナ型一つを正方形に入れた図にした場合、正方形の面積が1なのでバナナ型は「正方形の面積×0.285」になります。
(図)
レンズ形はバナナ形2つ分なので「正方形の面積×0.285×2=正方形の面積×0.57」になる。一部のテキストや参考書ではこの数値を暗記させるようだ。
個人的には、バナナ形を「(3.14-2)×1/4」で憶えておくのが良い気がするが…
バナナ形を作る
こんな図形の面積と周囲の長さを求めます
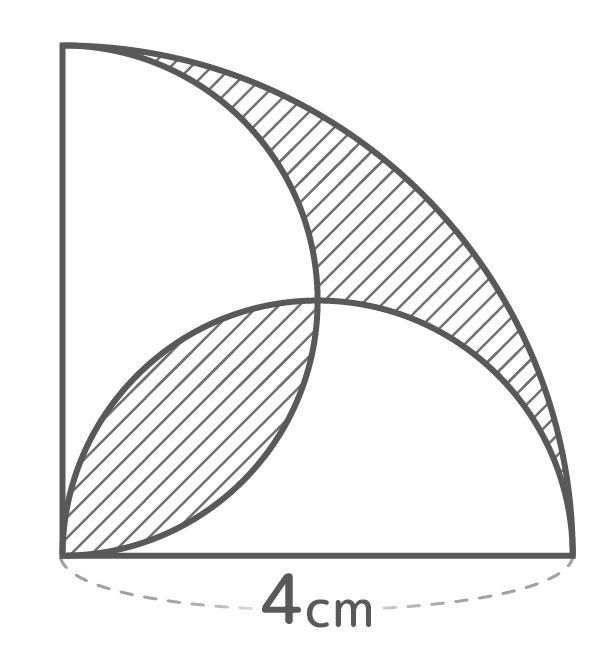
面積
左下の「レンズ」のような形を2つに分けて、右上の形の凹みに移すと単純な形(バナナ形)になります

上で出した通り、
周長
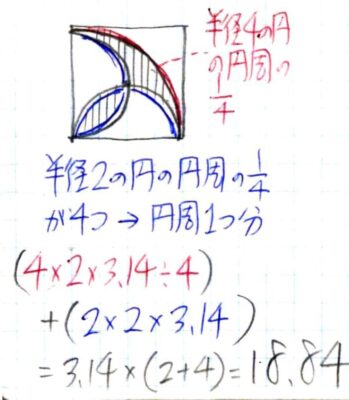
大きな円の四半周と小さな円の円周の合計と分かります
ブーメラン形
下図のような形
(図)
これは、正方形から「内接円」を引いた形を1/4したもの。
ブーメラン形の求め方(半径が1の場合)
((図))
ブーメラン形=(一辺2の正方形の面積-半径1の円の面積)×1/4=(2×2-1×1×3.14)×1/4=(4-3.14)×1/4=0.86×1/4=0.215 になります。
つまりブーメラン形一つを正方形に入れた図にした場合、正方形の面積が1なのでバナナ型は「正方形の面積×0.215」になります(正方形の面積の半分0.5からバナナ形0.285を引いたのと等しい)。
これも、忘れても復元できるように「(4-3.14)×1/4」で憶えておくのが良い気がします
●バナナ形
=(外接円-正方形(ひし形))×1/4
=(3.14-2)×1/4=正方形の面積の0.285倍
○レンズ形(バナナ×2)
=正方形の面積の0.57倍
●ブーメラン形
=(正方形-内接円)×1/4
=(4-3.14)×1/4=正方形の面積の0.215倍
計算の工夫
試しに、下の図の斜線部の面積と周りの長さを求めてみる。
面積を求める
面積を出す場合は一部の形を移動すると単純な形に出来ることが多い
周りの長さを求める
周りの長さを求める場合は、半径が違う円にまとめていき、3.14の計算を1回だけにするとミスが減る
バナナとブーメランの利用問題
を解いてみましょう
バナナ集合体
バナナ形がいくつも集まった形
レンズ
この形を憶えるとするテキストもありますね。
「そうちゃ式」ではバナナが2つ集まった形と考えます
花びら
「バナナ」が8個集まった形
バナナ十字
「バナナ」4個と等しくなる
円の重なり
2つの円が重なった部分の面積を求める場合も「バナナ」を使うことがある
ブーメラン集合体
ネガレンズ
上で見たレンズ形を白黒反転(ネガ)させた形。ブーメラン2個と等しい
ネガ花びら
上で見た花びらを白黒反転させた形。ブーメラン8個と等しい
四芒星
ツノが4つある星のような形。ブーメラン8個と等しい
二重のブーメラン
水平垂直のバナナ
円おうぎと多角形
棒を束ねる
3本の棒をヒモで束ねている断面図を想像します

この図形の角度や周囲の長さ(太線の部分)、内側の面積を求めます。
円おうぎと六角形
交わる等積の角円
四半円と三角形
四半円と四角形
双四半円
双半円
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。