「点が動く問題が苦手!」という中学受験生の方、
東大卒講師歴20年の図解講師「そうちゃ」が、三角形や四角形の辺の上を点が動く問題の解き方・コツを伝えます。
記事の真似をすれば動点の問題が苦手ではなくなるでしょう。
目次(クリックでジャンプ)
動点問題を解く準備
コチラを見て下さい
1動点が作る面積の問題
多角形の周上を動く点と多角形の頂点で作られる三角形の面積の変化を出す問題で、動点問題で一番多く出題されます。
長方形を周回
上で出したのと同じく、縦6cm横8cmの長方形ABCDの辺上をAからB→C→Dと2cm/秒で動く点Pが作る三角形ADPの面積の変化を考えます
(1)Pが出発してから2秒後の三角形ABPの面積は?
(2) 〃 4秒後の 〃 ?
(3) 〃 6秒後の 〃 ?
(4) 〃 8秒後の 〃 ?
(5)三角形ABPの面積はどのように変化するかグラフにしなさい
(6)三角形ABPの面積が20平方cmになるのは何秒後か?
準備(時刻を書く)
まず、点Pが各頂点に着く時間を書き込みます。
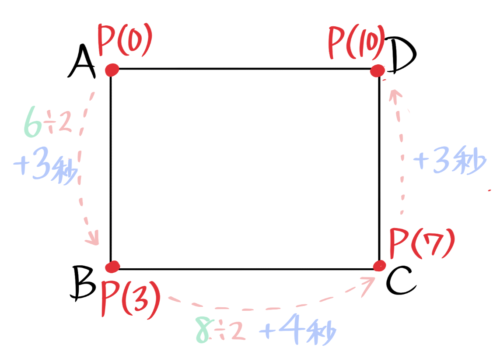
これで(1)2秒後はPはAB上にいて、(2)6秒後と(3)8秒後はBC上、(4)8秒後はCD上とイメージできます。
問われた時刻の図を書いて解く
(1)2秒後にPは2×2=4cm進んでいます。
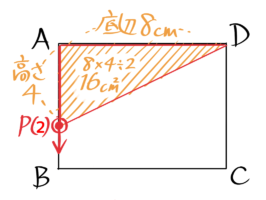
面積は16cm2になります。
(2)4秒後にPは2×4=8cm進んでいます。
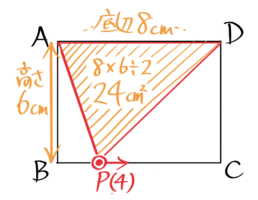
面積は24cm2になります。
(3)6秒後にPは2×6=12cm進んでいます。
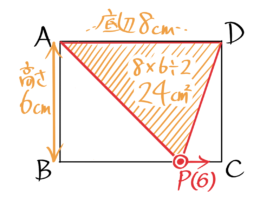
面積は24で4秒後と同じです。
つまりBC上を移動する間はADPの面積は変わらないのが分かります。
(4)6秒後にPは2×8=16cm進んでいます。
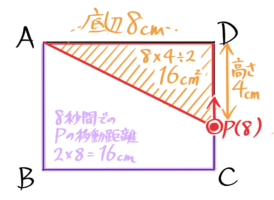
16cm進んだPの位置はCを2cm過ぎたところなので、三角形ADPの高さは4cmになるので、面積は8×4÷2=16になります。




グラフにする
(5)
Pが各頂点に着く時間を基準に3つの時期に分けて考えます。
●Pが辺AB上にある場合(0秒~3秒)
底辺AD8cmは変わらず、高さAPが大きくなるので、三角形ADPの面積はどんどん大きくなります。
0秒後の面積を求めると0cm2、3秒後の面積を求めると8×6÷2=24cm2 になります。
つまり0秒から3秒にかけて、面積は0cm2から24cm2に増加します。
●Pが辺BC上に~(3秒~7秒)
底辺AD8cmは変わらず、高さ6cmも変わらないので、三角形の形は変わりますが面積は8×6÷2=24cm2のまま変わりません。
つまり3秒から7秒にかけて、面積は24cm2のまま変わりません。
●Pが辺CD上に~(7秒~10秒)
底辺8cmは変わらず、高さが小さくなるので、三角形の面積はどんどん小さくなります。
7秒後の面積を求めると24cm2、10秒後の面積を求めると8×0÷2=0cm2になります。
つまり7秒から10秒にかけて、面積は24cm2から0へと小さくなります。。
以上の面積の変化をグラフにするとこうなります。
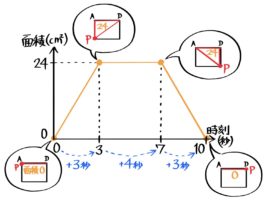
グラフが折れ曲がるポイントに
なっているのが分かる
動点が各頂点に着く時刻の三角形の面積がポイントなので、これも書きこんでしまうとよいでしょう。
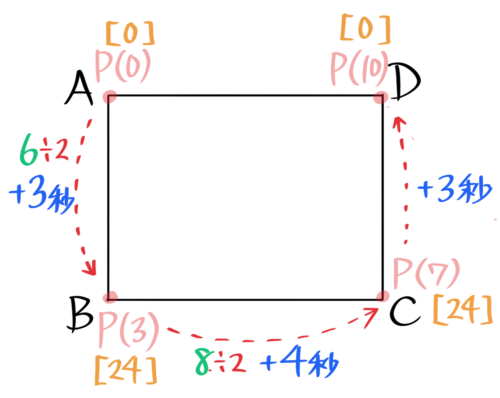
三角形ADPの面積を書き込む
面積から時刻を求める
(5)
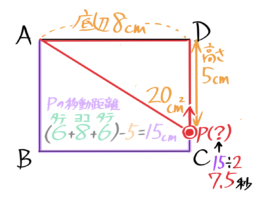
今までとは逆に面積を指定された場合です。
さっき書きこんだ面積の数値[0][24][24][0]を見れば、20cm2になるのはAB上にある場合(Bの少し手前)とCD上にある場合(Cを少し過ぎたあたり)の2回あるのがイメージできます。
その2つの三角形とその中に面積20も書き込むと、底辺は8cmなので高さは8×□÷2=20cm2を逆算して5cmと分かるのでそれも書き込みます
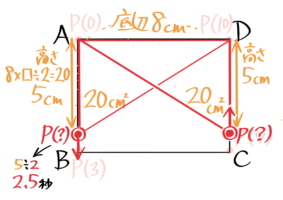
この状態になる二つの時刻を求めれば答えになります。この時はスタートのAから何cm移動した状態かを考えます。
はじめの状態はAから5cm進んでいるので5÷2=2.5秒後です。

二番目の状態はDから5cmなので、AからDまでの距離6+8+6=20cmから5cmを引いて、Aから15cm進んでいると分かります(この出し方は好きな方法で構いません)
よって二番目の状態は15÷2=7.5秒後と分かります。
確認テスト
三角形周上の動点
例えば、A= B= C= cmである三角形ABC上を2cm/秒の速さでA→B→Cと移動する点Pが作る三角形APBの面積を考えます。
台形周上の動点
台形の高さ辺を往復する点
二つの動点の旅人算
動点が二つある場合、旅人算の出会い・追い付きと同様に考えます。
出会い
追い付き
二動点を結ぶ線の問題
二つの動点を結んだ線を考える問題です。
多角形上の動点問題は以上です。
オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
