「時計算がよく分からない…」という中学受験生の方へ。
あなたは運が悪かっただけです!分かりづらいテキスト/分かりづらい授業/分かりづらい説明を最初に見た/受けたので、時計算を簡単にする考え方が理解できていないのでしょう。
時計算は「旅人算」と同じように考えれられます。むしろやることはいつも同じなので簡単かもしれません。
この記事では、東大卒講師歴20年の図解講師「そうちゃ」が時計算を旅人算と共通の考え方で分かりやすく説明します。
記事を読んで例題を解けば、時計算が好き・得意になっているでしょう♪
目次をクリックすると好きな場所にジャンプできます。
目次(クリックでジャンプ)
時計盤の「角度」
長針と短針2つの針が作る角度を考えるのが時計算の問題です。
時計盤の文字1つの角度
1周(360°)を12等分するので、360÷12=30°になっている。
○時ちょうどの両針の角度
例えば4時ちょうどの長針と短針の角度を考えると、文字1つが30°なので、30×4=120°と分かります。
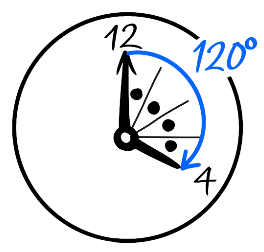
角度の答え方
また10時ちょうどの場合は30×10=300°(A)になりますが、自然な感覚としては360-300=60°(B)と感じます。
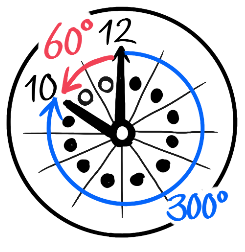
180°より大きいので、
360-300=60と答える
実際、テストでも「小さい方の角度」「180°以下の角度」と指定があるのが普通です。この場合は「60°」と答えないとバツになります。
ただ、これは答えるときだけの処理で、途中計算では360から引くことはしません(分数計算で、途中では仮分数を使って答えるときに帯分数に直すのに似ています)
小まとめ
●時計盤の角度:文字一つの角度~30°(図左)
●N時ちょうどの角度~(30xN)°
(例1)4時ちょうど→30×4=120°(図中)
(例2)10時ちょうど→30×10=300°(180より大きい)
→360°-300°=60°(180より小さい方)(図右)


長針と短針の「角度」
針の速度
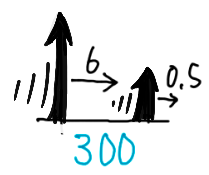
今まで速さの単位は「時/km」のように「長さ/時間」で表しましたが、長針や短針の速度は「1分で何°回転するか」=「角速度」で表します。
長針の角速度
長い針は1時間(60分)で1周(360°)するので
360÷60=6°/分(ろくど まいふん)という角速度になります。
((図))
短針の角速度
一方、短い針は1時間(60分)で文字一つ分30°しか進まないので
30÷60=0.5°/分(れいてんごど まいふん)という角速度です。
((図))
時計算は○○算に似ている
ここで、毎正時からの時計の長針と短針の動きを考えます。
たとえば4時ちょうどを例にすると、短針と長針の角度は30×4=120°なので、速さ6°/分の長針が速さ0.5°/分の短針を120°「後ろ」から、追いかける形になっています。
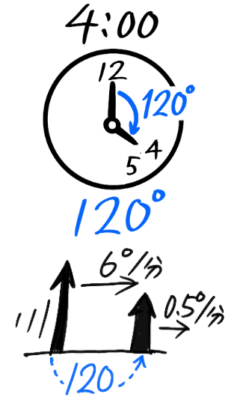
これは旅人算(追いつき)と状況が似ていますね♪
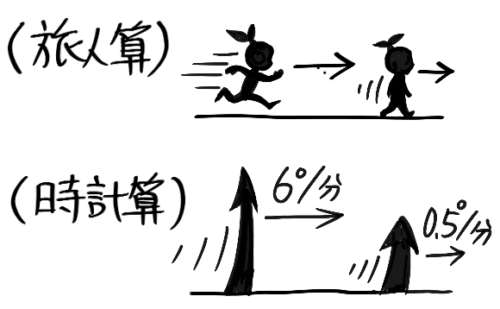
ただ、旅人算では2人の速さは問題ごとに違うのに対して時計算では長針と短針の速さ(角速度)は6°/分と0.5°/分に決まっています。
そこで「時計算」というのは旅人算(追いつき)の速さが決まったバージョンと考えます。
ここで、速さの公式と旅人算(追いつき)の公式を復習すると、こうでした。(旅人算を完全に忘れた!という人は、関連記事「旅人算まとめ」内「追いつきの旅人算」を見て下さい)
❶時間=道のり÷速さ
②道のり=速さ×時間
③速さ=道のり÷時間
❶追いつく時間=2人の距離÷速さの差
②2人の距離=速さの差×追いつく時間
③速さの差=2人の距離÷追いつく時間
「速さの差」を計算に使ったのを思い出しましたか?時計算では「速さの差」の代わりに両針の「角速度の差」を使います。
長針の角速度6°/分ー短針の角速度0.5°/分=角速度の差5.5°/分で、これは「長針は短針との角度の差を1分で5.5°縮めていく(または広げていく)」ことを意味します。
時計算の計算は、この「5.5°/分」を必ず使うので憶えましょう
→角速度(角度÷時間)で表す
●長針の速さ
→360°÷60分=6°/分(速い)
●短針の速さ
→30°÷60分=0.5°/分(遅い)
●両針の速さの差
→6-0.5=5.5°/分
→両針の角度は毎分5.5°ずつ変化していく
ここからは、「時計算=旅人算」という考え方で問題を解いていきます。
長針と短針が重なる
例えば4時から5時の間で、長針と短針が重なる時刻を出してみます。
「長針と短針が重なる」は旅人算的に「長針が短針に追いつく」と考えます
先程見たように「4時ちょうど」は角速度6°/分の長針が、30×4=120°「前」を角速度0.5で逃げる短針を追いかけ始める状態です。

追いかけ始める
ここから、旅人算の追いつく時間の公式「追いつく時間=2人の距離÷速さの差」と同じ用に考えて、
長針が短針と重なる(追いつく)時刻=両針の角度÷角速度の差
で求められます。
この場合、4時ちょうどの両針の角度は30×4=120°、角速度の差は6-0.5=5.5(こちらはいつも同じ)なので、
長針が短針に追いつく時間=120÷5.5=1205.5=(分子分母を10倍)=120055=24011=21911分と分かります。
つまり両針が重なる時刻は4時21911分です!
両針が重なる時刻
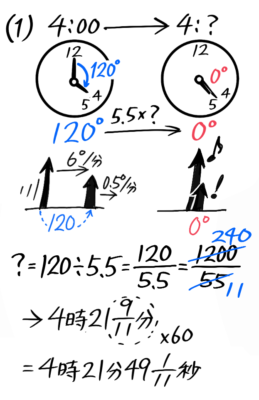
ここで、面倒くさいのですが秒まで求めてみましょう。
「1分=60秒」なので分(ふん)の分数部分911を60倍すると秒にできます。
計算すると911x60=54011=49111なので、重なる時刻は4時21分49111秒です。
分母の11は消えないのでやはりスッキリしない答えですが、まあしょうがない…
●N時から(N+1)時の間で両針が重なる時刻
→N時{(30xN)÷5.5}分
→4時ちょうどの両針の角度は30×4=120°
→ここから5.5°/分の角度が縮んで行くので
→120÷5.5=21911分
→重なるのは4時21911分=4時21分49111秒
確認テスト
10時から11時の間で長針と短針が重なる時刻は?
長針と短針が重なる時刻
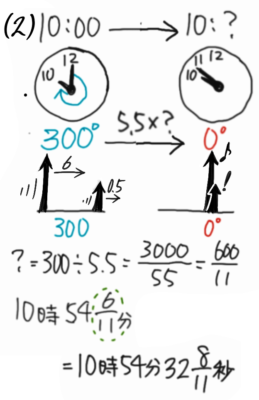
ある時刻の角度
ある時刻(N時M分としておきます)の角度を考える場合も、まずN時ちょうどの両針の角度を求めます。
例えば4時10分での両針の角度を求めるなら、まず4時ちょうどの角度を30×4=120°と求めておきます。
これは、さっき見たように、短針が長針の120°「前」にいる状態です。

追いかけ始める
「4時10分」は、ここから10分経ったときの両針の状態です。10分後にはどうなるでしょうか
変化量
図形的な考え方
120°離れた状態から、長針は10分で6×10=60°進み、短針は0.5×10=5°進みます。
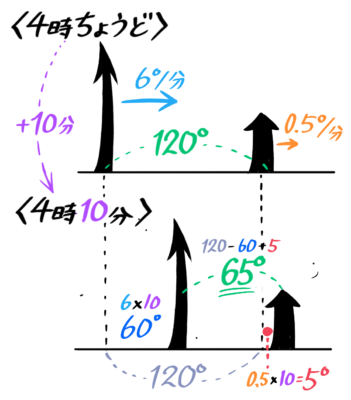
差し引き、長針と短針の間は120°–60°+5°=65°になると分かります。
変化量を使う考え方
もっと簡単な方法を紹介します。
両針の角度は1分で「角速度の差」5.5°ずつ縮まっていくので、10分では5.5×10=55°縮まります。
これで10分後の角度は、はじめの角度120°ー縮まった55°=65°になると分かります。
先程行った計算と中身は同じです。
120-60+5=120-(60-5)=120-55=120-5.5×10
重なる(追いつく)前と後
今度は4時30分の両針の角度を考えます。
4時ちょうどの120°から、30分で5.5×30=165°差が縮まります。
…あれ?と思った人は鋭いです
120°から165°差を縮めるのはやりすぎで、差を120°縮めた時点で角度は0°になります(両針が重なった状態)。
これは上で出した4時21911分の出来事です。
30分での変化量165°の残り45°は短針を追い越した長針が広げた差を意味します。
((図))
従って、4時30分の角度は45°になります。
このように「4時10分」と「4時30分」では考え方が少し異なります。その違いは「両針が重なる前か後か」で生じます。
→両針の重なる時刻がポイント
●両針が重なる前(例:4時10分)
→4時ちょうどの両針の角度120
→10分での角度の変化量55°
→120-55=65°(4:10の角度)
●両針が重なる後(例:4時30分)
→4時ちょうどの両針の角度120
→30分での角度の変化量165°
→165-120=45°(4:30の角度)
ある時刻(N時M分)の両針の角度を求める場合は、重なる前か後かを考えて下さい。
ここで、ある時刻(N時M分)の両針の角度の求め方をまとめるとこうなります。
●N時M分の角度
N時ちょうどの角度(30xN)°から(5.5xM)°変化する
○長針が追いつく前~(30xN)ー(5.5xM)
(例)4時10分の角度
→120°から5.5×10=55°変化する(追いつく)
→両針の角度は120-55=65°
○長針が追いついた後~(5.5xM)ー(30xN)
(例)4時30分
→120°から5.5×30=165°変化する(追いつき引き離す)
120°追いついて両針が重なり、さらに165-120=45°引き離す
→両針の角度は45°
一直線になる
長針と短針が一直線になる場合を考えます。
一直線になるというのは長針と短針の角度が180°になるということです
(図)
この問題も、上の「ある時刻の角度」と同じように長針が短針に「追いつく前に一直線になる場合」と「追いついた後に一直線になる場合」に分けて考えると理解しやすい
追いつく前に一直線になる場合
例1
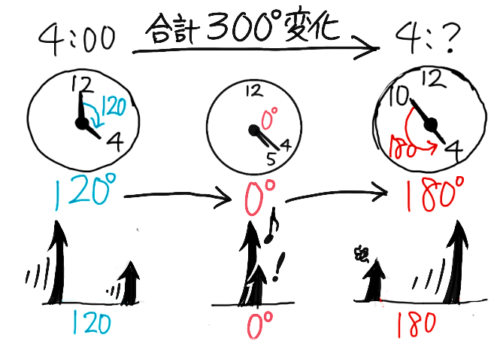
10時から11時までの間で両針が一直線になる時刻を求めなさい
10時の時点で両針の角度を考えるときは少し注意が必要で、後ろから長針が追いかけると考えて短針は300°前にいることになります。

ここから両針が一直線になる(180°になる)のには120°差を縮めればよい
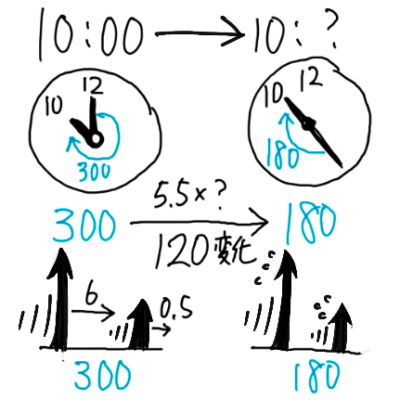
この状態から両針の角度は5.5°/分の割合で縮まっていくので、一直線になるのにかかる時間は120÷5.5=21911より、10時21911分になる。
確認テスト(作成中)
追いついた後に一直線になる場合
例題2
4時から5時までの間で両針が一直線になる時刻を求めなさい
4時の時点で短針は長針の120°前にいて(この図は見慣れたでしょうw)、この差は縮まるしかありません。
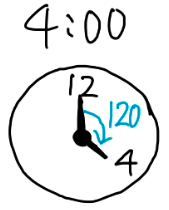
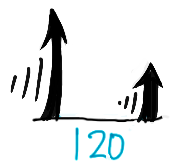
だから両針が一直線(180°)になるには、まず長針が短針に追いついてさらに180°差を広げないといけないので、両針の角度は120+180=300°変化することになります。
さらに180°まで広げないとダメなので
120+180=300°変化することになる
これにかかる時間は300÷5.5=54611なので、一直線になるのは4時54611分になる。
確認テスト(作成中)
小まとめ
追いつく前と後の分かれ目はN時での両針の角度が180°より大きいか小さいかです。
両針が一直線(180°)になる時刻
●N時の両針の角度P°が180°より大きい
→一直線になるのにかかる時間は(P–180)÷5.5
10時の角度は30×10=300°なので、
(300-180)÷5.5=10時21911分
●N時の両針の角度が180°より小さい
→1回追いついてから180°引き離す必要がある
→一直線になるのにかかる時間は(P+180)÷5.5
4時の角度は120°なので、
(120+180)÷5.5=4時54611分
直角になる
記事の見直し中です。申し訳ございません…
針の角度が直角(90°)になる場合も、一直線(180°)になる場合と同様に、追いつく前と後に分けて考えましょう。
追いつく前に直角になる
N時の角度が90°より大きい場合は、追いつく前に90°になります。
例えば10時から11時の間に90°になる時刻を考えます
始めの角度は300°で、ここから追いかけて角度90°に減れば良い
(図)
変化は300-90=210°なので210÷5.5=38211より、90°になるのは10時38211分です。
追いついた後に直角になる
一方、N時の角度が小さい場合は追いついたあとに直角になります。
例えば2時から3時の間に90°になる時刻を考える
2時の角度は60°で、ここから90°になるには、一度追いついて(0°にして)さらに90°の角度まで差を広げることになる
(図)
変化は60+90=150°なので150÷5.5=27311より、90°になるのは2時27311分です。
追いつく前と後に直角になる
実はもう1つの場合があるのです。
例えば4時から5時の間に90°になる時刻を考えます。
始めの角度は120°で、ここから追いかけて角度90°になれば良い
(図)
変化は120-90=30°なので30÷5.5=5511より、4時5511分に90°になります
(図)
この後、長針は短針との角度をどんどん広げていくので…もう1回90°になりますね!
(図)
この「2回目の90°」になるには、4時ちょうどの120°からは120+90=210°も変化したことになります
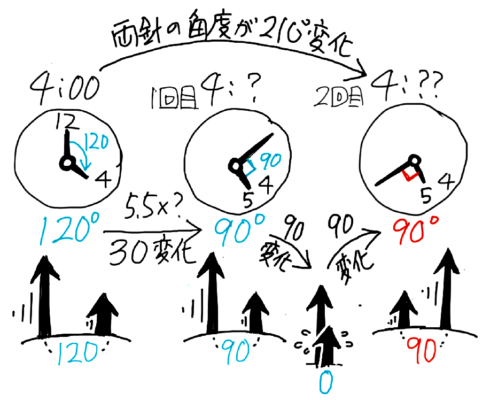
よって「2回目」の時刻は、210÷5.5=38211より、4時38211分とわかります。
答えは、4時5511分と4時38211分の2つです
(テストでは「全て(両方)求めよ」と「2回目を求めよ」がよく問われる)
確認テスト(作成中)
小まとめ
このように、両針が直角になる問題は3つタイプがあります。
図を書けば分かるので、「3つのタイプ」を無理に憶える必要はありませんが、まとめるとこうなります。
両針が直角(90°)になる時刻
●N時の両針の角度P°が90°より小さく
長針が短針の「後」にいる(12時~2時)
→追いついた後に1回直角になる
→(P+90)÷5.5分後
2時の角度は30×10=300°なので、
(300-180)÷5.5=10時21911分
●N時の両針の角度P°が90°以上(3時~9時)
→追いつく前と後の2回直角になる
→1回目は(P–90)÷5.5分後
→2回目は(P+90)÷5.5分後
2時の角度は30×10=300°なので、
(300-180)÷5.5=10時21911分
●N時の両針の角度P°が90°より小さく
長針が短針の「前」にいる(10時~11時)
→追いついた後に1回直角になる
→(P+90)÷5.5分後
→1回追いついてから180°引き離す必要がある
→一直線になるのにかかる時間は(P+180)÷5.5
4時の角度は120°なので、
(120+180)÷5.5=4時54611分
特定角度になる
その他の問題
時計以外の角速度を使う問題
オススメ教材
 爽茶
爽茶分かりやすい!と評判のスタディサプリにも時計算の授業動画がありますよ(6年応用の9回/10回)。今なら14日間無料。
興味がある人は「先取りや予習・復習に! スタディサプリ そうちゃ式のオススメ利用法」へ
●時計算周辺の問題を集中して解きたい場合は「旅人算・通過算・時計算・流水算」(グノーブル)
●その他の単元を合わせて予習復習をしたい場合、「算数の基本問題4年(日能研)」
●小6受験生には「算数ベストチェック」(日能研)
