「面積出せって言われても…何か変な形なんだけど…」とお困りの中学受験生の方、安心して下さい!
東大卒講師歴20年の図解講師「そうちゃ」が公式で求められない四角形の面積を求め方をまとめました。
記事を真似して問題を解けば、たいていの問題は解けるようになっているでしょう。
目次(クリックでジャンプ)
工夫が必要!
公式にない四角形(や五角形以上の多角形)の面積を出す場合は工夫をしないといけません(求積の工夫)。工夫の仕方にはいくつかあります。
A公式で出せる図形の和や差にする
B等積変形を使う
C.重なりを利用する
D.水平垂直を利用する
順番に見ていきます!
和や差に直して求める
工夫の1つ目は、公式で面積を出せる形の➀和 ➁差 に直す方法です。
(復習)四角形の分類と公式
和や差に直す以前の、四角形の基本を復習します。「憶えてるよ!」という人はジャンプして下さい。
四角形の分類
面積の公式
長方形の面積=縦の長さx横の長さ
平行四辺形の面積=底辺x高さ
台形の面積=(上底下底)x高さ÷2
ひし形の面積=対角線1x対角線2÷2
図形の和にして求める
五角形
長方形+直角三角形
下の図形です。
((長方形と斜辺で接する直角三角形))
五角形です。「五角形の面積」という公式は知らないので、このままでは解けません。
しかし線を引くと…長方形と直角三角形に分けられますね。
((線を引いた図))
面積は になります。
台形+直角三角形
下の図形です
((図形))
これも線を引けば…台形と直角三角形に分けられます
((線を引いた図形))
面積は になりますね。
確認テスト(2021.12.30作成中)
無名四辺形
こういう問題です。
((長方形+台形))
五角形なので当然公式は知りませんね。
でも落ち着いて線を引いて2つに分ければ…長方形と台形に分けることができますね。
((線を引いた図))
面積は になります。
確認テスト
長方形の中の斜線部
こういう問題です。この形は四角形ですが公式にはない形ですね。
((図))
直角に注目します。直角は「平行四辺形」「三角形」などで高さを見つけるヒント記号でしたね。
((平行四辺形・三角形の図))
長方形の直角を生かすように、こういう風に2つに分ければ三角形の公式を使って求められますね。
((分割した図))
どういう風に分ければよいか分からない!」という方のために、直角と底辺・高さのセットに色を付けてみました。
((分割した図色付き))
テストの時は色が付けられませんが、直角を延長してみれば分かりますよ!
確認テスト
対角が直角な四角形の中にある場合
こういう問題です。外側の図形は平行な二辺もない「ただの四角形」ですが…直角がありますね。
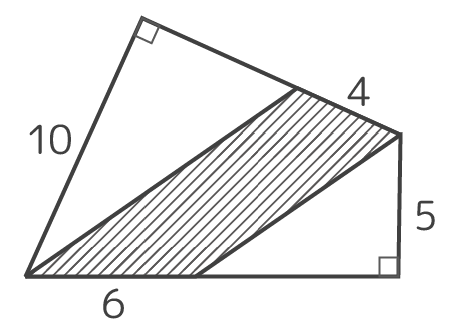
上でやったように直角を延長して見ましょう。
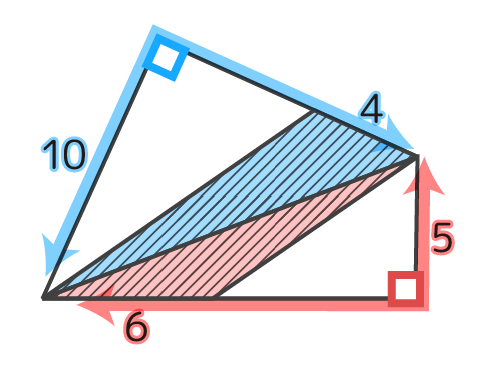
それぞれセットにすれば良いと分かる
これで底辺と高さのセットが分かるので、それが生かせる向きに四角形を分割します。
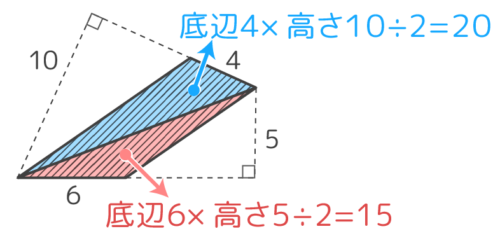
全部では20+15=35と分かります。
これで面積は35と分かります。
確認テスト
代表的な「和に直すタイプ」は以上です。
図形の差で出す
1つの図形を切り取る
こういう問題です。分かる人が多いのではないでしょうか?
斜線部は三角形ー三角形で求められますね。
2つ以上の図形を切り取る
切り取る形が示されていない場合
少し難しい問題です。何から何を切り取れば好いか分かりますか?
((直角二等辺-直角二等辺))
全体が直角二等辺三角形になるように補うと、切り取る部分も直角二等辺三角形になります!
((補助線を引いた状態図))
形は分かりましたが、三角形の底辺と高さが分かりません。
((??付きの図))
直角二等辺三角形は正方形の半分で、正方形はひし形でもありました。
対角線が分かればひし形(正方形)の面積が出せるので、直角三角形の面積も求められます。
((図))
これで面積は と分かりますね。
確認テスト
等積変形を使う
等積変形の方法
例題
道の変形
基本パターン
クロス型
複合形
等積変形の応用
重なる図形
重なる等積図形
面積が等しい図形が重なると、重ならない部分の面積も等しくなります
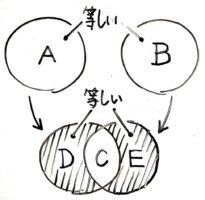
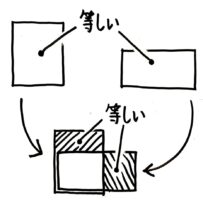
例題
3-1:等積重複図形
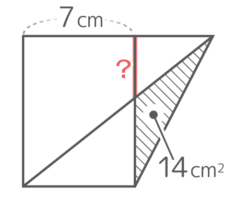 長方形と三角形、直線からなる図形があります。斜線部の面積が14cm2のとき「?」は何cmですか?
長方形と三角形、直線からなる図形があります。斜線部の面積が14cm2のとき「?」は何cmですか?「?の部分を一部とする図形が欲しい!」と思えれば、長方形に対角線を引いて三角形を作れるかも
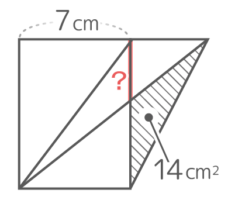
すると三角形の等積変形の図が出来ます。面積が等しい図形の重なっていますね
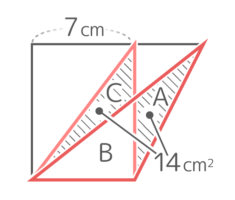
等積図形の重ならない部分は等しいので、A=C=14cm2です。
三角形としてのCの高さは7cmで底辺が?cmなので、?x7÷2=14 を逆算して?=4cm です
練習問題(2020.6.23作成中)
重なる図形の差
面積が等しくない図形が重なる場合、重ならない部分の差は元の2つの図形の差と等しくなります。
例えば、面積80と面積45の図形を重ねたら、重ねた部分が25だっとします
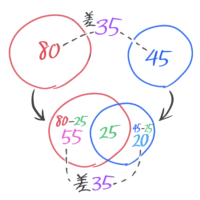
すると、重ならない部分の面積差も35になっていますね
これを使った問題を解いてみます。
3-2-1:重なる図形の面積
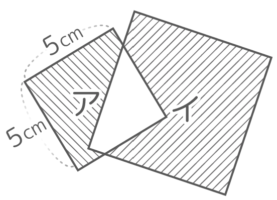 2つの正方形が重なっていて、小さな正方形の1辺は5cm。アの部分の面積がイの部分の面積より24cm2大きいとき、大きな正方形の1辺は何cmか
2つの正方形が重なっていて、小さな正方形の1辺は5cm。アの部分の面積がイの部分の面積より24cm2大きいとき、大きな正方形の1辺は何cmか

次の問題はもう少し図形らしく問題を解きましょう
3-2-2:重なる図形の面積
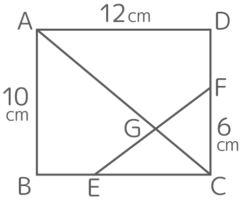 図において、四角形AGFDと三角形GECの面積の差は36cm2です。ECの長さを求めなさい
図において、四角形AGFDと三角形GECの面積の差は36cm2です。ECの長さを求めなさい色を付けてみると、赤は青より36cm2小さいということです。
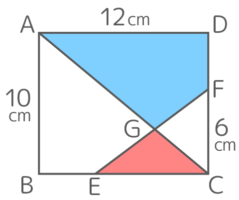
ここでACD(青+紫)とECF(赤+紫)が重なっていると考えると、
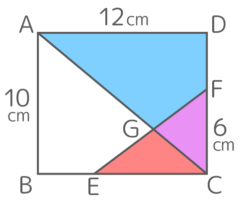
重なっていない部分(赤と青)の差が36なので、

元の図形ACD(青+紫)とECF(赤+紫)の差も36cm2と分かります。
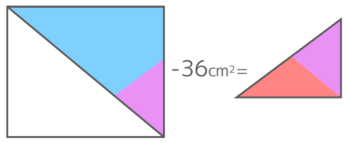
そしてACD(青+紫)の面積は長方形で60cm2なので、ECF(赤+紫)の面積は24cm2と分かります
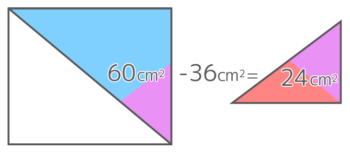
ECF(赤+紫)の高さは6cmで底辺ECが?なので、?x6÷2=24 を逆算して、?=8cmになります。
水平垂直の利用
方眼上にある場合
方眼ノートを使っている人も多いでしょう。
方眼の上に図形が描かれた問題では方眼を利用して和や差を作って解きます。
例えばこういう問題です。
確認テスト
水平垂直に分割
基本問題
応用
上のように水平垂直に分割したときに全部の長さが分からない場合は難しくなります。
こういう問題や
X-1
 斜線部の面積を求めなさい
斜線部の面積を求めなさいこういう問題です
X-2
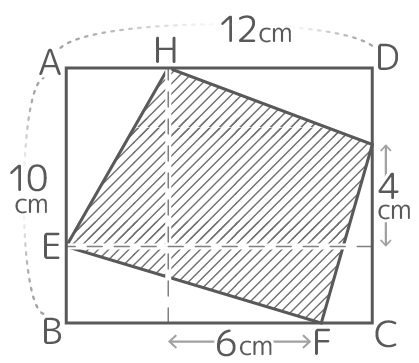
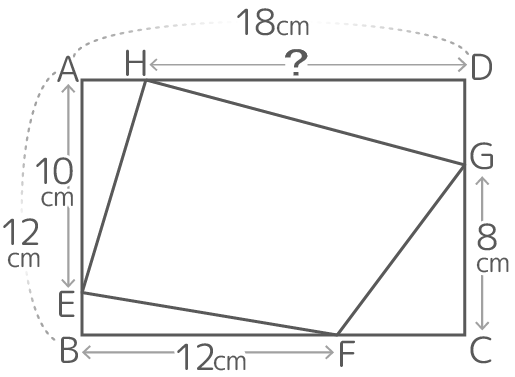 □EFGH=135cm2のとき、HDは何cmか?
□EFGH=135cm2のとき、HDは何cmか?いきなり答えを出すのは難しいので、順を追って解きましょう♪
全体・外堀・内堀の関係
前提として、このような図形の各部分がどのような関係にあるかを理解して下さい
一番外側にある長方形を「全体」、長方形より少し小さい四角形を「外堀」、内側にある小さな長方形を「内堀」として(お城の構造に例えています)、「全体」「外堀」「内堀」の関係を理解して下さい
内堀の辺を外堀まで上手に伸ばすと、全体と内堀の間が4つの長方形に区切られて、それらを外堀が2等分してる図ができます。
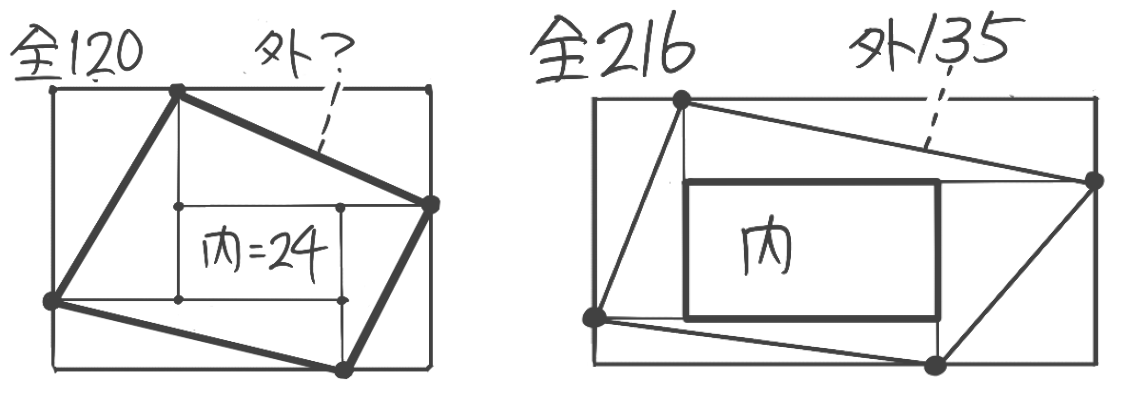
問題1は「全体」と「内堀」から「外堀」を出す問題で
問題2は「全体」と「外堀」から「内堀」を出す問題です
この関係を頭に入れて、もう一度問題を見てみましょう
解法を理解
X-1:水平垂直応用
 斜線部の面積を求めなさい
斜線部の面積を求めなさい解説
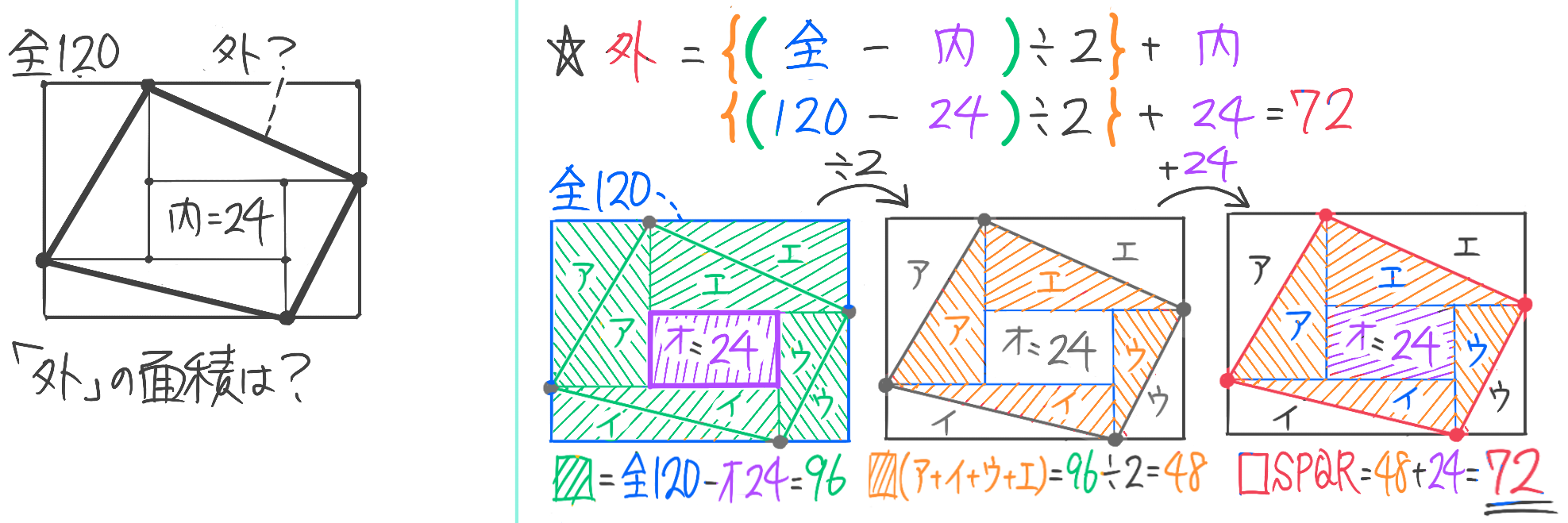
全体の面積120で、内堀の面積が6×4=24と気づけば上の練習と全く同じです。
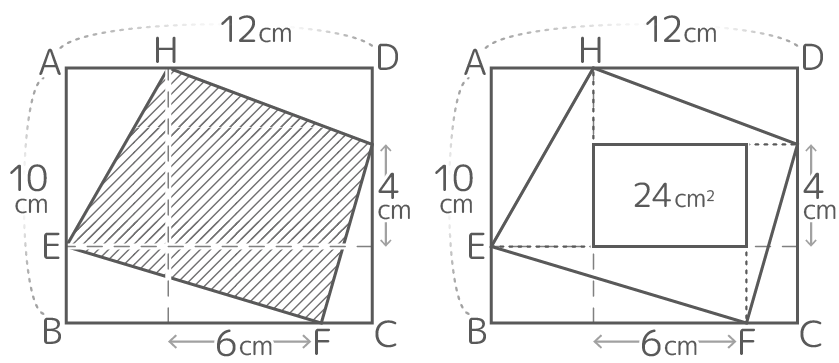
斜線部(外堀)={(120(全体)-24(内堀))÷2}+24(内堀)=72cm2
次の問題
X-2:水平垂直応用
 □EFGH=135cm2のとき、HDは何cmか?
□EFGH=135cm2のとき、HDは何cmか?解説
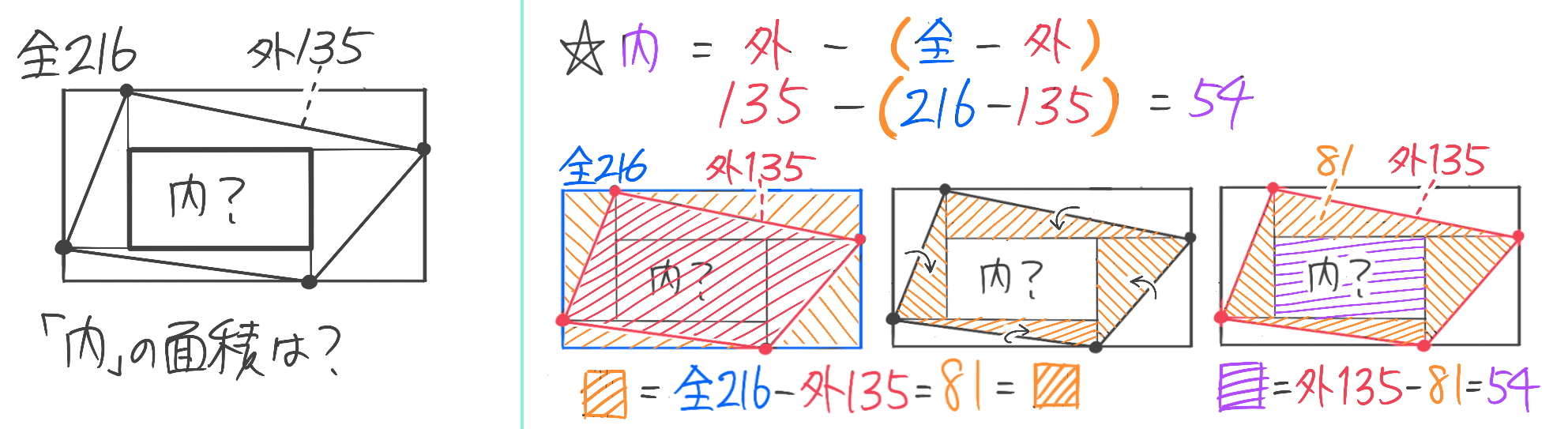
HDを求めるには、内堀の面積を求める必要がありますが、そこは上の練習と全く同じです。
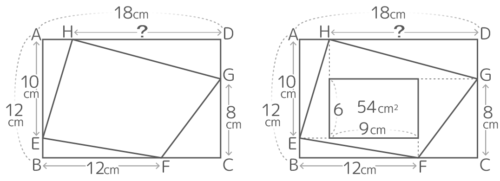
内堀の面積=135(外堀)-(216(全体)-135(外堀))=54cm2
内堀の縦の長さ=(10+8)-12=6なので、内堀の面積=54から内堀の横の長さ=54÷6=9cmと分かります
分かりましたね?
次のステップへ
 爽茶
爽茶オリジナル教材のご案内
御三家・早慶付属など難関・人気の中学に合格した2025年度の受験生達から大好評!
分かりやすいのはもちろん、スキマ時間にお子様一人で反復定着できますよ
人気教材はこちら(クリックするとショップ内教材ページにジャンプ)
●歴史 ●時事問題(2025年) ●世界地図 ●世界遺産
■仕事ニュートン算 ■食塩水 ■売買損益
★月の形 ★電流 ★水溶液/気体の性質
その他にも社会/理科/算数の教材がございます。興味がある方は公式ストアへどうぞ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
 爽茶
爽茶「中学受験と高校受験とどちらがいいの?」「塾の選び方は?」「途中から塾に入っても大丈夫?」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。
