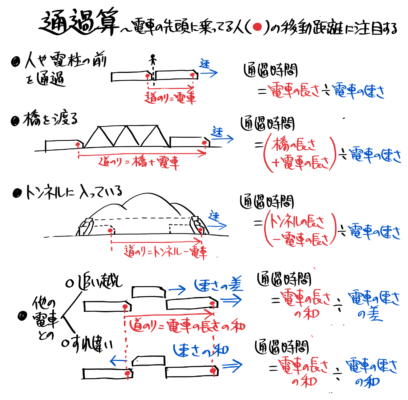
「通過算がよく分からない…」という中学受験生の方へ
確かに電車とか鉄橋とかトンネルとか…いろんな長さのものが出てきてゴチャゴチャしてますが…
実は「コツ」をたった1つ憶えるだけで通過算は簡単になるんですよ！本当に「1つ」だけです！
この記事では、東大卒講師歴20年の図解講師「そうちゃ」がコツを使った解き方をわかりやすく説明します
記事を読んで真似すれば通過算が好き/得意になっているかも！？
速さ(復習)
爽茶こんにちは！「そうちゃ」@zky_tutor(プロフィール)です。
通過算の前に、速さをサッと復習します。「分かるよ！」という方はジャンプして下さい。
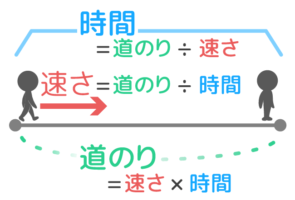
速さの公式
速さの公式をパッと言えるようにしておきましょう
覚え方のコツは「『道のり』だけがかけ算」「残りは『道のり÷』」というように「道のり」だけを覚えることです。
①道のり=速さ×時間
②速さ=道のり÷時間
③時間=道のり÷速さ
速さの単位
通過算は「m/秒」で答えを出すことが多いので、もし問題文に書いてある速さが「km/時」だった時は、単位を変えないといけません。
速さの単位は時間と距離2つを含んでいるので少し面倒でした
◆単位時間
大きくする(→)と速さは60倍
小さくする(←)と速さは160倍
◇距離の単位
大きくする(↓)と100または1000倍
小さくする(↑)と1100または11000倍
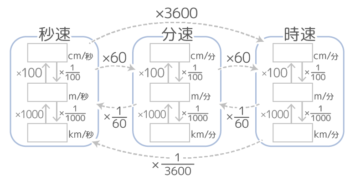
例えば108km/時をm/秒に直す場合、まず3600で割って(←←)km/秒に直し、次に1000倍してm/秒に直します。
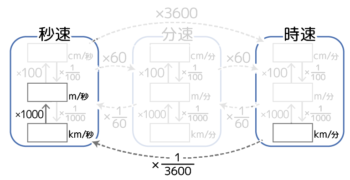
実際の計算は、分数の式にして1回で済ませます。
108km/時=108÷3600×1000=108×10003600=30m/秒
旅人算の公式
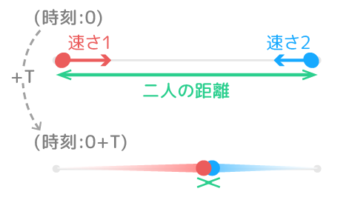
移動している2人が「出会う」「追いつく」2つの場合がありました。時間(T)を求める公式を思い出して下さい。
❶出会う時間(T)=2人の距離÷速さの和
②2人の距離=速さの和×出会う時間
③速さの和=2人の距離÷出会う時間
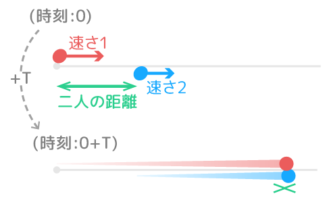
❶出会う時間(T)=2人の距離÷速さの差
②2人の距離=速さの差×出会う時間
③速さの差=2人の距離÷出会う時間
では、通過算を始めましょう
一点を通過する
「通過算」は電車のように長さがあるものが「何か」を通過するのにかかる時間です。
はじめに、電車が電柱や人のように長さが無いモノの前を通過するのにかかる時間を考えます。
考え方を理解
1-1:立っている人の前を通過
解説
まず「通り過ぎる」とはどういうことか考えるために図を書きましょう。
Aさんの前に列車の先端がさしかかった瞬間と後端がAさんの前を過ぎた瞬間を図にするとこうなります。
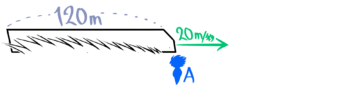
「通過するのにかかる時間」は図1の状態から図2の状態になるまでの時間のことです。
そして、時間を求めるので「時間=道のり÷速さ」の式を使います。速さは20m/秒で良いでしょう。
では、「道のり」に使う長さは何でしょうか？図をみてもよくわかりませんね…
ここで、電車の中でBさんが一番先頭車両の一番前に立っているとします(自分が電車を操縦している気分になれる♪)
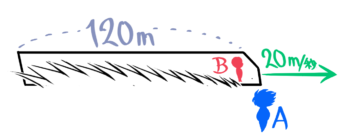
Bさんを含めて図1と図2を重ねるとこうなります。
通過する時の電車の移動距離=電車の長さ
と分かります
電車全体ではなく一点(B)を見れば、図1から図2になる間に電車が動いた距離が分かります。この長さを道のりとして公式を作れば良いのです。
「電車の中の人が動いた距離を書く」これが通過算の最大のコツです！
そしてBさんが動いた距離はちょうど列車の長さと同じになっていますね！
したがって、通過するのにかかる時間は
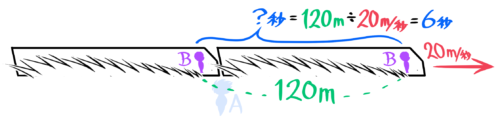
列車の長さ120m÷列車の速さ20m/秒=6秒 と分かります
このように、人や電柱など一点の前を通り過ぎるのにかかる時間は「電車の長さ÷電車の速さ」で求められます。
速さの三公式のように「長さ(道のり)=」「速さ=」「時間=」の形にまとめるとこうなります(全部を暗記する必要はありません。最低限「時間=」を言えるようにして下さい)。
電柱や人など一点を通過する場合
★電車の先頭にいる人が動いた長さに注目
●通過時間=列車の長さ÷列車の速さ
(例)長さ120m速さ20m/秒の列車が人の前を通過
→通過時間=120÷20=6秒
(図)
○列車の長さ=列車の速さ×通過時間
○列車の速さ=列車の長さ÷通過時間
類題で定着
1-1:立っている人の前を通過
解説
通過時間＝電車の長さ÷速さ なので、120m÷4秒=30m/秒
解説
今度の列車の長さは、120m×1.5=180m で、この距離を12秒で通過したことになるから、
列車の速さは 180m÷12秒=15m/秒 と分かる。
もっと問題を解きたい人は、記事の下の「オススメ教材」を見て下さい。
長さを通過する
先程は一点(電柱や人)を通過するのにかかる時間を考えましたが、今度は鉄橋やトンネルのような長さがあるものを通過する時間を考えます。
鉄橋(トンネル)を通過する
考え方を理解
鉄橋を通過する場合も、さっきと同じように電車の先頭に乗っている人の移動距離を考えます。
2-1:鉄橋を通過
解説
電車が橋にさしかかった瞬間と橋を渡り終わった瞬間を図にするとこうなります(鉄橋を渡るときに「ゴ～～」と音がなりますね。あの音が鳴り始めてからなり終わるまでです。)
(図1と図2を合わせた図 Bなし)
ここに電車の先頭に立つのが大好きなBさんと移動距離を書き込むとこうなります。
(Bありの図 赤い線分)
赤い長さは、電車の長さ(120m)＋鉄橋の長さ(300m)=420mになっています。これが電車の移動距離になります。
(Bありの図 数値)
したがって、電車が鉄橋を通過するのにかかる時間は、420÷20＝21秒になります。
ちなみに、トンネルを通過する場合も同じです
(長さ300mのトンネルの場合の図 Bさん 数値付き)
このように、橋やトンネル等長さがあるモノを通過するのにかかる時間は、(電車の長さ+橋やトンネルの長さ)÷電車の速さ で求められます
速さの三公式に対応してまとめるとこうなります。(全部を暗記する必要はありません。通過時間は言えるようにして下さい)
橋やトンネルなど長さがあるモノを通過する場合
★電車の先頭にいる人が動いた長さに注目
●通過時間=(列車の長さ+橋の長さ)÷列車の速さ
(例)長さ120m速さ20m/秒の列車が300mの鉄橋を通過
→通過時間=(120+300)÷20=21秒
○列車の長さ=(列車の速さ×通過時間)-橋の長さ
○橋の長さ=(列車の速さ×通過時間)-列車の長さ
○列車の速さ=(列車の長さ+橋の長さ)÷通過時間
類題で定着
2-1:トンネル・橋を通過
解説
通過する際の移動距離(道のり)は80+170=250m
これを移動するのに10秒かかったので、列車の速さは250ｍ÷10秒=25m/秒
解説
通過する際の列車の移動距離は25×6=150mで、これは電車の長さ(80m)と鉄橋の長さの和
したがって、鉄橋の長さ=150-80=70ｍ
もっと問題を解きたい人は、記事の下の「オススメ教材」を見て下さい。
トンネルの「中にいる」時間
条件が少し変わります。
考え方を理解
2-2:トンネルに隠れている
解説
通過するのと違うのが分かりますか？図を書くとこうなります。
(図)
「隠れている」のはトンネルの中に最後尾が隠れた瞬間から、トンネルの外に先頭が顔を出す瞬間までで、先頭に乗っているBさんを書き足すと移動距離はトンネルの長さ(280m)-電車の長さ(100m)= 180mと分かります。
(図 B 赤い線分)
したがって、トンネルの中に隠れているのは180÷20=9秒間です。
「トンネルの中に隠れる」だけでなく「電車全体が橋の上にある」なども同様の図と計算になります
一応、公式にしておきます。図の書き方・考え方の例として憶えても良いでしょう。
電車全体がトンネルの中に隠れている時間を求める
★電車の先頭にいる人が動いた長さに注目
●隠れている時間=(トンネルの長さー列車の長さ)÷列車の速さ
(例)長さ100m速さ20m/秒の列車が280mのトンネルを通過
→隠れている時間=(280ー100)÷20=9秒
類題で定着
(2021.11.16作成中)
2つのモノを通過する「時間差」の問題
少し応用的な問題です
2-3:時間差の問題
ヒント
Aさんとホームを同時に通過し始めるように、Aさんの立ち位置を調整
解説
Aさんにホームの端に立ってもらい、電車がホームとAを通過し始める瞬間(X)、Aさんの前を通過した瞬間(Y)、ホームを通過した瞬間(Z)を図にして、電車の中に(おなじみ)Bさんも書き込むとこうなります。
ホーム全体を通過するのに16秒かかる
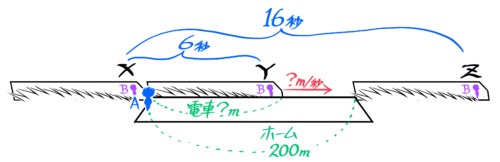
Aさんの前を通過し終わってからホーム全体を通過し終えるのに16-6=10秒かかっていて、この間の電車(Bさん)の移動距離はちょうどホームと同じ200mなのが分かります！
ホーム全体を通過するのに16秒かかる
ホーム長200mと同じと分かる
したがって、電車の速さは200÷10＝20m/秒と求められます
解説
駅員の前を通過するのにかかる時間が6秒で、速さが20m/秒と分かったので、電車の長さは20×6=120mです。
もう一問やってみましょう。
2-4:時間差の問題
ヒント
鉄橋とトンネルを並行な線路に並べて、同時に通過し始めるようにすれば…
解説
同じ長さ同じ速度の電車が2台並んで走っていて、鉄橋とトンネルを同時に通過し始めると考えます。
トンネルと鉄橋を通過し始める瞬間、鉄橋を通過し終わる瞬間、トンネルを通過し終わる瞬間と電車(Bさん)の移動距離、所要時間を図にします。
(図)
すると、480m-300m=180mを32-23=9秒で移動したと分かります！
したがって、列車の速さは180÷9=20m/秒です。
また、300mの鉄橋を渡るのに23秒かかっているので、(電車の長さ+300m)÷20m/秒=23秒 という式を逆算で解けば電車の長さが求められます。
電車の長さ=(23×20)-300=160ｍと分かります。
もっと問題を解きたい人は、記事の下の「オススメ教材」を見て下さい。
追い越す・すれ違う
次は、電車が動くモノとすれ違ったり追い越したりするのにかかる時間を考えます。
旅人算の出会い・追いつきを思い出して下さい。追いつく場合は2つの速さをマイナスして、出会う場合は2つの速さをプラスしました。
あれと同様に、追い越す場合は2つの速さをマイナスし、すれ違う場合はプラスすれば良いのです。
車(自転車)とすれ違う
考え方を理解
3-1:自転車とすれ違う
解説
2つの動いているモノの絵を書くときは、1つを「固定」して残りの1つだけが動いていると考えます。
この問題では自転車を固定して、電車だけを動かします。
(開始と終了の図 B 赤い線分)
これですれ違う時に移動する距離は電車の長さに等しいと分かりますが、この図での電車の速さは25m/秒ではありません。
すれ違うので自転車の速さ5m/秒とプラスされて30m/秒と考えないといけません(25m/秒だと止まっている人の前を通過することになります)
(開始と終了の図 電車に相対速度を書く)
したがって、すれ違いにかかる時間は、電車の長さ(120m)÷電車と自転車の速さの和(30m/秒)で4秒になります
類題
作成中(2021.11.16)
他の電車とすれ違う
自転車ではなく他の電車とすれ違う場合はどうなるでしょうか
考え方を理解
3-2:他の電車とすれ違う
解説
また、一方を固定して図を書きます。ここではQを固定して書くと、すれ違いの際のPの移動距離は2つの電車の和(120+160=280m)と分かります。
(図 B 赤い線分)
そして2つの電車の速さがプラスされることを考えると、Pは25+15=40m/秒の速さでQとすれ違うことになります。
(全部入りの図)
したがって、すれ違いにかかる時間は、電車の長さの和(280m)÷電車の速さの和(40m/秒)で7秒と分かります
このように、二台の電車がすれ違うのにかかる時間は「長さの和÷速さの和」になります。
●電車が他の電車とすれ違う場合
→2つの速さはプラスされる
すれ違う時間=(電車の長さの和)÷(電車の速さの和)
(例)長さ120m速さ25m/秒の列車Pと
長さ160m速さ15m/秒の列車Qがすれ違う場合
→すれ違う時間=(120+160)÷(25+15)=7秒
類題で定着
作成中2021.11.16
もっと問題を解きたい人は、下にある「オススメ教材」を見て下さい。
車(自転車)を追い越す
今度は追い越しです
考え方を理解
3-3:自転車を追い越す
解説
ここでも自転車を固定して、電車だけを動かす図を書きます。
(開始と終了の図 B 赤い線分)
すれ違う時に電車が移動する距離は電車の長さで、追い越しなので自転車の速さ5m/秒を電車の速さ25m/秒からマイナスして20m/秒と考えます。
(開始と終了の図 電車に相対速度を書く)
したがって、追い越しにかかる時間は、電車の長さ(120m)÷電車と自転車の速さの差(20m/秒)で6秒になります
類題
作成中(2021.11.16)
他の電車を追い越す
3-4:電車を追い越す
解説
またまた一方を固定して図を書きます。Qを固定して書くと、追い越しの際のPの移動距離は2つの電車の和(120+160=280m)と分かります。
(図 B 赤い線分)
そして2つの電車の速さがマイナスされることを考えると、Pは25-15=10m/秒の速さで(ゆっくりと)Qを追い越すことになります(電車に乗ったことがあれば分かるでしょう)。
(全部入りの図)
したがって、追い越しにかかる時間は、電車の長さの和(280m)÷電車の速さの差(10m/秒)で28秒と分かります
このように、電車が他の電車を追い越すのにかかる時間は「長さの和÷速さの差」になります。
二台の電車のすれ違いと追い越しをまとめると、こうなります。
(例)長さ120m速さ25m/秒の列車Pと
長さ160m速さ15m/秒の列車Qを考える
●電車が他の電車とすれ違う場合
→2つの速さはプラスされる
すれ違う時間=(電車の長さの和)÷(電車の速さの和)
(例)列車Pと列車Qがすれ違う場合
→すれ違う時間=(120+160)÷(25+15)=7秒
●電車が他の電車を追い越す場合
→2つの速さはマイナスされる
追い越し時間=(電車の長さの和)÷(電車の速さの差)
(例)列車Pが列車Qを追い越す
→追い越し時間=(120+160)÷(25–15)=28秒
類題で定着
作成中2021.11.16
もっと問題を解きたい人は、下にある「オススメ教材」を見て下さい。
おすすめ教材
爽茶オススメの問題集
●通過算だけを練習したい人にサイパーシリーズから「通過算」が登場♪
●受験算数を総復習したい小6には、コンパクトな「算数ベストチェック」(日能研)や解説が厚い「塾技100 算数」(文英堂)
が良いですよ♪
●算数や図形が苦手な人には、ほどよい解説もある「算数の基本問題 6年」(日能研)が良いですね♪
「分かりやすい！」と評判の
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。