多角形とは
基本的な図形のうち、(直線状の)辺と頂点のみで出来ている図形です。
簡単に考えると、「円」や「おうぎ形」のような曲線がある図形を除いた図形です
今まで学習してきた「三角形」「(正)(長)方形」「四角形(台形・平行四辺形・ひし形)」はもちろん多角形です。
それ以外にも五角形・六角形や
((図))
星型や、言い表せない形(自己交叉多角形)などがあります。
((図))
多角形の角度
内角
このように、N角形の内角の和は180×(N-2)です。
外角
このように、多角形の外角の和は角の数(N)に関係なく常に360°です。
多角形の対角線
対角線
対角線は、ある角と別の角を結んだ線です。
((対角線の例))
但し、隣り合う角とは作れません。辺になってしまいます。
((ダメな例))
対角線の本数の公式
四角形、五角形くらいなら対角線の本数は数えれば分かりますね
((四角形五角形の対角線の図))
四角形では2本、五角形では5本あります。
しかし、十角形や十二角形の対角線となると数えるのはちょっと無理
((十角形・十二角形の対角線の図))
そこで、N角形の対角線の本数を公式にしてみましょう。
数え方
例えば五角形の場合、一つの頂点から自分と両隣の3点以外つまり5-3=2点に向けて対角線を引けます
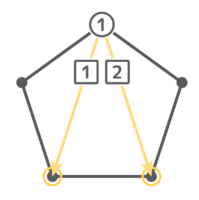
同様に他の頂点からも2本づつ対角線を引けるので
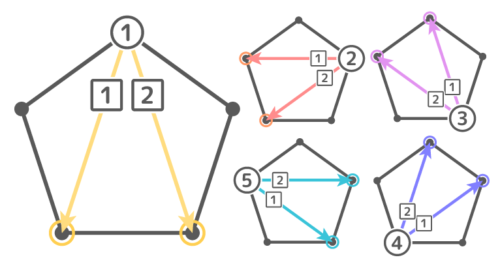
合計2×5=10本の線が引けますが…合わせてみると
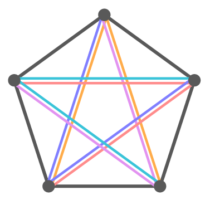
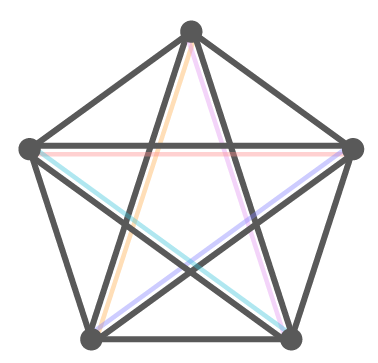
同じ線を2回づつ引いているのが分かります。
よって最後に÷2しないといけません。
結局、五角形の対角線は(5-3)×5÷2で5本となりました。
自分と両隣の3点以外の2点に線を引く
引いているので
5本になる
公式化
このように、N角形の対角線の本数は N×(N-3)÷2 で求められる
N角形の対角線の本数＝N×(N-3)÷2 本
(理由)
それぞれの頂点N個から
自分と両隣の3点以外の(N-3)個の頂点に線を引き
2回ずつ数えているので÷2する
(例1)5角形の場合～5×(5–3)÷2=5本
(例2)10角形の場合～10×(10–3)÷2=35本
多角形の分割
面積が等しい部分に分けてみる
三角形
方形
平行四辺形
六角形
六角形の分割は入試でよく出るので、受験生は小4の間に憶えて書けるようにしておきましょう
ニ等分
三等分
六等分
それ以上
十二等分や十八等分があります。
((図))
星形多角形
角度を求める問題です。
解法
三角形を利用
外角を利用
組み合わせ
交叉型の星形
オススメ教材
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。