「旅人算に比が出てくるとワケわかんない(泣)」という中学受験生の方へ。
その気持、よく分かります！「旅人算」だけでも複雑なのに、さらに難しい「速さと比」まで加わったら…ワケわかんないのも当然
正直、「旅人算と比」は中学受験で一番難しい分野だと思います。前提となる事柄が「速さ」「旅人算」「比」「速さと比」等と多く、しかも1年以内にドドドｯと押し寄せてくるので理解定着のヒマがありません
ただ「速さと比」は(中堅以上の中学の)入試に出てくるので、最低でも基本問題は解けるようにしておくべきです
そこでこの記事では、東大卒講師歴20年の図解講師「そうちゃ」が「速さと比」を前提になる事項から分かりやすく説明します。
記事を読んで例題を解けば「速さと比」の基礎が身につくでしょう。
目次をクリックすると読みたい箇所にジャンプできます。
目次(クリックでジャンプ)
前提になる事柄
「旅人算と比」は中学受験の算数で一番難しい分野だと思います。
その理由は、前提となる色々な事柄をマスターしていないと「旅人算と比」を理解すらできなからです。
そこで前提となる事柄を確認します。
旅人算
動く人が2人以上いる場合が旅人算の問題で、大きく分けて「出会い」と「追いつき」がある。
直線上の旅人算
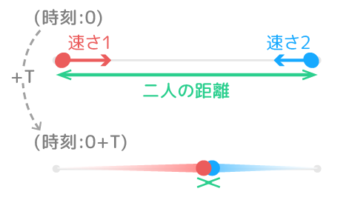
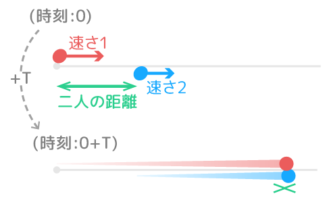
公式
❶出会う時間=2人の距離÷速さの和
②2人の距離=速さの和×出会う時間
③速さの和=2人の距離÷出会う時間
❶出会う時間=2人の距離÷速さの差
②2人の距離=速さの差×出会う時間
③速さの差=2人の距離÷出会う時間
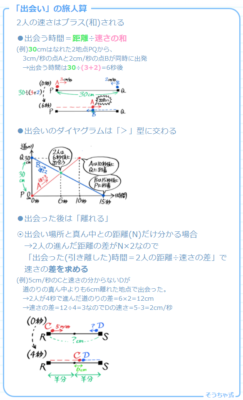
小まとめ
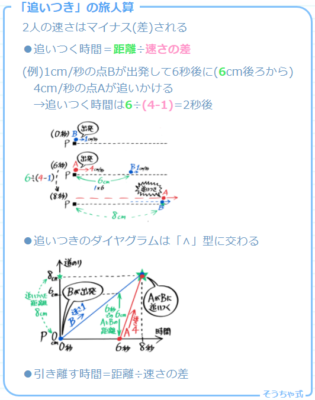
円周上の旅人算
1回目の出会い・追い付きは直線に直して計算し、出会いや追い付きの「周期」を求めます。
2回目以降の出会い・追い付きは「周期」を使ってときます。
比
速さと比
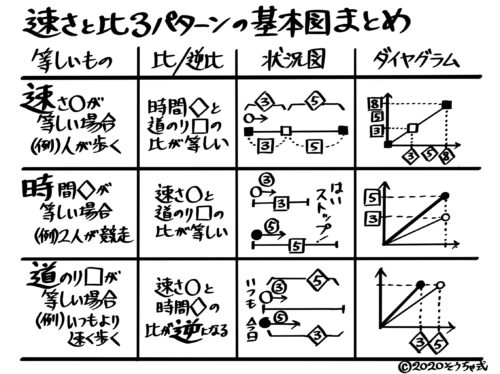
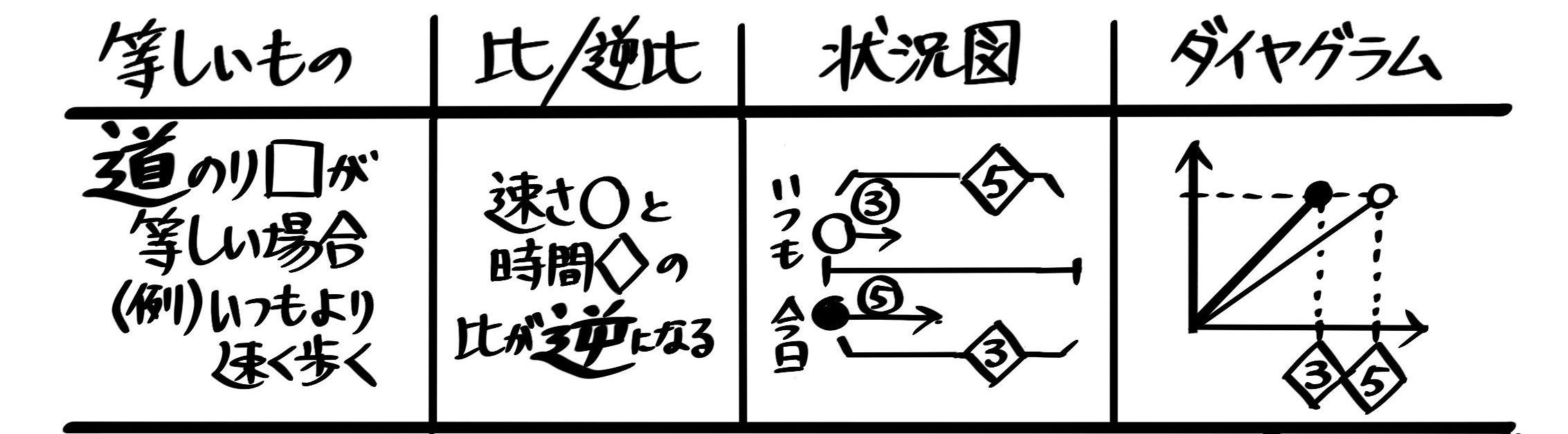
2つの場合を比べます。
2つの場合で速さが同じ場合→時間が倍になると進む道のりも倍になる(時間の比=道のりの比)
2つの場合で時間が同じ場合→速さが倍になると進む道のりも倍になる(速さの比=道のりの比)
2つの場合で道のりが同じ場合→速さが倍になるとかかる時間は半分倍になる(速さの比と時間の比は逆)
前提となる事柄の確認が終了したので、いよいよ「旅人算と比」を始めます。
直線上の旅人算と比
まず直線上の旅人算と比です。
出会う場合
例えば「速さ3:5のAとBが2地点XとYから向かい合って同時に出発します。二人は12分後に出会い、その後もYとXに到着するまで進む」場合を考えます。
出会うまで
AB2人は出発してから出会うまで進む時間は等しいので、これは「速さと比」の”時間が等しい”パターンです。
つまりAとBが進む道のりの比は速さと同じ3:5になるので、XY間を3:5に分ける地点(Z)で出会います。XY全体は8になります。
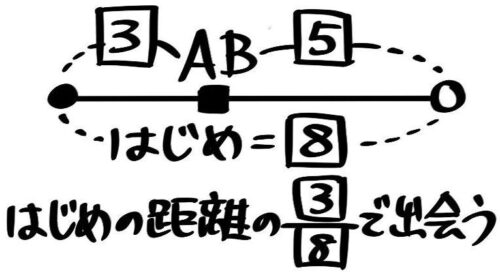
出会ってから
一度出会った後はABどちらか一方の行動に注目し、さっき分かった3:5を使っていろいろな時間を明らかにします。
Aに注目
Aに注目すると、AはXを出発して全体の38のZでBと出会い、その後残り58を進んでYに到着します。
これは「速さと比」の”速さが等しい”場合なので、XZ:YZの道のりの比とかかる時間の比が等しくなります。
かかる時間の比は道のりと同じくも3:5になり、3=12分なので、5＝20分と分かります。
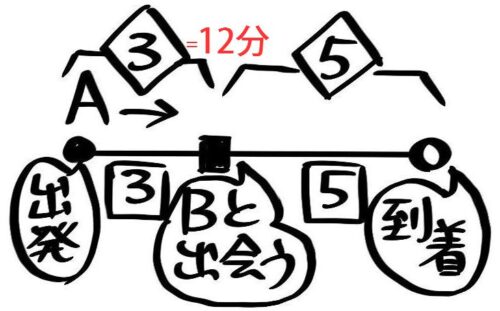
向こうにつくまでの時間=5
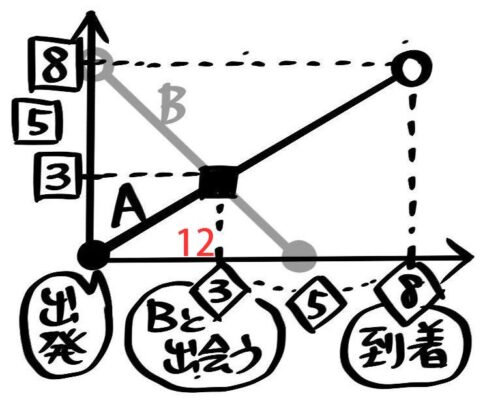
結局、AはXを出発して12分後にZでBと出会いその20分後(出発から32分後)にYに着くと分かりました。
Bに注目
Bに注目すると、BはYを出発して全体の58のZでAと出会い、その後残り3/8を進んでAに到着します。
かかる時間の比は道のりと同じく5:3になり、5=12分なので、3＝7.2分と分かります。
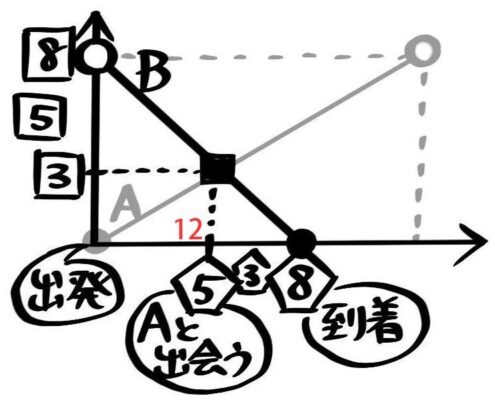
結局、BはYを出発して12分後にZでAと出会いその7.2分後(出発から19.2分後)にYに着くと分かります
追いつく場合
例えば、
追いつくまで
追いついてから
Aに注目
Bに注目
ダイヤグラムの利用
分からないことが多い場合(特に速さの比が分からない場合)は状況図を書いても解くのが難しいです。
ダイヤグラムを書き、相似の図形問題として解くと簡単に解けることが多いです。
Z-1:ダイヤグラムの利用
(解説)
兄と弟の速さの比も時間の比も分かりません…
このような時はとりあえずダイヤグラムを書いてみます。
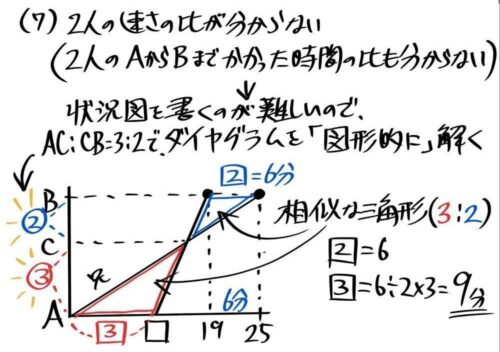
ダイヤグラム上に出来る「2:3の砂時計型の相似」を出来ていることに気付きます。
これを利用すると、兄と弟の出発の時間差3の値が9分と分かります。
ちなみに、状況図を丁寧に書いても解けますが、正直、面倒くさいです。
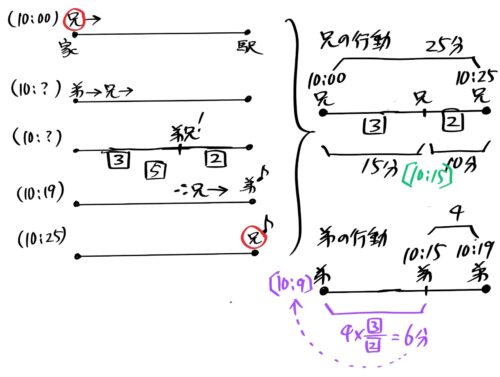
問題文を読んで「？」が頭をよぎったら、迷わずダイヤグラムを書きましょう！
円周上の旅人算と比
考え方
(比の無い)円周上の旅人算と同様に考えます。
1回目の出会い追い付きは直線に直して計算し「周期」を出して、2回目以降の出会い追い付きは「周期」を使って求めます。
円周旅人算(出会い)と比
2-1:旅人算(円周出会い)と比
解説
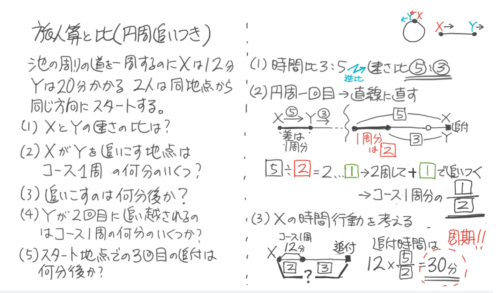
まず直線に直して「出会いの周期」を出します。
等しい距離を進むのにかかる時間の比が28:21=4:3なので、速さの比は逆比で③:④になる。
解説
1回目の出会いなので直線に直して考える。また出会いは「時間が等しいパターン」であることを思い出す。
直線上の2人の時間が等しいパターンの図を書くと、XとYがそれぞれ3:4進んだ地点で出会う。これはXからみると全体の37になる。
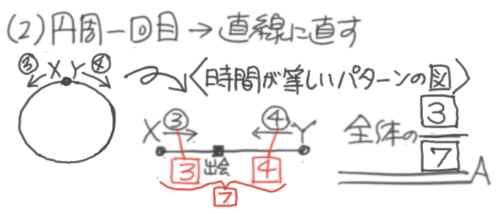
解説
Xの行動に注目する。
一周回るのに28分かかっているので、一周の37にあたるスタートから出会い地点までは28×37=12分かかると分かる。
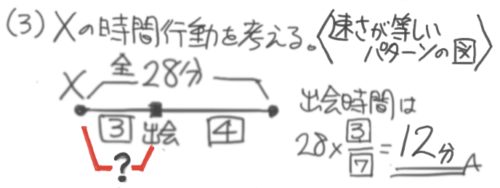
周期の利用
ここまでで分かった事をまとめます。
●2人は12分ごとに出会う。これが出会い時間の周期
●Xは一周の37、Yは一周の47進むたびに出会う。これが出会い場所の周期
この先はこの「周期」を利用します。
解説
遅い方、ここではXに注目する。
最初の出会いから2回目の出会いまでに全体の37進む。
これが600mにあたるから、一周は600÷37=1400mと分かる。
解説
Xは3進むごとにYと出会い、一周は7なので、3と7の最小公倍数21進むとちょうどスタート地点でYと出会う。
Xは一周7を進むのに28分かかるので、㉑を進むのには28×217=84分かかる。
確認テスト
作成中
円周旅人算(追い付き)と比
確認テスト
作成中
円周上の異なる点から出発する問題
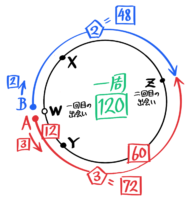
2人が円周上の異なる点から出発して2回出会うまでの様子から2人の速さや一周するのにかかる時間を求めるこんな問題です。
Z-3:異なる点から出発
円周上に反時計回りに点X,Y,Zがある。AはXからYに向かって、BはYからXに向かって一周する。同時に出発したところ、2人は6分後に初めて出会った。AはBと出会ってから4分後にYを通過し、その20分後にZでBと再び出会った。以下の問いに答えなさい。
速さの比が分かったら、それを使って各地点間の距離を仮に求めてしまうのがコツです。
Z-3:異なる点から出発
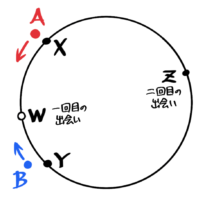
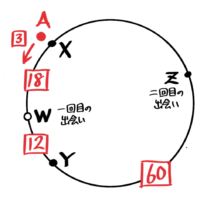
(解説)
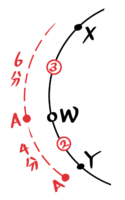
1回目の出会いまでのAの行動を追うと、XからBと出会う点(Wとする)まで6分、WからYまで4分なので、XW:WY=③:②と分かります。
XWとWYの長さの比が3:2と分かる
そして出会うまでの6分でAとBが進んだ距離の比もXW:WY=③:②なので、AとBの速さの比も3:2と分かります。
AとBの速さも3:2と分かる
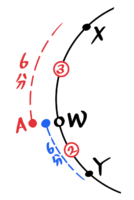
(解説)
Aの速さを3として距離を計算すると、XW=3×6=18、WY=3×4=12、YZ=3×20=60となります。
XW,WY,YZの長さを出してしまう
一回目の出会いから2回目の出会いまでに2人が進む道のりは3:2です。
出会うまでの距離も3:2
AはWYZの12+60=72(または3×24=72)の距離を進んでいるので、この間にBは2/3の48の距離を進みます。
これで一周の距離が72+48=120と分かります。
一周は120となる
よってAが一周するのには120÷3=40分,Bが一周するのには120÷2=60分と求められます。
確認テスト(2021.3.21作成中)
往復の旅人算と比
お知らせ
新4年生の方を対象に学習相談/授業を実施します(1次募集はサピックス新越谷校の方のみ対象。締め切り1/23)。応募はコチラから
おしらせ
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。