中学受験生で「すい」の問題が苦手という方へ
確かに立体図形はイメージする力が必要なので苦手に感じる人は多いのですが、中学受験で出題される立体図形は「柱」と「すい」だけ。
5年までに「柱」と「すい」の基本を完璧にすれば、あとは入試に間に合うように応用をじっくりと練習すればOKです。
この記事では「すい」の性質から応用問題まで東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。
記事を読んで例題がスラスラ解けるまで練習すれば、「すい」を含めた立体図形全体が苦手ではなくなっているでしょう
「すい」の性質
すい体の構成と名称
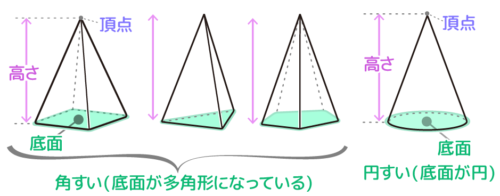
下の形(底面)から底面の真上にある一点に向かってとがる形の立体が「すい体(錘)」です
底面から頂点までを垂直に測った距離がすいの「高さ」です(体積を出すときに使います)
(角すいの場合は別の組合わせの頂点と底面を考えることもできます。)
すいの名前は底面の形で決まります。
底面が円なら「円すい」
三角形なら「三角すい」
四角形なら「四角すい」
底面が多角形の場合は、まとめて「角すい」とも呼びます。
底面以外の、周りを取り囲む面を「側面そくめん」と呼ぶ。
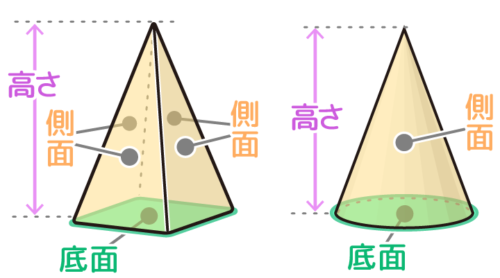
角すいはいくつかの側面をもちますが、円すいは一つの側面しかもちません。
角すいの場合、方体や角柱と同じように頂点・辺・面の個数を数えられるようにしておきましょ
X-1:角すいの構成要素
解説
頂点は底面に4個+頂上に1個=5個
辺は底面に4本+側面にも4本=8本
面は底面1面+側面4面=5面
ヒント
四角すいの計算を変えれば良いですね
解説
頂点は底面に6個+頂上に1個=7個
辺は底面に6本+側面にも6本=12本
面は底面1面+側面6面=7面
すい体の体積
「すい」は底面積が同じ「柱」の1/3の体積になります。(詳しい説明が読みたい人は下をクリック)
1辺1cm(体積1cm3)の立方体を「一つの面(正方形)を底面積とする四角すい」に切り分けると、同じ形が6個できます。
この四角すいの体積は1cm3の立方体を6等分したものなので、16cm3になります。
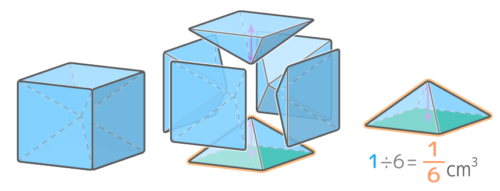
そしてこの四角すいの底面は正方形(1cm2)で高さは12cmなので、底面が同じ柱の体積は1×12cm=12cm3になります。
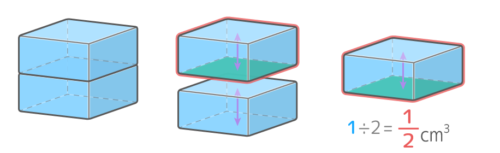
底面積と高さが同じ四角すいと四角柱を比べると、すいが16cm3で、柱が12cm3なので、すいは柱の13になっているのがわかります♪
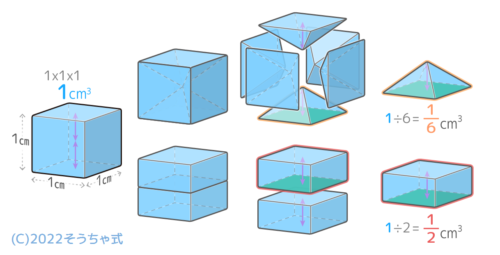
「柱」の13の体積になっている
柱の体積=底面積×高さ」だったので、「すいの体積=底面積×高さ×13」になります。
=柱の体積の13=底面積×高さ×13
すい体の展開図
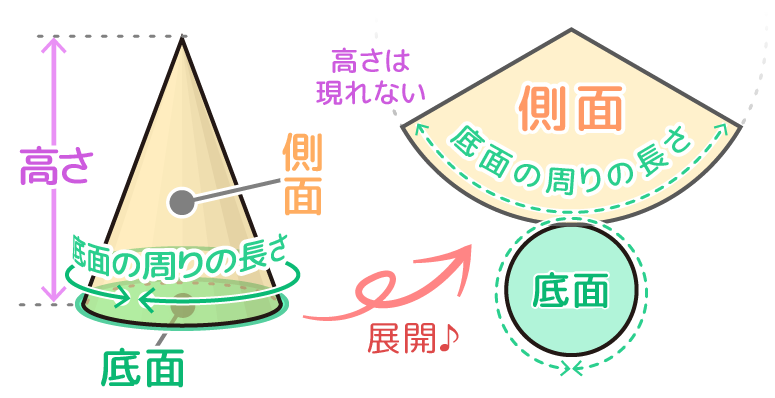
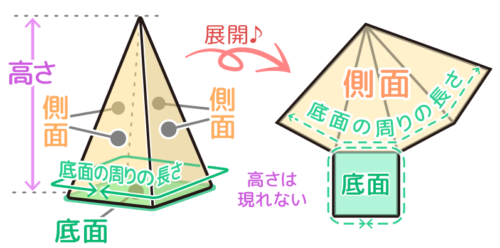
(実は何種類も作れますが)底面をはずし、側面を開いた展開図が基本です
この時、底面のまわりの長さと側面の一部が同じ長さになっています。
そして「高さ」は展開図には現れません
角すいは多角形の底面と三角形を組み合わせた形の側面に展開でき、側面の一部(三角形の底辺の合計部分)は底面積の周りの長さと等しくなります。
円すいの場合は、円形の底面とおうぎ形の側面に展開されます。おうぎ形の孤の部分は底面の円の周長と等しくなります。
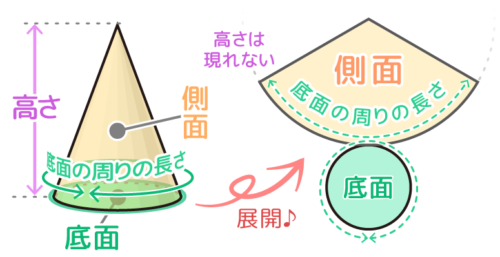
このおうぎ形の半径や中心角については、後で詳しく説明します。
すいの表面積
すいの展開図が1つの底面と1つの側面になると考えるので、
すいの表面積=底面積+側面積
と考えることができます。ちなみに
柱の表面積=底面積×2+側面積
でした。
小まとめ
●すい体=底面からとがる立体
→底面の形で名前が決まる
●構成～一つの底面と側面を持つ。
角すいは側面3つ以上、円すいは1つ
●展開すると1つの底面と1つの側面ができる。
円すいの側面はおうぎ形になる
●すいの計量
○すいの体積=底面積×高さ×13
○すいの表面積=底面積+側面積
円すいの性質と計量
円すいの3つの長さ
円すいは、円形の「底面」から底面中心の真上にある「頂点」に向かってとがる形の立体です。
底面の円の「半径」と底面から頂点までの「高さ」の2つの長さ(これらは体積を求める時に使います)以外にも重要な長さがあります
それは頂点から底面の円周に引いた最短距離で、これを「母線ぼせん」と呼びます(表面積を出すのに使います)
この「半径・高さ・母線」のトリオが円すいで重要な数字です。
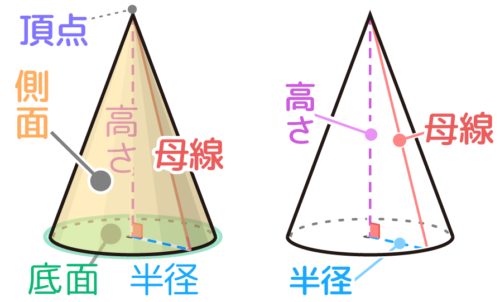
直角三角形を作っている
「半径」「高さ」「母線」の3つは直角三角形を作っている。
この直角三角形は、円すいを頂点で垂直に切ったときの切り口の半分になっている。(「回転体」で使います)
円すいの体積
すいの体積=柱の体積×13=底面積×高さ×13でした。
たがって、円すいの体積は底面積が同じ円柱の13になるので、
円柱の体積の公式 「(底面の半径×半径×3.14)×高さ」の最後に「×13」をつけて
円すいの体積=(底面の半径×半径×3.14)×高さ×13となります。
=(底面の半径×半径×3.14)×高さ×13
例えば、下図のような円すいの場合
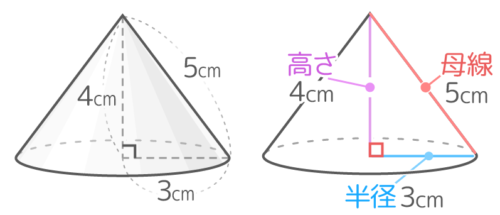
半径,母線,高さに注目
半径=3,高さは4なので、体積=(3×3×3.14)×4×13=12×3.14=37.68となります。
3.14の筆算はできるだけまとめて1回だけ行いましょう。
確認テスト
円すいの展開図
上で見た円すいをもう一度使います。
これを切り開いて展開図にすると、底面(円)と側面(扇形)の2つのパーツになります。柱と違い底面は1つだけです
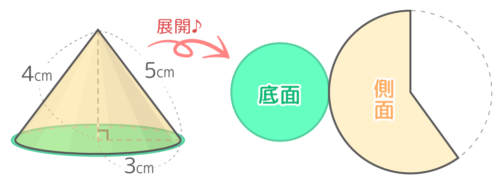
この展開図に「半径」「母線」とそれらから導ける長さを書き込むとこうなります(高さは展開図には現れない)
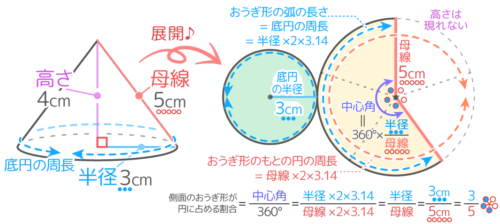
元の円の周長=母線を半径とする円周
展開図だけを拡大すると…
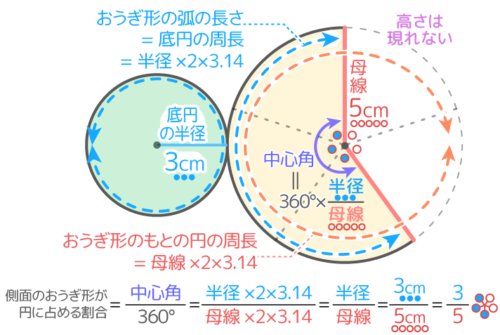
底面(円)
半径3cmの円
側面(おうぎ形)
円すいの母線5cmを半径とするおうぎ形
側面の中心角
中心角を出すために、このおうぎ形が(母線を半径とする)もとの円にしめる割合(=中心角360)を考える
結論から言うとおうぎ形がもとの円に占める割合(=中心角360)は半径母線となる(途中をみたい人は下をクリック)
この割合はおうぎ形の弧おうぎ形のもとになる円の周長と等しく、また展開図を組み立てることを考えると、おうぎ形の弧は底円の周長と等しくなる
よって、おうぎ形がもとの円に占める割合=底円の周長もとの円の周長と分かる。
さらに、底面の円周=半径×2×3.14で、おうぎ形のもとの円の周長=母線×2×3.14なので…以上全てをまとめて、さらに計算(約分)すると
おうぎ形がもとの円に占める割合(中心角360)
||
おうぎ形の弧もとの円の周長
||
底円の周長もとの円の周長
||
底円の半径×2×3.14母線×2×3.14
||
半径母線
となって結局、おうぎ形がもとの円に占める割合は半径母線になる♪
例の円すいの場合は35になる(5つの○のうち3つが●になっているのが分かります)
底円の周長もとの円の周長=半径母線=35であるのに注目
この半径母線は円すい関連で一番大事な数でしょう
「おうぎ形の中心角＝360°×おうぎ形が円に占める割合」なので、円すいの場合は
側面のおうぎ形の中心角=360×半径母線という公式ができる
例の円すいの場合、中心角は360×35=216°になる。
→底面(円)が1つと側面(おうぎ形)が1つ
●底面は円
●側面は母線を半径とするおうぎ形
(もとの円にしめる割合は中心角360=半径母線)
○側面のおうぎ形の中心角
=360×半径母線
確認テストをどうぞ
半径が4、高さが3の円すいを展開図にした時、側面の扇形の中心角は？→( 円すいの断面の半分が「3:4:5の直角三角形」になるので母線が5になると分かる。側面のおうぎ形の中心角=360×45=288° )
円すいの表面積
「すいの表面積=底面積+側面積」でした。
円すいを展開してできる2つのパート(底円、側面のおうぎ形)の足し算になります。
底面積は「半径×半径×3.14」で良いですね
そして側面積はおうぎ形なので単純に考えると「母線×母線×3.14×中心角360」になりますが、
円すいの場合、この中心角360は半径母線と等しいので「母線×母線×3.14×中心角360」は「母線×母線×3.14×半径母線」と書き換えられます。
この「母線×母線×3.14×半径母線」の母線を約分した「半径×母線×3.14」が側面積になります(すごく単純になりました♪)
以上を合わせると
円すいの表面積=(半径×半径×3.14)+(半径×母線×3.14)
になるのですね
＝底面積+側面積
＝(半径×半径×3.14)+(半径×母線×3.14)
例の場合は、(3×3×3.14)+(3×5×3.14)=(9+15)×3.14=24×3.14=75.36cm2
ここでも3.14の計算は一回だけにしましょう。
確認テスト(作成中)
円すいの定理と公式まとめ
●円すいの構成=半径、高さ、母線の直角三角形
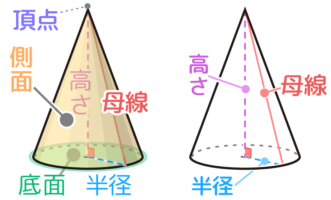
●円すいの体積=円柱の13
=(半径×半径×3.14)×高さ×13
●円すいの展開図
～底面(円)と側面(母線を半径とするおうぎ形)
○側面(おうぎ形)が円にしめる割合=半径母線
→おうぎ形の中心角=360°×半径母線
●円すいの表面積=底面積+側面積
=(半径×半径×3.14)+(母線×母線×3.14×中心角360)
=(半×半×3.14)+(母×母×3.14×半径母線)
=(半×半×3.14)+(半×母×3.14)
公式だけを取り出すと、こんな感じ
●体積=(半径×半径×3.14)×高さ×13
●表面積=(半径×半径×3.14)+(半径×母線×3.14)
●側面のおうぎ形の中心角=360°×半径母線
(例)半径3,高さ4,母線5の円すい
→体積=(3×3×3.14)×4×13=12×3.14=37.68
表面積＝(3×3×3.14)+(3×5×3.14)
=24×3.14=75.36
側面のおうぎ形の中心角=360×35=216°
角すいの性質と計量
角すいの展開図
一般的な展開図
特殊な角すいの展開図
正方形になる場合(後述)を覚えておく
角すいの体積
すいの体積の公式「底面積×高さ×13」で求められます。
底面積は簡単に求められることが多いのですが、高さははっきり示されていない場合は分からないことも多いです。
角すいの表面積
一般的な角すい
底面は簡単に分かることが多いが、側面積がよく分からないことが多い。
「3:4:5」「5:12:13」などの特殊な数値を使っている場合は求められる。
特殊な角すい
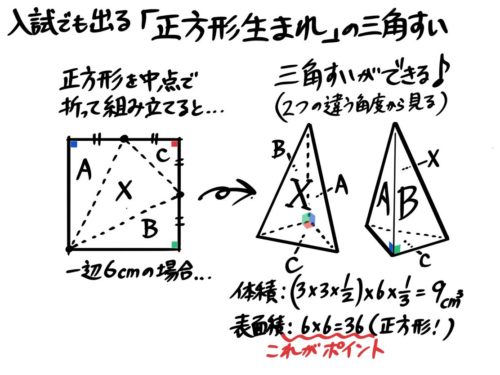
正方形のうち隣り合う二辺の中点を結んだ線と同じ対角にそれぞれ引いた線を折り目にして組み立てると
なんと三角すいができるのですね。
この三角すいの表面積は、当然正方形の面積そのものなので簡単に求められます。
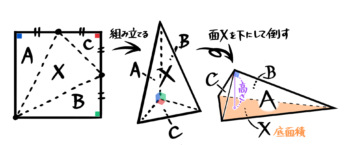
利用問題1(斜面Xの面積)
地面に対して斜めになっている面(X)の面積を求める問題です。もともと正方形からできているので、正方形の面積からABCの面積を引けばよいですね。
図の場合、正方形の面積が6×6=36、A=B=3×6÷2=9、C=3×3÷2=92なので、C=36-(9+9+92)=272と分かります。
利用問題2(斜面Xと対する頂点との距離)
入試でよく出るのが「面Xを底面とした時の高さ」や「面ABCが集まる点から面Xに垂直に下ろした線の長さ」です(２つとも同じ長さを聞いています)
例1で面Xの面積が272と分かりました。
そして、面Xを底面とした場合の高さを？とすると、体積はどこを底面にしても9cm3で変わらないので、「体積＝底面積×高さ×13」の公式を作ると
9=272×？×13 という式が出来ます。
これを逆算で解いて、?=2 と分かります!
利用問題3(角すい台)
立方体を切断して、この角すいそのもの、あるいは半分の高さで地面と平行に切った下半分(角すい台)を作り、体積や表面積を求める問題。
地面と水平・垂直な面は地道に計算してもよいですが、斜面Xは「相似比と面積比」を使わないと出せません。
例えば半分の高さで切った角すい台の場合、斜面は高さ(長さ)12の上の部分がもとのXの12×12=14倍の大きさなので、下の部分はXの34倍になります。
利用問題4(内接する球)
これは高校受験大学受験の問題ですが、小学生でも解ける問題です。
この角すいをABCXを底面とする三角すい4つに切り分けると、それら三角すいの高さは内接する球の半径Rに等しくなります。
4つのうちの1つ、Aを底面とする切り分けられた三角すいの体積はA×R×1/3になります。
((図がほしいところ…))
したがって、9(もとの角すいの体積)＝(A×R×1/3)+(B×R×1/3)+(C×R×1/3)+(D×R×1/3)=(A+B+C+D)×R×1/3 という関係が出来ます。
式を書き直すと、9=(A+B+C+D)×R×1/3 でA+B+C+Dは表面積なので何度も出てきた36です。
つまり 9=36×R×1/3 です。この逆算を解いて、R=3/4 と分かりますね！
すいの加工体
柱すい加工体
歴史の点数を上げたい受験生と保護者の方へ
年表・年号・地図・書き取りテストなど400枚のプリントがセットになった歴史教材で模試入試対策♪ 興味がある方はコチラへ
2023年度生徒さん募集
2023年度の生徒さんの募集を開始しました(対面授業の一次募集)
東武野田線・伊勢崎線沿線にお住まいの新5年生で予習シリーズをベースにされている方が対象です。
詳しくはコチラのページを御覧下さい
「図解サービスforSAPIX」のお知らせ
新4年生の方を対象に学習相談/授業を実施します(サピックス新越谷校・南浦和校・大宮校の方が対象。締め切り2/1)。応募はコチラから
中学受験でお悩みの方へ
爽茶「中学受験と高校受験とどちらがいいの？」「塾の選び方は？」「途中から塾に入っても大丈夫？」「塾の成績・クラスが下がった…」「志望校の過去問が出来ない…」など
様々なお悩みへのアドバイスを記事にまとめたので参考にして下さい。